Соединение в треугольник

Соединение источника и приемника треугольником изображено на рис. 12.

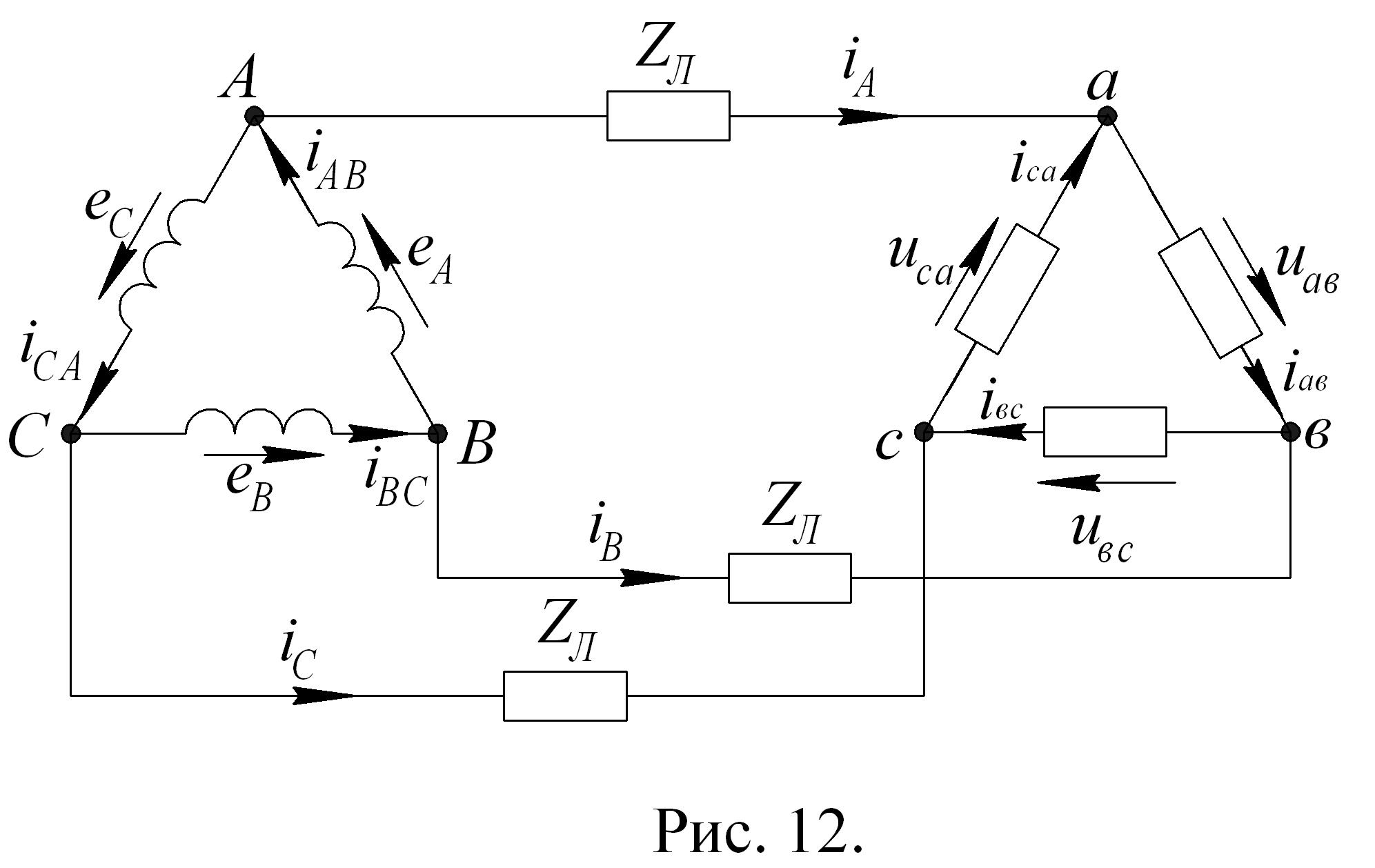
Положительным направлением ЭДС и токов источника считается направление от концов фазных обмоток к их началам (по обходу треугольника против часовой стрелки). Напряжения и токи приемника и напряжения источника направлены от начала каждой фазы к ее концу (т.е. по часовой стрелке). При соединении треугольником линейные и фазные напряжения одинаковы . Линейные токи направлены от источника к приемнику и, как видно из схемы рис. 12, определяются через фазные токи в соответствии с первым законом Кирхгофа следующими выражениями:

При симметричной нагрузке

Векторная диаграмма напряжения источника строится по известному фазному (линейному) напряжению в виде равностороннего треугольника (рис. 13).

Если сопротивления линейных проводов считать равными нулю, то векторная диаграмма напряжений приемника будет одинаковой с векторной диаграммой источника.

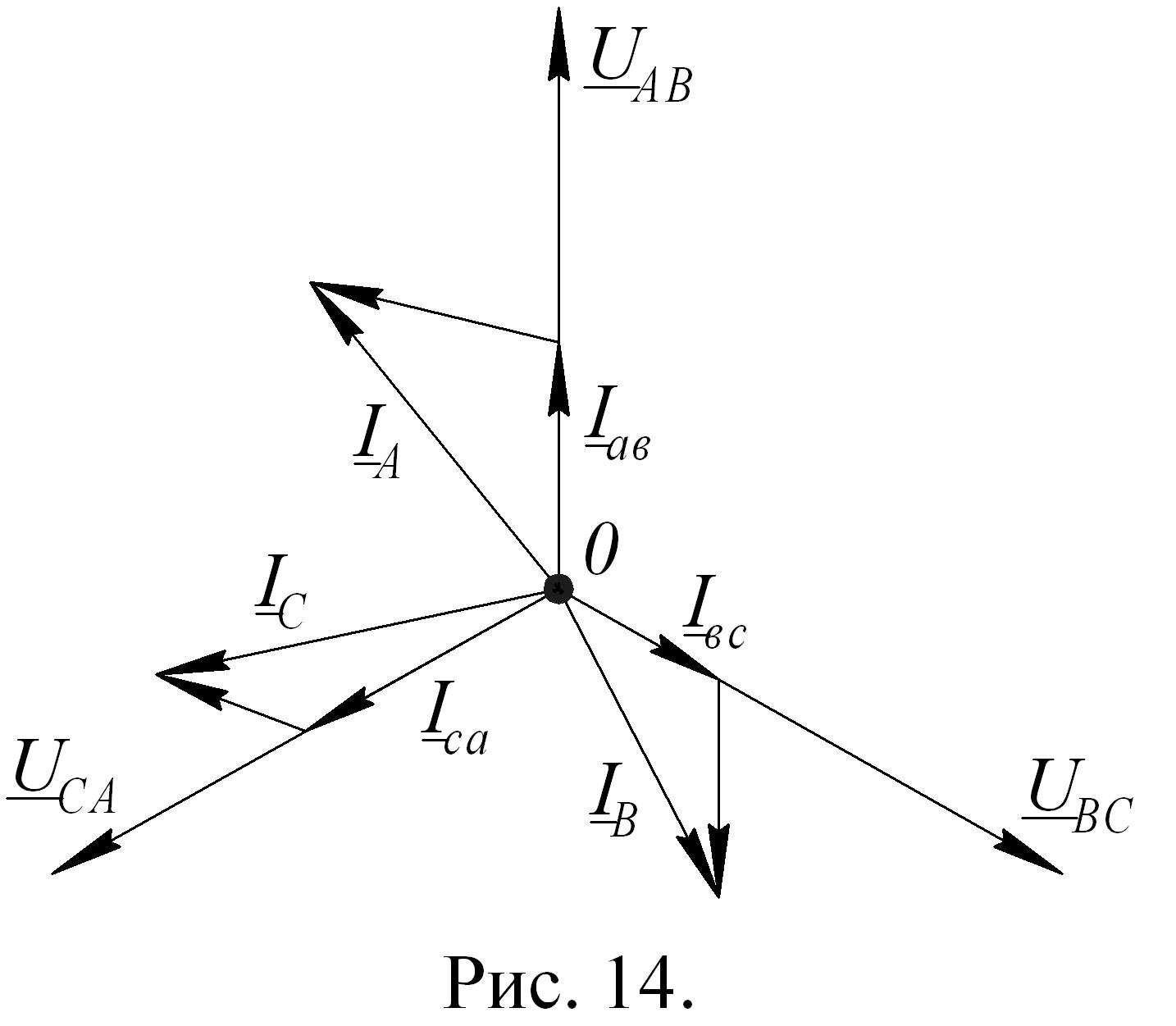
Для построения векторной диаграммы токов удобнее фазные напряжения приемника изобразить в виде звезды, сохраняя при этом сдвиг фаз напряжений. Векторы фазных токов приемника откладывают от точки 0 (рис. 14) с соответствующими сдвигами по фазе относительно фазных напряжений. Тогда линейные токи определяются, согласно первому закону Кирхгофа, векторами , , . При активном характере нагрузки векторы фазных токов совпадают по фазе с соответствующими фазными напряжениями.

Активная, реактивная и полная мощность трехфазной системы

Активной мощностью трехфазной системы называется сумма активных мощностей всех фаз приемника.

В симметричной трехфазной системе (при симметричном генераторе и приемнике) при любой схеме их соединений для каждой фазы мощности источника энергии и приемника одинаковы. Для каждой из фаз справедливо выражение

,

где - φ угол сдвига фаз между фазными напряжением и током.

Активная мощность системы в этом случае

Заменив действующее значение фазных тока и напряжения линейными при соединении источника энергии и приемника по схеме звезда т треугольник, получим одно и то же выражение для активной мощности симметричной трехфазной системы:

В общем случае реактивной мощностью трехфазной системы называется сумма реактивных мощностей всех фаз источника энергии, равная сумме реактивных мощностей всех фаз приемника.

Реактивная мощность симметричной трехфазной системы

,

или после замены действующих значений фазных тока и напряжения линейными

.

Комплексной мощностью трехфазной системы называется сумма комплексных мощностей всех фаз источника энергии, равная сумме комплексных мощностей всех фаз приемника. Полная мощность симметричной трехфазной системы

.

Трехфазные цепи с несколькими приемниками в симметричном режиме

Расчет трехфазной цепи в симметричном режиме сводится к расчету одной фазы и проводится аналогично расчету обычной цепи синусоидального тока.

Пример

Дано: - линейное напряжение;

- сопротивление линии;

- фазное сопротивление нагрузки 1;

- фазное сопротивление нагрузки 2.

Последовательность расчета:

1. Сопротивление двух треугольников, соединенных параллельно, необходимо заменить эквивалентным треугольником с сопротивлением фаз:

2. Полученный эквивалентный треугольник следует заменить эквивалентной звездой с сопротивлением фаз:

3. Определяют фазные сопротивления эквивалентной звезды с учетом :

4. Дальнейший расчет не требует применения комплексного метода. Достаточно определить действующее значение линейного тока

затем найти действующие значения фазного напряжения эквивалентной звезды приемника

и линейного напряжения приемника

.

Действующие значения фазных токов приемников определяются по закону Ома:

, .

Мгновенные значения симметричной системы фазных ЭДС выражаются аналитически следующим образом:

; ; .

Здесь начальная фаза ЭДС фазы (цепи) А принята равной нулю. В комплексной форме для действующих значений имеем:

E_А = E_A = E_Ф; E_B = E_Ae ^j240= E_фа²; E_С = E_Ae ^j120= E_фа,

где а = е^j120 – фазный множитель.

Алгебраическая сумма ЭДС симметричной трехфазной системы равна нулю:

е_А + е_В + е_С = 0;

Е_А + Е_В + Е_С = Е_Ф (1 + а² + а) = 0.

Полученное равенство справедливо при соединении фаз (обмоток) генератора звездой (фазы имеют общий узел) и треугольником (фазы соединены последовательно). Наиболее часто фазы генератора соединяют звездой, а общий узел, называемый нейтралью, заземляют. Провод, соединяющий нейтральную точку генератора (точка N) и нейтраль нагрузки (точка n) при соединении звездой, называют нулевым проводом.

Различают симметричный и несимметричный режимы работы трехфазной цепи. При симметричном режиме сопротивления всех трех фаз одинаковы и ЭДС образуют симметричную систему, в противном случае имеет место несимметричный режим.

На практике применяются различные комбинации соединений, например: 1) генератор может быть соединен звездой, а нагрузка - звездой или треугольником; 2) генератор может быть соединен треугольником, а нагрузка - звездой или треугольником. Рассмотрим подробно две комбинации, когда обмотки генератора соединены звездой, а нагрузка - звездой и треугольником.

Соединение звезда – звезда с нулевым проводом (рис. 4.2)

N

Расчет трехфазной цепи, так же как и всякой сложной цепи, ведется обычно в комплексной форме. Если ЭДС фазы А равна Е_А, то ЭДС фаз В и С равны соответственно

Е_В = а²Е_А; Е_С = аЕ_А.

Концы фазных обмоток генератора и приемника называются нейтральными точками (N, n), а соединяющий их провод нулевым.

Линейные провода – это провода, соединяющие обмотки генератора с приемником. Напряжение между линейными проводами (U_AB, U_BC, U_CA) и токи в них (I_A, I_B, I_C) называют линейными.

Напряжения на фазах (сопротивлениях) нагрузки (U_A, U_B, U_C) и токи в них называют фазными. При соединении фаз звездой фазные токи равны линейным: I_Л = I_ф.