11.Кластерный анализ
Кластерный анализ — задача разбиения заданной выборки объектов на подмножества, называемые кластерами, так, чтобы каждый кластер состоял из схожих объектов, а объекты разных кластеров существенно отличались. Задача кластеризации относится к статистической обработке, а также к широкому классу задач обучения без учителя. Кластерный анализ — это многомерная статистическая процедура, выполняющая сбор данных, содержащих информацию о выборке объектов, и затем упорядочивающая объекты в сравнительно однородные группы (кластеры). Кластер — группа элементов, характеризуемых общим свойством, главная цель кластерного анализа — нахождение групп схожих объектов в выборке.
Задача и условия
Кластерный анализ выполняет следующие основные задачи:
Разработка типологии или классификации.
Исследование полезных концептуальных схем группирования объектов.
Порождение гипотез на основе исследования данных.
Проверка гипотез или исследования для определения, действительно ли типы (группы), выделенные тем или иным способом, присутствуют в имеющихся данных.
Независимо от предмета изучения применение кластерного анализа предполагает следующие этапы: — Отбор выборки для кластеризации. — Определение множества переменных, по которым будут оцениваться объекты в выборке. — Вычисление значений той или иной меры сходства между объектами. — Применение метода кластерного анализа для создания групп сходных объектов. — Проверка достоверности результатов кластерного решения.
Кластерный анализ предъявляет следующие требования к данным: во-первых, показатели не должны коррелировать между собой; во-вторых, показатели должны быть безразмерными; в-третьих, их распределение должно быть близко к нормальному; в-четвёртых, показатели должны отвечать требованию «устойчивости», под которой понимается отсутствие влияния на их значения случайных факторов; в-пятых, выборка должна быть однородна, не содержать «выбросов». Если кластерному анализу предшествует факторный анализ, то выборка не нуждается в «ремонте» — изложенные требования выполняются автоматически самой процедурой факторного моделирования (есть ещё одно достоинство — z-стандартизация без негативных последствий для выборки; если её проводить непосредственно для кластерного анализа, она может повлечь за собой уменьшение чёткости разделения групп). В противном случае выборку нужно корректировать.
11.1. Кластерный анализ в программной среде statistica
Одним из непреложных
условий корректного проведения
статистических исследований является
требование обеспечения однородности
признаков объектов. В качестве признаков,
характеризующих объект, будем использовать
совокупность всех переменных, т. е.
изменяемых факторов
;
и
.
Обозначим общее количество признаков
.
Методика кластерного анализа состоит из следующих этапов:
1. Стандартизация исходных статистических данных.
2. Вычисление расстояний между признаками объектов и суммарное расстояние между объектами по всем признакам и составление матрицы расстояний между объектами.
3. Поиск наименьшего расстояния между объектами и объединение двух объектов с наименьшим расстоянием между ними в кластере.
4. Вычисление расстояний между объектами и формирующимися кластерами и преобразование матрицы расстояний между ними. Переход к пункту 3 и выполнение пунктов 3 и 4 до тех пор, пока не будут сгруппированы все объекты и кластеры в один общий кластер, после чего переход к пункту 5.
5. Выдача перечней объектов по выделенным кластерам и соответствующей дендрограммы с указанием расстояний между сформированными кластерами.
Расстояние от формирующегося кластера с вошедшими в него объектами до других объектов может вычисляться по следующим правилам.
Принцип ближайшего соседа.
,
при
;
(3.1.1)
,при
.
Принцип наиболее удаленного соседа.
,
при
;
(3.1.2)
,при .
3.Принцип среднего расстояния.
.
(3.1.3)
Принцип медианы.
.
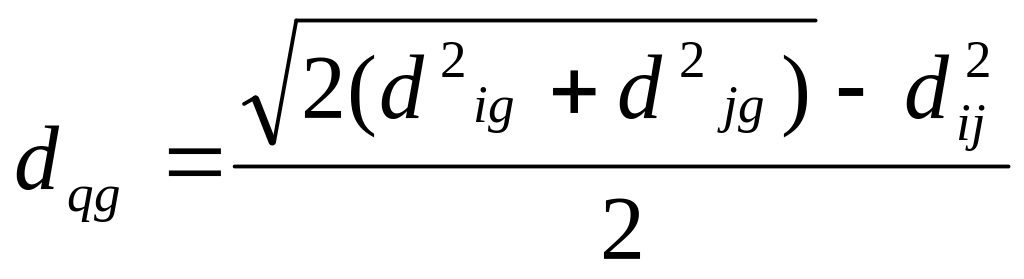(3.1.4)
В формулах (3.1.1)-(3.1.4) приняты следующие обозначения:
- расстояние между
q-ым
кластером, к которому подсоединен еще
один объект, и g-ым
объектом или кластером;
- расстояние между
i-ым
и g-ым
объектами или кластерами;
-
расстояние между j-ым
и g-ым
объектами или кластерами;
-
расстояние между i-ым
и j-ым
объектами или кластерами.
Первый этап для кластерного анализа проведем для «Кластерные усреднения & евклидова расстояния». В итоге определим Средние значения для каждого кластера:
В первой таблице указаны Средние значения для каждого кластера:
Таблица 11
В следующей таблице указаны, евклидовы расстояния и квадраты евклидовых расстояний между кластерами:
Таблица 12
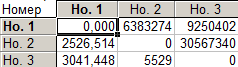
В данной таблице даны евклидовы расстояния между средними кластеров (по каждому из параметров внутри кластера вычисляется среднее, получается 3 точки в пятимерном пространстве, и между ними находится расстояние). Над диагональю в таблице даны квадраты расстояний между кластерами.
Далее определим дисперсионный анализ, где например, Между SS – внутригрупповая дисперсия (изменчивость), Внутренняя SS – межгрупповая дисперсия.
Таблица 13
Граф усреднений позволяет посмотреть средние значения для каждого кластера на линейном графике (графики средних значений характеристик районов для каждого кластера).
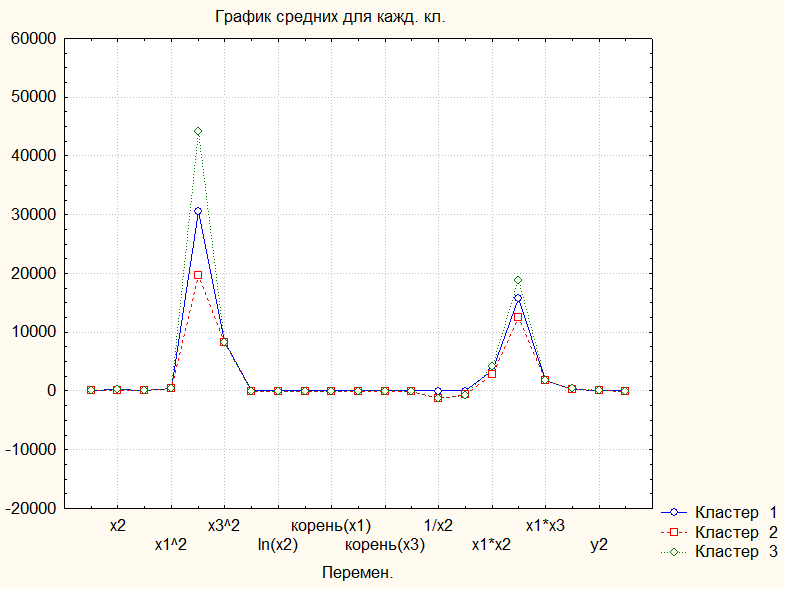
Рис.5 График средних для каждого кластера
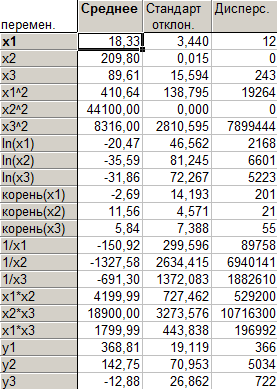
Описательная статистика для каждого кластера представляет электронные таблицы с описательными статистиками для каждого кластера (среднее, стандартное отклонение, дисперсия).
Описательная статистика для кластера 1
Таблица 14
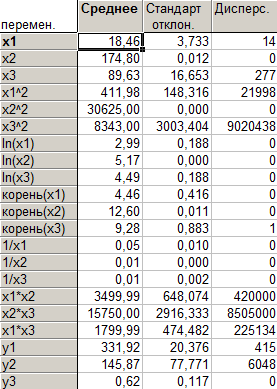
Описательная статистика для кластера 2:
Таблица 15
Описательная статистика для кластера 3:
Таблица 16
Элементы каждого кластера & расстояния
Элементы первого кластера и расстояния:
Таблица 17
Элементы второго кластера и расстояния:
Таблица 18
Элементы третьего кластера и расстояния:
Таблица 19
В итоге были произведены факторный и кластерный анализы, а так же оценка полученных результатов. Для факторного анализа были сравнены результаты двух типов вращений, а именно Варимакс исходных и Биквартимакс нормализованных, в результате существенных различий не обнаружилось. Хотя, теоретический считается, что для достижения простой структуры, в которой каждая переменная характеризуется преобладающим влиянием какого-то одного фактора, целесообразно применение метода вращения «Varymax», максимизирующего разброс квадратов факторных нагрузок по каждому фактору в отдельности и приводящий к увеличению больших нагрузок и уменьшению маленьких нагрузок.