7.Проверка «нормальности»

Нормальный закон является наиболее употребительным. Он применяется для представления самых различных случайных процессов, таких, как продолжительность жизни людей, изменения экономических и технических показателей.

Выскажем гипотезу, что исходные статистические данные подчинены нормальному закону, и в качестве параметров нормального закона примем оценки математического ожидания и среднего квадратического отклонения, вычисленные по формулам.

Функция плотности нормального закона имеет вид:

; .

Так как в нашем случае количество реализаций переменных сравнительно невелико, то для оценки предположения о нормальности принимаем критерий Колмогорова – Смирнова, используемый в пакете прикладных программ (ППП) Statistica 6.1.

;

; ,

где F*(v_ij) – эмпирическая функция распределения j-ой переменной для i-го значения;

F(v_ij) – гипотетическая функция распределения j-ой переменной для i-го значения;

d_j – абсолютная величина разности между эмпирической и гипотетической функциями распределения.

Значения гипотетической функции распределения находятся по статистическим таблицам [9].

; ; .

Если коэффициент доверия P_к предположению о нормальности эмпирического распределения, который можно найти по статистическим таблицам, не меньше 0,20, то предположение о нормальности не отвергается. Если Р_к <0,20, то предположение о нормальности рекомендуется отвергнуть.

Соответствие эмпирического и гипотетического распределений можно визуально проследить по графикам. При использовании критерия согласия Колмогорова предпочтительнее использовать функции распределения. Такие графики строятся и выдаются в специальных программных процедурах ППП Statistica 6.1 и Excel 2007 , на которые производится ориентация вычислений по излагаемому математическому аппарату.

Графики определения нормальности ИСД для распределений случайных величин представлены на рис.3.-8.

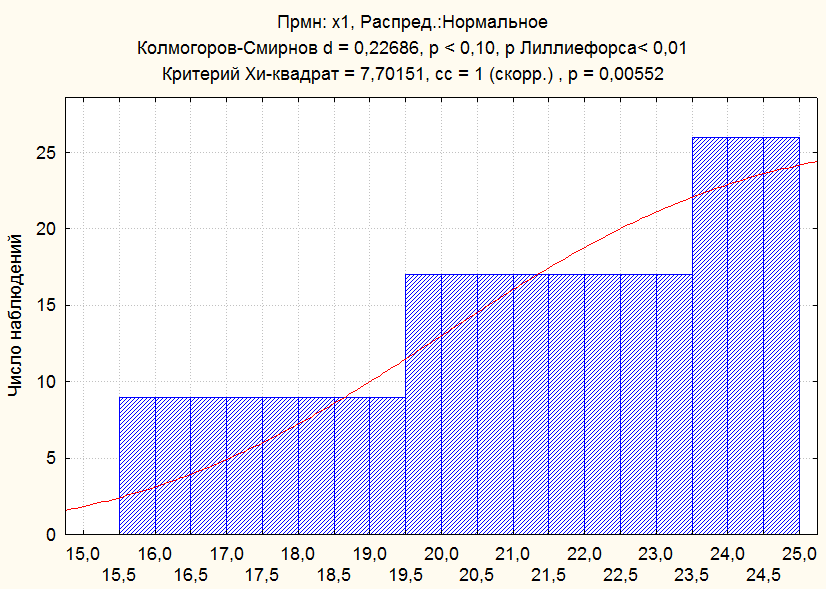
Рис.3. Эмпирическая и гипотетическая

функция распределения X1

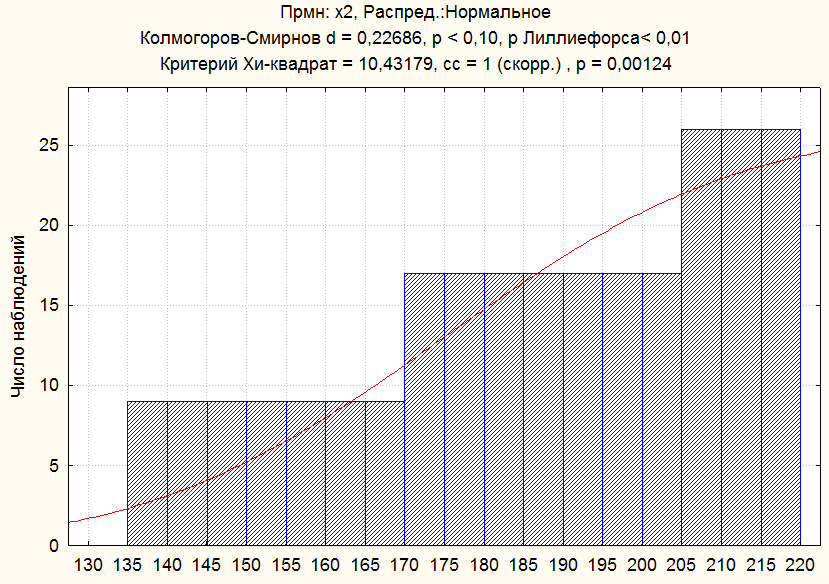
Рис.4. Эмпирическая и гипотетическая

функция распределения X2

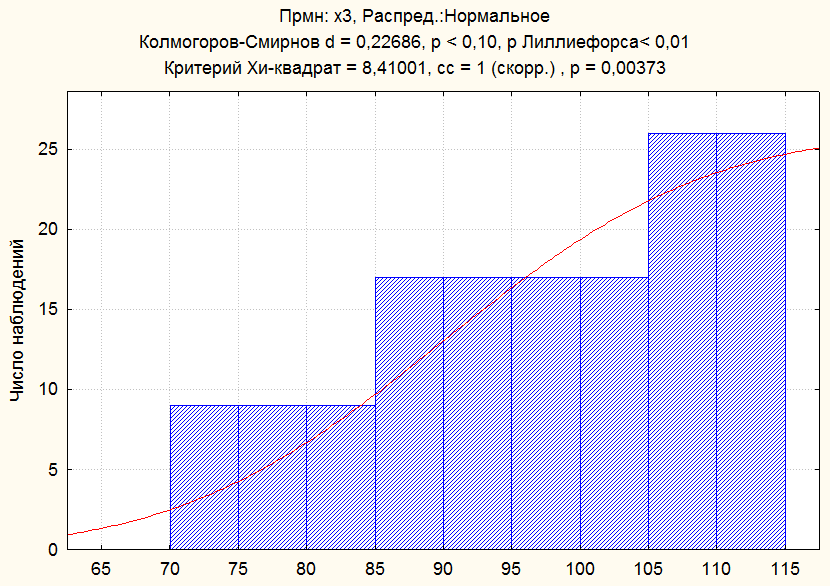
Рис.5. Эмпирическая и гипотетическая

функция распределения X3

Рис.6. Эмпирическая и гипотетическая

функция распределения У1

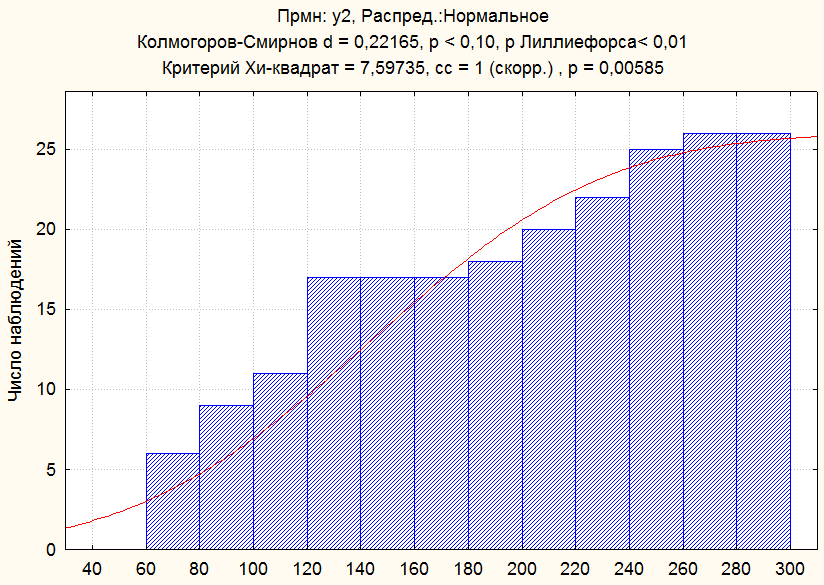
Рис.7. Эмпирическая и гипотетическая

функция распределения У2

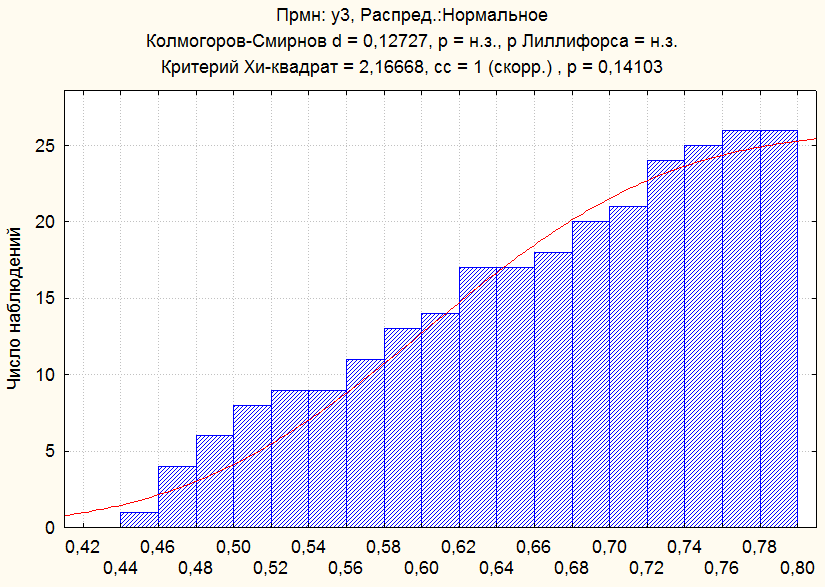
Рис.8. Эмпирическая и гипотетическая

функция распределения У3

Для анализа «нормальности» исходных статистических данных применен критерий согласия Колмогорова – Смирнова. Результаты представлены в таблице 6 Коэффициент доверия найден по статистическим таблицам.

Таблица 6

В 5 случае из 21, что составляет 24% ИСД соответствуют нормальному распределению по критерию Колмогорова-Смирнова. Из этого следует, что при увеличении количества учитываемых временных интервалов количество распределений, подчиненных нормальному закону, уменьшится.

8.Корреляционный анализ

Корреляция – это соотношение (взаимозависимость) случайных величин между собой. Тесноту связи между переменными принято характеризовать парными коэффициентами линейной корреляции, вычисляемыми по формуле:

;

; ,

где: n – количество учитываемых временных интервалов;

N – количество производственно-экономических факторов;

K – количество результативных показателей эффективности;

V – общее количество факторов внешней среды;

L – общее количество тарифных факторов;

- значение i-той (j-той) переменной на g-ом временном интервале.

Критическое значение коэффициента линейной корреляции:

; ; ,

где – критическое значение критерия Стьюдента для рекомендуемого уровня значимости , определяемого по статистическим таблицам при n–2 =27–2 = 25 степенях свободы.

n = 27– количество значений в ИСД.

Находим = .

Корреляционный анализ имеет как самостоятельное значение, так он может быть использован и для отбора факторов в уравнения регрессии (математическую модель). Целесообразно для этого найти значения коэффициентов линейной корреляции результативных показателей эффективности с факторами, с простыми функциями от факторов: х²; ln(x); √x; 1/х и с произведениями факторов между собой.

Исходные данные представлены в таблице 7:

Таблица 7

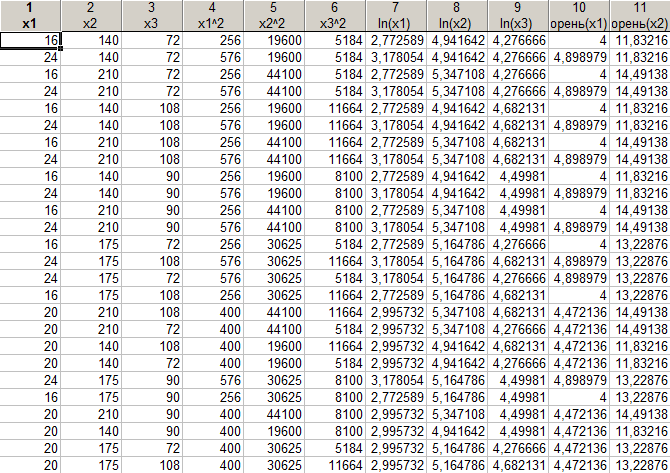
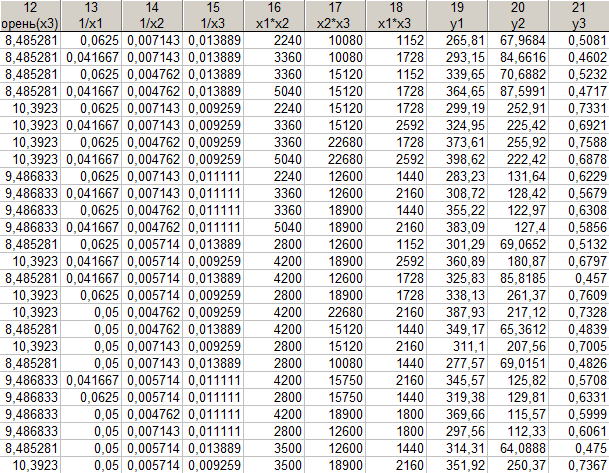
Рассмотрим корреляционную матрицу (см. таблицу 8).

Проанализируем силу связи показателей между собой по абсолютным значениям

Рассмотрим взаимосвязь факторов между собой. Положительная близкая к линейной связь имеется между следующими факторами:

х1	- х1^2, ln(x1), корень(х1), x1*x2, x1*x3;
х2	- х2^2, ln(x2), корень(х2), x1*x2, x2*x3;
х3	- х3^2, ln(x3), корень(х3), x1*x3, x2*x3;
х1^2	- ln(x1), корень(х1), x1*x2, x1*x3;
x2^2	- ln(x2), корень(х2), x1*x2, x2*x3;
x3^2	- ln(x3), корень(х3), x1*x3, x2*x3;
ln(x1)	- корень(х1), x1*x2, x1*x3;
ln(x2)	- корень(х2), x1*x2, x2*x3;
ln(x3)	- корень(х3), x1*x3, x2*x3;
корень(х1)	- x1*x2, x1*x3;
корень(х2)	- x1*x2, x2*x3;
корень(х3)	- x1*x3, x2*x3;
x1*x2	- x1*x3, x2*x3;
x2*x3	- x1*x3.

Отрицательная близкая к линейной связь имеется между следующими факторами:

х1	-1/x1;
х2	-1/x2;
х3	-1/x3;
х1^2	-1/x1;
x2^2	-1/x2;
x3^2	-1/x3;
ln(x1)	-1/x1;
ln(x2)	-1/x2;
ln(x3)	-1/x3;
корень(х1)	-1/x1;
корень(х2)	-1/x2;
корень(х3)	-1/x3;
1/x1	- x1*x2, x1*x3;
1/x2	- x1*x2, x2*x3;
1/x3	- x1*x3, x2*x3.

Рассмотрим взаимосвязь откликов между собой. Положительная близкая к линейной связь имеется между следующими результативными показателями:

у2

- y3.

Вычисленные значение и результаты анализа таблицы 8 позволяют сделать следующие обобщенные выводы:

Во-первых, коэффициенты линейной корреляции между факторами примерно в половине случаев по абсолютной величине превышают критическое значение. Поэтому уравнения регрессии могут содержать в себе факторы в первой и второй степени, а также в виде функций от факторов.

Во-вторых, величина корреляционной связи между факторами варьируется в весьма широких пределах. Абсолютная величина коэффициента линейной корреляции, меняющаяся в диапазоне от 0,00 до 1,00, показывает, что для сохранения всех переменных в уравнениях регрессии целесообразно использовать нелинейную регрессию

В-третьих, коэффициенты линейной корреляции между факторами в некоторых случаях превышают по абсолютной величине найденное критическое значение и достигают значения более 0,8. В таких случаях можно ожидать, что некоторые факторы могут не входить в уравнения регрессии и оказывать влияние на отклики через другие факторы с сильной корреляционной связью между ними.

Для коэффициентов линейной корреляции можно построить доверительные интервалы для принятой доверительной вероятности

; ; .