
- •3.38. Роль статистических методов в обеспечении и контроле качества. Схемы Исикава. Диаграммы Парето.
- •Причинно-следственная диаграмма или схема к.Исикава
- •Диаграмма Парето
- •3.39. Дисперсионный анализ и примеры его применения при управлении качеством
- •3.40. Регрессионный анализ и примеры его применения при управлении качеством
- •3.41. Корреляционный анализ и примеры его применения при управлении качеством
- •3.42. Общие понятия статистического приемочного контроля
- •Оперативная характеристика плана
- •3.43. Контрольные карты как метод статистического регулирования технологических процессов. Контрольные карты средних значений, дисперсий, размахов, коэффициентов вариации.
- •3.44. Оценка и статистический контроль показателя стабильности технологических процессов
- •4.45. Управление затратами на обеспечение качества. Функция потерь Тагути
3.40. Регрессионный анализ и примеры его применения при управлении качеством
В регрессионном анализе изучается связь между зависимой переменной Y и одной или несколькими независимыми переменными xj.
Рассмотрим парную регрессию, когда независимая переменная одна. Предположим, что переменная х (как правило, неслучайная величина) принимает некоторые фиксированные значения х1, х2,..., хn. Соответствующие значения зависимой переменной Y имеют разброс вследствие погрешности измерений и различных неучтенных факторов: у1, у2, ..., уn. Предположим, что связь между переменными линейная (рис. 5), тогда соответствующая регрессионная модель имеет вид:
Y=β0+β1x+ε
где β0 и β1 — параметры линейной регрессии;
ε — случайная ошибка наблюдений.

Рис. 5. Парная линейная регрессия
Предполагается, что ее математическое ожидание равно нулю, а дисперсия постоянна: М[ε] = 0, D[ε] =σ2.
Задача регрессионного анализа сводится к оценке параметров регрессии β0 и β1, проверке гипотезы о значимости модели и оценке ее адекватности: достаточно ли хорошо согласуется модель с результатами наблюдений?
Для оценки параметров
регрессии используется метод наименьших
квадратов: в качестве оценок принимаются
такие значения
![]() и
и
![]() ,
которые минимизируют сумму квадратов
отклонений εi
наблюдаемых
значений yi
от расчетных:
,
которые минимизируют сумму квадратов
отклонений εi
наблюдаемых
значений yi
от расчетных:
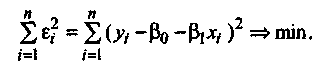
Приравнивая нулю производные по β0 и β1, получим зависимости для оценивания параметров модели:

![]()
где


Прогнозируемое по модели значение зависимой переменной
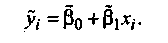
Разности между наблюдаемыми и прогнозируемыми значениями называются остатками, а соответствующая сумма квадратов — остаточной суммой квадратов:

Пусть

— общая сумма квадратов; сумма квадратов, обусловленная регрессией

Тогда остаточную сумму квадратов можно вычислить, используя основное тождество дисперсионного анализа

Парная линейная регрессионная модель называется незначимой, если параметр β1=0. Для проверки нулевой гипотезы H0: β1=0 используется статистика

которая при заданном уровне значимости α сравнивается с квантилью распределения Фишера F1-α (1, n-2) с числами степеней свободы 1 и (n-2).
Если оказывается F> F1-α (1, n-2), то нулевая гипотеза отклоняется: регрессионная модель статистически значима.
Кроме значимости, проверяется и адекватность модели. Приближенно адекватность можно проверить по диаграмме рассеяния с нанесенной на нее расчетной прямой (рис. 6).
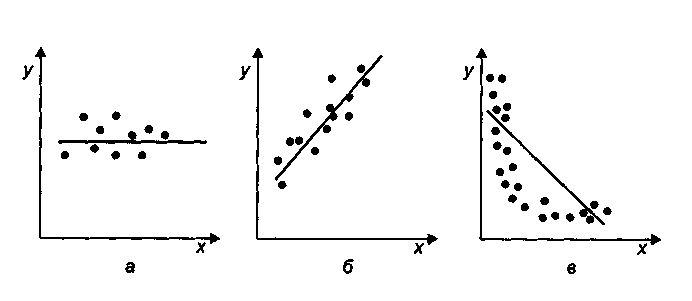
Рис. 6. Значимость и адекватность парной линейной регрессии:
а - модель незначима; б - модель значима и адекватна;
в - модель значима, но неадекватна
Пример
Исследуется зависимость между пределом прочности прессованной детали у (МПа) и температурой при прессовании х (град.). Предполагается наличие линейной зависимости между этими показателями. Экспериментально получены следующие данные (табл. 4):
Таблица 4
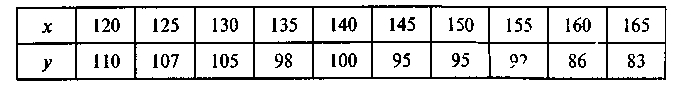
Объем выборки n=10. Выборочные средние:

Найдем оценки параметров линейной регрессии:


тогда
![]()
![]()
Уравнение линейной регрессии:
![]()
Диаграмма рассеяния и расчетная прямая показаны на рис. 7.

Рис. 7. Диаграмма рассеяния и парная линейная регрессия
Проверим значимость регрессии:
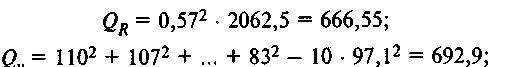
![]()
тогда
F=666,55 · (10-2) / 26,35=202,36.
Критическое значение статистики Фишера находим по статистической таблице:
F0,95 (1,8)=5,32.
Гипотеза о незначимости отклоняется, регрессионная модель значима.
