Тема 26. Геометричні нерівності та задачі на екстремум.

[7]: 9.3, 9.17, 9.24, 9.34, 9.43, 9. 52, 9.74, 11.5, 11.21, 11.33, 11.36

9.3. Дано n точок 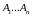і коло радіуса 1. Доведіть, що на колі можна вибрати точку М так, що .

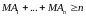9.17. Дано замкнену ламану, причому будь – яка інша замкнута ламана з тими ж вершинами має більшу довжину. Довести, що ця ламана не само перетинаюча.

9.24. Довести, що якщо довжини сторін трикутника пов’язані нерівністю 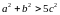, то с – довжина найменшої сторони.

9.34. В коло радіуса R вписаний многокутник площею S, який містить центр кола і на його сторонах вибрано по точці. Довести, що периметр випуклого многокутника з вершинами у вибраних точках не менше _.

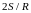9.43. Квадрат розрізаний на прямокутники. Довести, що сума площ кругів, описаних навколо всих цих прямокутників, не менше площі круга, описаного навколо вихідного квадрата.

9.52. Довести, що площа паралелограма, який лежить всередині трикутника не перевищує половини площі трикутника.

9.74. Довести, що якщо кути випуклого п’ятикутника утворюють арифметичну прогресію, то кожний з них більший за .

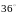11.5. Серед всих трикутників, вписаних в дане коло, знайти той у якого сума квадратів довжин сторін максимальна.

11.21. Дано трикутник АВС. Знайти всередині нього точку О для якої сума довжин відрізків ОА, ОВ, ОС мінімальна.(Зверніть увагу на випадок коли один з кутів трикутника більший за )

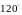11.33. На основі АD трапеції ABCD дано точку К. Знайти на основі ВС точку М для якої площа спільної частини трикутників AMD і BKC максимальна.

11.36. Серед всих многокутників, вписаних в дане коло, знайти той у якого сума квадратів довжин сторін максимальна.

Тема 27. Стереометричні задачі на обчислення.

[1]: 1999, 2004, 2022, 2062, 2111, 2150

1999. Основою прямого паралелепіпеда є ромб, гострий кут якого дорівнює а. Під яким кутом до основи треба провести січну площину, щоб в перерізі дістати квадрат, вершини якого лежать на бічних ребрах.

2004. Діагональ прямокутного паралелепіпеда утворює з більшою гранню кут α. Через менші сторони основ проведено січну площину. Знайти об’єм паралелепіпеда, якщо периметр перерізу дорівнює m, площина цього перерізу утворює з площиною кут β.

2022. В основі прямокутної призми лежить рівносторонній трикутник. Через одну з його сторін під кутом α до основи призми проведено площину, яка відтинає від призми трикутну піраміду, що має об’єм V. Знайти площу перерізу.

2062. Об’єм правильної трикутної піраміди дорівнює V, а двогранний кут при ребрі основи α. Знайти повну поверхню піраміди.

2111. Бічне ребро правильної зрізаної чотирикутної піраміди дорівнює l і утворює з площиною основи кут β. Діагональ піраміди перпендикулярна до бічного ребра. Знайти об’єм піраміди.

2150. Знайти довжину радіуса кулі, якщо при збільшенні його довжини на q см, об’єм сферичного сектора, який дорівнює V см³ , збільшується на p см³.

Тема 28. Застосування векторного та координатного методів до розв’язування задач стереометрії.

[27]: 17.024, 17.030, 17.043, 17.047, 17.056, 17.060, 17.088, 17.095

17.024. Скласти рівняння сфери, яка проходить через точку А(1; -1; 4) і дотикається до координатних площин.

17.030. Довести, що сума квадратів довжин всіх ребер паралелепіпеда рівна сума квадратів довжин всіх його діагоналей.

17.043. В правильній чотирикутній піраміді SABCD довжина кожного ребра рівна а. Точка і . Знайти кут між векторами і .

17.047. В прямокутному паралелепіпеді АВСDA₁ B₁ C₁ D₁ дано: АА₁=10, AD=6, AB=8. Знайти косинус кут між векторами і

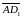
17.056. Знайти об’єм трикутної піраміди , побудованої на векторах і , якщо .

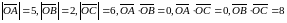17.060. Дано координати вершин піраміди: 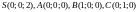. Знайти координати точки М, яка лежить на осі Oz s координат точки N, яка лежить в площині SBC, якщо відомо, що

17.088. Довести, що якщо сума квадратів протилежних ребер тетраедра рівні, то ці ребра попарно перпендикулярні.

17.095. Відомо довжини ребер тетраедра ABCD. Знайти косинус кута між протилежними ребрами AB і CD.