Тема 24. Застосування векторного та координатного методів до розв’язування задач планіметрії.

[27]: 17.043, 17.049, 17.063, 17.076, 17.116, 17.124

17.043. В правильній чотирикутній піраміді SABCD довжина кожного ребра рівна а. Точка 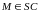і 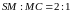. Знайти кут між векторами 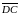і .

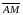17.049. Медіани бічних сторін рівнобедреного трикутника перетинаються під кутом . Знайти кут при вершині трикутника.

17.063. В трикутнику АВС точка N лежить на стороні АВ і AN=3NB; медіана АМ перетинається з CN в точці О. Знайти АВ, якщо АМ=СN=7 см і

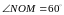
17.076. В трикутнику АВС дано: АВ=ВС; D – середина сторони АС; DK перпендикулярна ВС; точка М – середина відрізка DK. Довести, що прямі АК і ВМ перпендикулярні.

17.116. Навколо квадрата описано коло. Довести, що сума квадратів відстаней точок кола до вершин квадрата не залежить від вибору цих точок. Знайти цю суму.

17.124. В коло вписано трикутник АВС. Пряма, яка містить медіану СС₁ трикутника, перетинає коло вдруге в точці D. Довести, що

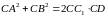
Тема 25. Планіметричні задачі на доведення.

[1]: 1616 – 1619,1718 – 1721, 1931, 1946, 1732 – 1735, 1767, 1769, 1787

1616. Довести, що трикутник, в якому медіана дорівнює половині сторони, на яку вона проведена, є прямокутником.

1617. Довести, що в прямокутному трикутнику медіана, проведена на гіпотенузу , дорівнює її половині.

1618. Довести, що в прямокутному трикутнику медіана і висота, проведені на гіпотенузу, утворюють кут, який дорівнює різниці гострих кутів трикутника.

1619. Довести, що квадрати катетів прямокутного трикутника відносяться як їх проекції на гіпотенузу.

1718. Довести, що для двох концентричних кіл сума квадратів відстаней довільної точки одного з них до кінців довільного діаметра другого є величина стала.

1719. Через одну з точок перетину двох кіл проведено діаметри кожного кола. Довести, що пряма, яка сполучає кінці цих діаметрів, проходить через другу точку перетину кіл.

1720. Довести, що коли через точку дотику двох кіл проведено дві січні і кінці їх сполучено хордами, то ці хорди паралельні.

1721. З точки Р до кола О проведено дві дотичні РА і РВ і через точку В проведено діаметр ВС. Довести, що прямі СА і ОР паралельні.

1732. Всередині рівностороннього трикутника взято довільну точку, з якої опущено перпендикуляри на сторони трикутника. Довести, що сума цих трьох перпендикулярів дорівнює висоті трикутника.

1733. Сторони трикутника дорівнюють 4 см, 13 см і 15 см. Всередині нього взято точку, віддалену на 5 см від першої сторони і на 1 см – від другої. Знайти відстань цієї точки від третьої сторони.

1734. У коло вписано правильний трикутник. Через середини двох дуг, що стягуються сторонами трикутника, проведено хорду. Довести, що сторони трикутника поділяють хорду на три рівні частини.

1735. На колі, описаному навколо рівностороннього трикутника АВС, взято довільну точку М. Довести, що найбільший з відрізків МА, ВМ, СМ дорівнює сумі двох інших.

1767. Довести, що медіани трикутника поділяють його на шість рівновеликих частин.

1769. Довести, що площа трикутника, сторони якого є медіанами другого трикутника, дорівнює 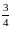площі цього трикутника.

1787. У паралелограмі середину кожної сторони сполучено з кінцем наступної сторони. Довести, що площа внутрішнього паралелограма дорівнює 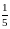площі заданого.

1931. Довести, що коли медіана і висота, проведені з однієї вершини кута трикутника, поділяють цей кут на три рівні частини, то такий трикутник прямокутний.

1946. Довести, що пряма, симетрична медіані відносно бісектриси внутрішнього кута трикутника, поділяє протилежну сторону на частини, пропорційні квадратам прилеглих сторін.