Тема 14. Комбінаторні сполуки та їх види. Біном Ньютона.
[6]: 1.880 – 1.883
Довести тотожності:
1.880.
,
де
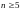
1.881.
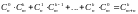
1.882.
Розв’язати рівняння:
[1]: 1534 – 1540, 1556 – 1558, 1581
Розв’язати рівняння:
1534.
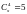
1535.
1536.
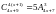
1537.
1538.
1539.
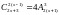
1540.
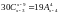
Довести, що:
1556.
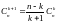
1557.
1558.
1581.
При якому значенні х
коефіцієнт четвертого члена розкладу
бінома
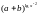дорівнює показнику бінома?
Тема 15. Доведення тригонометричних тотожностей і нерівностей.
[6]: 2.26 – 2.30, 2.38, 2.49, 2.58
Довести тотожності
2.26.
2.27.
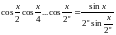
2.28.
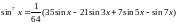
2.29.
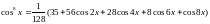
2.30.
Довести рівності:
2.38.
Довести умовні тотожності:
2.49.
, якщо
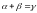
2.58. Довести нерівності:
а)
б)
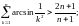
в)
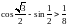
Тема 16. Розв’язування нестандартних тригонометричних рівнянь, нерівностей та їх систем. Тригонометричні рівняння з параметрами.
[6]: 2.114, 2.131, 2.156, 2.166 – 2.168, 2.176, 2.177
2.114. Розв’язати рівняння:
а)
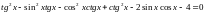
б)
в)
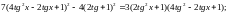
г)
д)
е)
є)
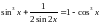
2.131.
2.156. Розв’язати нерівності:
а)
б)
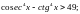
в)
г)
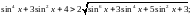
д)
е)
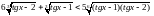
Розв’язати рівняння:
2.166.
2.167.
2.168.
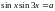
Розв’язати нерівності
2.176.
2.177.
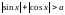
Тема 17. Доведення тотожностей і нерівностей, які містять обернені тригонометричні функції.
[6]: 2.266, 2.275, 2.276, 2.279, 2.282, 2.273
Довести, що:
2.266.
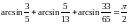
2.273.
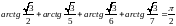
2.275.
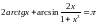, при
2.276.
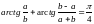
Довести нерівності:
2.279.
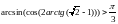
2.282.
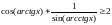
Тема 18. Розв’язування рівнянь і нерівностей, які містять обернені тригонометричні функції.
[6]: 2.308 – 2.310, 2.314, 2.327, 2. 328, 2.331 – 2.334
Розв’язати рівняння:
2.308.
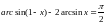
2.309.
2.310.
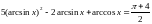
2.314.
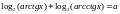
Розв’язати нерівності:
2.327.
2.328.
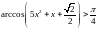
2.331.
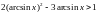
2.332.
2.333.
2.334.
Тема 19. Розв’язування нестандартних показникових рівнянь, нерівностей та їх систем. Показникові та логарифмічні рівняння з параметрами. Розв’язування показниково-степеневих рівнянь.
[2]: 9, 11, 17, 22, 31, 37, 60 (ст.164)
Розв’язати рівняння:
9.
11.
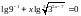
17.
22.
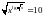
31.
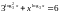
37.
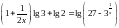
60.
7 (ст.171)
Розв’язати систему рівнянь:
7.
23, 24 (ст.177)
Розв’язати нерівності:
23.
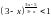
24.
27 (ст.180)
Розв’язати нерівності:
27.
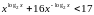
Тема 20. Контрольна робота
Тема 21. Основні властивості функцій. Застосування похідної у фізиці та геометрії. Застосування похідної до розв’язування рівнянь та нерівностей.
[20]: 56 (а), 57, 58, 67, 211, 224, 229, 230, 233 (а), 234 (а,б), 240 – 243
56.
а) Довести,
що для будь – якої функції
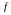з симетричною відносно точки О
областю
визначення функція
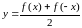парна, а функція
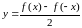непарна.
57.
Функція
і
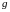періодичні
з загальним періодом
.
Довести, що функція
і
є періодичними з періодом
.
58. Довести, що сума двох неперервних періодичних функцій, визначених на всій числовій прямій і які не мають спільних періодів, не є періодичною.
67. При яких n функція може мати рівно n точок екстремуму, якщо відомо, що : а) парна; б) непарна; в) періодична функція?
211.
Довести,
що
функція
не має похідної в точці О.
224.
Довести,
що будь – яке кубічне рівняння
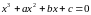має
хоча б один дійсний корінь.
229.
Три
пункти А, В, С не лежать на одній прямій,
причому
. Одночасно із точки А виїжджає автомобіль,
а із точки В – поїзд. Автомобіль рухається
в напрямку до В з швидкістю
,
поїзд – до С з швидкістю
.
В який момент часу (від початку руху)
відстань між поїздом і автомобілем буде
найменшою, якщо АВ=200 км?
230. На сторінці текст повинен займати 384 см2.Верхні і нижні поля повинні бути по 3 см, праве і ліве – по 2 см. Якщо взяти до уваги тільки економію паперу, то яким повинні бути найбільш вигідні розміри сторінки?
233.
Що більше:
а)
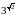або
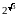
234.
Довести, що якщо
то:
а)
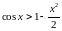
б)
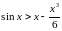
240.
Колесо
радіуса R
котиться по прямій. Кут φ повороту колеса
за t
секунд визначається рівнянням
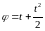. Знайти швидкість і прискорення руху
центра колеса.
241.
Лампа підвішена на висоті 12 м
над
прямою горизонтальною доріжкою по якій
іде людина зростом 1,8 м.
З якою швидкістю його тінь подовжується,
якщо він віддаляється від лампи зі
швидкістю
?
242.
Під
яким кутом перетинається графіки функцій
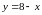і
?
243. Запишіть рівняння дотичної до графіка функції , яка проходить через точку М, якщо:
а)
б)
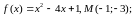
в)
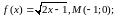
г)
