Тема 9. Доведення нерівностей.

[6]: 1.204 (а), 1.211, 1.223, 1.227

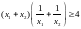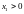1.204. (а) Довести нерівність ,де і

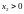
1.211. Довести нерівність 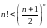при

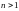
1.223. Довести, що для додатних a і b виконується нерівність

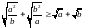
1.227. Довести нерівності

_а)

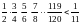
_б)

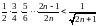
_в)

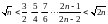
г)

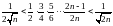
Тема 10. Функції “антьє” і “мантиси” в рівняннях і нерівностях.

[4]: 124, 125, 128, 129, 131, 134, 138, 143

Знайти множину цілих невід’ємних розв’язків і визначити кількість таких розв’язків:

124. (7-10)

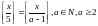
125. (8) Скільки існує натуральних чисел, третій степінь яких не перевищує 1 000 001 ?

128.(5-6)

129. (8-10) (Операції ділення на 2 і відшукання цілої частини повторені n раз)

131. (8-10)

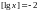
134. (8-10)

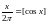
138. (8-10)

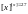
143. (8) Визначити х , якщо саме х, його ціла частина [x] і його дробова частина {x} утворюють геометричну прогресію.

Тема 11. Функціональні рівняння.

[5]: 1 (а – д), 2, 3 (ст.11), 1, 2 (ст. 7), 1 (ст.20)

1 (а – д), 2, 3 (ст.11),

1. Розв’язати функціональні рівняння:

_а)

_б)

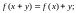
_в)

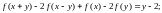
_г)

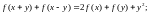
_д)

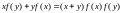
2. Знайти всі функції , які задовольняють функціональне рівняння 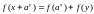, де а – деяка натуральна стала (параметр).

3. Знайти всі розв’язки функціонального рівняння де - дійсна функція, причому і для всіх виконується умова

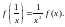
1, 2 (ст. 7)

1. Знайти неперервні функції , визначені на множині дійсних чисел, які задовольняють функціональні рівняння:

а)

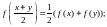
_б)

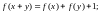
в)

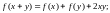
2. Знайти неперервні функції , визначені на множині додатних дійсних чисел, які задовольняють функціональні рівняння:

_а)

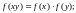
_б)

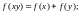
_в)

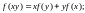
г) 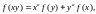де а – деяка дійсна стала (параметр).

1 (ст.20)

1. В класі диференційованих функцій розв’язати рівняння:

_а)

_б)

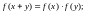
_в)

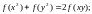
г)

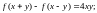
Тема. 12. Принцип Діріхле.

[3]: 1 – 8 (ст.54)

1. На ділянці лісу, яка має форму квадрата площею 1 км², на кожному прямолінійному відрізку довжиною 100 м росте принаймні одне дерево, радіус якого не менший 60 см. Чи можна стверджувати, що на ділянці не менше 7430 таких дерев?

2. Доведіть, що серед 82 кубиків, кожний з яких зафарбовано в певний колір, завжди можна вибрати 10 кубиків так, щоб вони всі були зафарбовані в різні кольори або в один колір.

3. Площину довільно розфарбовано у два кольори. Довести, що знайдуться дві точки одного кольору на відстані 1 м одна від одної.

4. Чи знайдеться число вигляду 111…100…0(починається з 1, а закінчується нулями), яке ділиться на 1992?

5. Доведіть,що серед будь – яких 1992 натуральних чисел можна вибрати кілька чисел таким чином, щоб їхня сума ділилась на 1992.

6. У клітинках шахової дошки 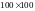записано цілі числа так, що різниця між будь – якими двома числами сусідніх клітинок(клітинки, які мають спільну сторону) не більша 20. Довести, що на дошці знайдеться принаймні три клітинки, в яких записано однакові числа.

7. Усередині квадрата, сторона якого дорівнює 1, розміщено 101 точку так, що жодні три не лежать на одній прямій. Довести, що серед цих точок знайдеться три таких, що площа трикутника, вершинами якого є ці точки, не перевищую 0,01.

8. У прямокутнику із сторонами довжиною 1 та 2 дано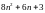 точок. Довести, що існує круг радіуса , який містить не менше трьох з даних точок.