Шкільний курс математики. Задачі підвищеної складності Завдання до практичних занять

МОДУЛЬ А

(рік навчання 5, семестр 2)

Тема 1. Раціональний дріб, його основні властивості. Умовні тотожності. Похідні пропорції.

[2]: 66 – 68

66. Розв’язати рівняння

67. Розв’язати рівняння

68. Розв’язати рівняння

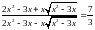
[4]: 249, 250, 253, 255, 256, 258, 260

249. (5-6) Скоротити дріб

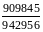
250. (5-6)Скоротити дріб

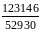
253. (6-10) Довести, що числа і 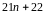взаємно прості для будь – якого натурального n.

255. ( 6-8) Знайти НСД двох чисел

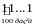і 1  111 111

256. (7- 8) Від прямокутника площею см² відрізають кілька квадратів см² доти, поки не залишиться прямокутник, довжина однієї із сторін якого менша за 62. Від отриманого прямокутника відрізають кілька квадратів із сторонами, довжина яких дорівнює меншій стороні прямокутника, і роблять так доти, поки не залишиться прямокутник, одна із сторін якого менша від сторони квадратів, що відрізаються. Так роблять, доки це можливо. Чому дорівнює сторона останнього відрізаного квадрата?

258. (8-10) m і n – два взаємно простих числа, і 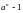обидва діляться на деяке число p . Довести, що тоді для будь – якого натурального k 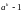ділиться на p.

260. Довести, що коли 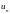і 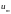- два числа Фібоначчі, то їхній НСД дорівнює 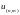, де (n,m) – найбільший спільний дільник n і m, тобто

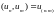
Тема 2. Теорема Безу та її застосування.

[2]: 1, 4, 8 –10, 13 – 16

1. Знайти остачу від ділення

4. При якому значенні а многочлен 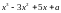при діленні на 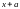дає остачу, яка дорівнює 4?

_8. При яких значеннях a і b многочлен 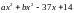ділиться на ?

9. Розкласти на множники

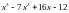
_10. Розкласти на множники

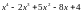
13. Розв’язати рівняння

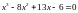
_14. Розв’язати рівняння

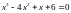
15. Розв’язати рівняння

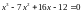
16. Розв’язати рівняння

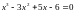
[1]: 23 – 28

Розкласти на множники:

23.

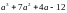
24.

25.

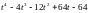
26.

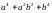
27.

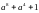
28.

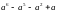
Тема 3. Прогресії та послідовності. Обчислення сум.

[4]: 210, 112, 215 – 218, 221, 222 – 225

210. (8-9) Довести, що арифметична прогресія складається з попарно взаємно простих чисел.

212. (6-9) Знайти арифметичну прогресію, що складається з трьох простих чисел p, p+10, p+20. Довести, що не існує арифметичної прогресії з різницею 10, що складається з взаємно простих чисел, причому має більше трьох чисел.

215. (8) Числа утворюють арифметичну прогресію. Довести, що

216. (8-9 )Числа x, y і z утворюють арифметичну прогресію. Довести, що коли x, y, z – цілі розв’язки рівняння то x кратне трьом, y – чотирьом, а z – п’яти.

217. (8-9) Числа x, y, z і u утворюють арифметичну прогресію і є цілими розв’язками рівняння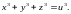 Довести, що x кратне трьом, y – чотирьом, z – п’яти, u - шести.

218. (8-10) Знайти корені рівняння 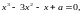якщо відомо, що вони утворюють арифметичну прогресію.

221. (8-10)Розв’язати систему рівнянь

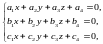
де 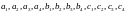утворюють арифметичну прогресію і відомо, що x, y, z, які є розв’язком цієї системи рівнянь, також утворюють арифметичну прогресію.

222. (8-9) Всі члени зростаючих арифметичної і геометричної прогресій додатні, перші і треті однакові, другі відрізняються на 2, а четверті на 14. Знайти ці прогресії.

223. (8-9) У арифметичної і геометричної прогресій перші члени дорівнюють одиниці, треті однакові, а сума четвертих дорівнює нулеві. Знайти ці прогресії .

224. (8-9) Навести приклади арифметичної і геометричної прогресій, у яких однакові перший і другий члени. Встановити залежність, що зв’язує ці дві прогресії.

225. (8-10) Що можна сказати про арифметичну і геометричну прогресії, у яких однакові перший, m-й і (2m-1)-й члени?