
- •1. Если функция непрерывна на отрезке, то она ограничена на нем.
- •2. Теорема Вейерштрасса:
- •3. Теорема Больцано-Коши:
- •3. Степенные ряды. Первая теорема Абеля. Параметры и радиус сходимости. Равномерная сходимость степенного ряда. Непрерывность суммы. Почленная дифференцируемость. Ряд Тейлора.
- •7. Законы больших чисел и предельные теоремы: неравенство Маркова, неравенство Чебышева, теорема Чебышева, центральная предельная теорема.
- •10. Многочлены. Кольцо многочленов над кольцом с единицей. Делимость многочленов, теорема о делении с остатком. Значение и корень многочлена. Теорема Безу.
- •12. Сравнения и вычеты. Кольцо вычетов. Малая терема Ферма. Сравнения первой степени. Китайская теорема об остатках.
- •15. Алгоритмы поиска в последовательно организованных файлах. Бинарный и интерполяционный поиск. Поиск в файлах, упорядоченных по вероятности. Самоорганизующиеся файлы. Оценки трудоемкости.
- •16. Основные понятия защиты информации (субъекты, объекты, доступ, граф.Доступов, информационные потоки). Постановка задачи построения защищённой автоматизированной системы (ас). Ценность информации.
- •18. Модель системы безопасности hru. Основные положения модели. Теорема об алгоритмической неразрешимости проблемы безопасности в произвольной системе.
- •Модель распространения прав доступа Take-Grant.
- •Теоремы о передаче прав в графе доступов, состоящем из субъектов, и произвольном графе доступов.
- •Расширенная модель Take-Grant и ее применение для анализа информационных потоков в ас.
- •20. Модель Белла-Лападулы как основа построения систем мандатного разграничения доступа. Основные положения модели. Базовая теорема безопасности (bst).
- •Модель Белла-Лападулы
- •Теорема bst (Basic Security Theorem).
- •21. Основные положения критериев tcsec (“Оранжевая книга”). Фундаментальные требования компьютерной безопасности. Требования классов защиты.
- •22. Основные положения рд гтк в области защиты информации. Определение и классификация нсд. Определение и классификация нарушителя. Классы защищенности ас от нсд к информации.
- •23. Общая характеристика операционных систем (ос). Назначение и возможности систем семейств unix, Windows.
- •24. Основные механизмы безопасности средств и методы аутентификации в ос, модели разграничения доступа, организация и использование средств аудита.
- •Методы аутентификации в ос.
- •Модели разграничения доступа
- •25. Субъекты в операционных системах (основные определения, содержимое дескрипторов процессов и потоков, переключение процессов и потоков).
- •26. Методы и средства обеспечения конфиденциальности информации в операционных системах семейства Windows nt и Linux.
- •27. Методы и средства обеспечения целостности информации в операционных системах семейства Windows nt и Linux.
- •28. Методы и средства обеспечения доступности информации в операционных системах семейства Windows nt и Linux.
- •29. Источники угроз и общие методы защиты от них в операционных системах Windows nt и Linux.
- •30. Компоненты системы защиты операционных систем семейства Windows nt и их характеристика.
- •31. Объекты в ос. Модель разграничения доступа в операционных системах семейства Windows nt.
- •32. Права, привилегии, суперпривилегии и вход пользователей в ос семейства Windows nt.
- •33. Компоненты системы защиты, модель разграничения доступа и способности в операционных системах семейства Linux.
- •34. Вредоносное программное обеспечение. Классификация, принципы работы, способы выявления и противодействия.
- •35. Соотнесение операционных систем семейства Windows nt и Linux с требованиями рд гтк. Место систем защиты информации в операционных системах.
- •36. Локальные вычислительные сети ieee 802.3. Методы и средства обеспечения безопасности в проводных сетях
- •37. Беспроводные локальные сети ieee 802.11. Методы и средства обеспечения безопасности в беспроводных сетях.
- •38. Виртуальные лвс. Типы vlan. Стандарт ieee 802.1q. Формат маркированного кадра Ethernet ieee 802.1p/q. Правила продвижения пакетов vlan 802.1q.
- •39. Межсетевые экраны. Классификация межсетевых экранов. Типовое размещение межсетевого экрана в лвс. Архитектура межсетевых экранов. Политика межсетевых экранов. Понятие dmz. Трансляция ip-адресов.
- •40. Системы обнаружения атак. Классификация систем обнаружения атак. Типовая архитектура систем обнаружения атак. Методы обнаружения информационных атак в системах обнаружения атак.
- •41. Языки запросов. Языки описания данных. Языки манипулирования данными. Особенности языковых средств управления и обеспечения безопасности данных в реляционных субд.
- •42. Транзакции. Свойства acid транзакций. Управление восстановлением. Алгоритм aries. Двухфазная фиксация.
- •43. Транзакции. Свойства acid транзакций. Управление параллельностью. Блокировки. Строгий протокол двухфазной блокировки.
- •44. Технологии удалённого доступа и системы бд, тиражирование и синхронизация в распределённых системах бд.
- •45. Классификация демаскирующих признаков и их характеристики
- •46. Технические каналы утечки информации, классификация и характеристика.
- •47. Оптические каналы утечки информации. Способы и средства противодействия наблюдению в оптическом диапазоне.
- •48. Канал утечки информации за счет пэмин
- •49. Каналы утечки акустической информации.
- •50. Материально-вещественные каналы утечки информации.
- •51. Специальные технические средства предназначенные для негласного получения информации (закладные устройства). Классификация, принципы работы, методы противодействия.
- •52. Задачи и принципы инженерно-технической защиты информации.
- •53. Способы и средства инженерной защиты и технической охраны объектов.
- •54. Методики оценки возможности утечки информации.
- •55. Методики оценки эффективности применяемых мер защиты информации.
- •56. Способы и средства информационного скрытия речевой информации от подслушивания. Энергетическое скрытие акустического сигнала.
- •57. Основные методы защиты информации техническими средствами.
- •58. Основные понятия криптографии. Модели шифров. Блочные и поточные шифры. Понятие криптосистемы. Ключевая система шифра. Основные требования к шифрам.
- •59. Системы шифрования с открытыми ключами: rsa, системы Эль-Гамаля, системы на основе «проблемы рюкзака».
- •60. Цифровая подпись. Общие положения. Цифровые подписи на основе шифросистемы с открытыми ключами стандартов гост р и dss.
- •61. Функции хэширования. Требования предъявляемые к функциям хэширования. Ключевые функции хэширования. Безключевые функции хэширования.
- •62. Проблемы и перспективы развития криптографических методов защиты. Криптосистемы на основе эллиптических кривых. Алгоритм электронной подписи на основе эллиптических кривых EcPsa.
- •63. Объекты правового регулирования при создании и эксплуатации системы информационной безопасности.
- •64.Использование существующих нормативных актов для создания системы информационной безопасности. Основные положения руководящих правовых документов.
- •65.Система международных и российских правовых стандартов. Стандарт bs7799.
- •66. Требования Доктрины информационной безопасности рф и ее реализация в существующих системах информационной безопасности.
- •67.Значение и отличительные признаки методик служебного расследования фактов нарушения информационной безопасности от расследования других правонарушений.
- •69. Понятие и основные организационные мероприятия по обеспечению информационной безопасности.
- •70.Политика информационной безопасности как основа организационных мероприятий. Основные требования к разработке организационных мероприятий
- •71. Контроль и моделирование как основные формы организационных действий при проверке действенности системы информационной безопасности.
- •72. Разграничение прав доступа как основополагающее требование организационных мероприятий и их практическая реализация на объекте защиты.
- •73. Иерархия прав и обязанностей руководителей и исполнителей при построении системы информационной безопасности, их взаимодействие.
- •74. Аудит системы информационной безопасности на объекте как основание для подготовки организационных и правовых мероприятий. Его критерии, формы и методы.
- •75. Общая характеристика и этапы проведения работ по обеспечению информационной безопасности автоматизированной информационной системы
- •76. Анализ защищенности автоматизированной информационной системы
- •77. Методы оценки информационной безопасности ас
- •78. Пути повышения надежности и отказоустойчивости информационной системы.
- •79. Технология обнаружения воздействия нарушителя на работу автоматизированной информационной системы
- •80. Основные принципы формирования нормативно-методических документов по обеспечению безопасности информации организации.
- •81. Жизненный цикл автоматизированной информационной системы. Этапы жизненного цикла.
- •82. Классические модели жизненного цикла автоматизированной информационной системы. Современные концепции и модели жизненного цикла.
- •1. Классические модели жизненного цикла
- •1.2 Современные стратегии конструирования программного обеспечения
- •1.3 Быстрая разработка приложений (RapidApplicationDevelopment)
- •1.4 Быстрая разработка приложений
- •1.4 Компонентно-ориентированная модель.
- •1.5. Экстремальное программирование (xp – extremeprogramming)
- •83. Порядок создания автоматизированных систем в защищенном исполнении.
- •84. Типовое содержание работ по защите информации на стадиях создания автоматизированных систем в защищенном исполнении.
- •85. Разработка технического задания на создание автоматизированной системы в защищенном исполнении. Этапы и виды работ.
- •86. Структурный подход к разработке программного обеспечения автоматизированной системы. Общие понятия. Основные модели структурного подхода. Метод пошаговой детализации.
- •87. Объектно-ориентированный подход к разработке программного обеспечения автоматизированной системы. Общие понятия. Общая характеристика моделей. Общие понятия об языке uml.
- •88. Тестирование программного обеспечения. Модели тестирования белого и черного ящика. Виды испытания и их характеристика.
- •89. Разработка аппаратного обеспечения (рао) автоматизированной системы. Этапы разработки. Общая характеристика этапов.
- •Этапы разработки
- •90. Научно-исследовательская разработка для создания новых видов аппаратного обеспечения
- •91. Опытно-конструкторская разработка новых видов аппаратного обеспечения.
- •92. Подготовка производства изделия на предприятии–изготовителе.
- •93. Применение средств криптографической защиты информации при проектировании автоматизированных систем в защищенном исполнении.
- •94. Особенности построения систем электронной цифровой подписи.
- •95. Подходы к разработке систем электронных платежей. Принципы функционирования платежных систем.
- •96. Концепции хранилищ данных. Свойства хранилищ данных. Архитектуры сппр с использованием концепции хранилищ данных.
- •97. Организация хранилищ данных. Многомерная модель данных. Факты и измерения. Информационные потоки хранилищ данных. Etl-процесс.
59. Системы шифрования с открытыми ключами: rsa, системы Эль-Гамаля, системы на основе «проблемы рюкзака».
Концепция криптографии с открытым ключом заключается в том, что для зашифрования и расшифрования используются разные ключи, причем зная значение одного ключа нельзя получить значение другого.
RSA.
Общая схема алгоритма:
каждый пользователь генерирует пару ключей: один для зашифрования и один для расшифрования;
пользователи публикуют ключи зашифрования в открытом доступе, а второй ключ, соответствующий открытому, сохраняется в секрете;
посылая пользователю В сообщение, пользователь А зашифровывает его открытым ключам пользователя В;
пользователь В расшифровывает полученное сообщение с помощью своего секретного ключа.
Пользователь
выбирает простые числа
 и
и
 ,
вычисляет
,
вычисляет
 и выбирает число
и выбирает число
 ,
взаимно простое с
,
взаимно простое с
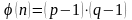 ,
где
,
где
 - функция Эйлера (равна количеству целых
чисел, меньших
и взаимно простых с
).
Далее находим число
- функция Эйлера (равна количеству целых
чисел, меньших
и взаимно простых с
).
Далее находим число
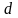 ,
обратное относительно умножения к
:
,
обратное относительно умножения к
:
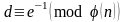 .
Ключ
.
Ключ
 является ключом шифрования, ключ
является ключом шифрования, ключ
 является ключом расшифрования. Шифрующее
преобразование:
является ключом расшифрования. Шифрующее
преобразование:
 ,
расшифровывающее преобразование:
,
расшифровывающее преобразование:
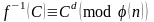 .
Легко заметить, что
.
Легко заметить, что
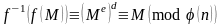
В
зависимости от поставленной задачи
(шифрование / ЭЦП), один из ключей
 ,
,
 засекречивается, а второй помещается
в общий доступ. Криптостойкость данной
системы основана на сложности разложения
числа
на простые множители
и
.
Для обеспечения лучшей криптостойкости
числа
и
должны различаться по размеру на
несколько десятичных разрядов, иметь
небольшой НОД (в идеале 1) и каждое из
них должно иметь хотя бы один большой
простой делитель.
засекречивается, а второй помещается
в общий доступ. Криптостойкость данной
системы основана на сложности разложения
числа
на простые множители
и
.
Для обеспечения лучшей криптостойкости
числа
и
должны различаться по размеру на
несколько десятичных разрядов, иметь
небольшой НОД (в идеале 1) и каждое из
них должно иметь хотя бы один большой
простой делитель.
ElGamal.
Безопасность
алгоритма основана на трудности
вычисления дискретных логарифмов в
конечном поле. Для генерации пары ключей
сначала выбирается простое число
и два случайных числа,
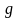 и
и
 :
:
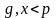 .
Затем вычисляется
.
Затем вычисляется
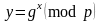 .
Открытым ключом являются
.
Открытым ключом являются
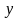 ,
и
.
И
и
можно
сделать общими для группы пользователей.
Закрытым ключом является
.
Для шифрования сообщения М
сначала выбирается
случайное число
,
и
.
И
и
можно
сделать общими для группы пользователей.
Закрытым ключом является
.
Для шифрования сообщения М
сначала выбирается
случайное число
 ,
взаимно простое с
,
взаимно простое с
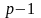 .
Затем вычисляются
.
Затем вычисляются
 и
и
 .
Пара
.
Пара
 является закрытым шифртекстом. Для
расшифрования
вычисляют:
является закрытым шифртекстом. Для
расшифрования
вычисляют:
 .
.
Система на основе «проблемы рюкзака».
Безопасность
алгоритмов рукзака опирается на NP-полную
проблему. Проблем рюкзака заключается
в следующем: пусть дан набор значений
M1,M2,…,Mn
и сумма S. Необходимо найти
значения biтакие,
что:
 ,
где
,
где
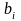 может быть либо нулем, либо единицей.
Существует 2 проблемы рюкзака. Проблема
рюкзака является «Легкой», если перечень
значений (Mi)
представляет собой сверхвозрастающую
последовательность (когда каждый член
больше суммы всех предыдущих). Решение
заключается в сравнении суммы (S)
с самым большим числом последовательности.
Если S больше, либо равен
этому числу (Mi),
то biпринимают
за «1». Уменьшаем S на
значение Mi
и переходим к следующему числу
последовательности. Процесс повторяется,
пока последовательность не закончится.
Если по окончании S равно
нулю, то решение найдено. Проблема
рюкзака является «Трудной», если перечень
значений (Mi)
– не сверхвозрастающая последовательность.
Алгоритма быстрого решения не найдено.
может быть либо нулем, либо единицей.
Существует 2 проблемы рюкзака. Проблема
рюкзака является «Легкой», если перечень
значений (Mi)
представляет собой сверхвозрастающую
последовательность (когда каждый член
больше суммы всех предыдущих). Решение
заключается в сравнении суммы (S)
с самым большим числом последовательности.
Если S больше, либо равен
этому числу (Mi),
то biпринимают
за «1». Уменьшаем S на
значение Mi
и переходим к следующему числу
последовательности. Процесс повторяется,
пока последовательность не закончится.
Если по окончании S равно
нулю, то решение найдено. Проблема
рюкзака является «Трудной», если перечень
значений (Mi)
– не сверхвозрастающая последовательность.
Алгоритма быстрого решения не найдено.
В основу алгоритма рюкзака Меркла-Хеллмана лежит идея шифровать сообщение, как решение набора проблем рюкзака. Сверхвозрастающая последовательность рюкзака является закрытым ключам, а нормальная – открытым.
Для
шифрования данных используется нормальная
последовательность, которая получается
из сверхвозрастающей следующим образом:
 Здесь
Здесь
 - член сверхвозрастающей последовательности,
- член сверхвозрастающей последовательности,
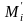 -
полученный член нормальной последовательности
для шифрования,
-
полученный член нормальной последовательности
для шифрования,
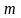 - число, большее суммы элементов
сверхвозрастающей последовательности,
k- число, взаимно простое с
.
- число, большее суммы элементов
сверхвозрастающей последовательности,
k- число, взаимно простое с
.
Для
шифрования данные разбиваются на
блоки по n бит. Считается
сумма
 ,
которая является шифрованным текстом.
Нормальная последовательность
,
которая является шифрованным текстом.
Нормальная последовательность
 является открытым ключом шифрования.
является открытым ключом шифрования.
Для
расшифрования необходимо знать числа
и
.
Шифрованный текст преобразуется:
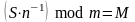 ,
где
,
где
 преобразуется алгоритмом расшифровки
сверхвозрастающего рюкзака в исходную
последовательность бит.
преобразуется алгоритмом расшифровки
сверхвозрастающего рюкзака в исходную
последовательность бит.
Реальные рюкзаки должны содержать не менее 250 элементов. Длина каждого члена сверхвозрастающей последовательности должна быть где-то между 200 и 400 битами, а длина модуля должна быть от 100 до 200 битов. В таком случае, полный перебор для взлома будет бессмысленным. На сегодняшний день существуют алгоритмы достаточно быстрого взлома оригинальной схемы и большинства её модификаций. Также есть варианты алгоритма рюкзака, считающиеся безопасными на сегодняшний день.
