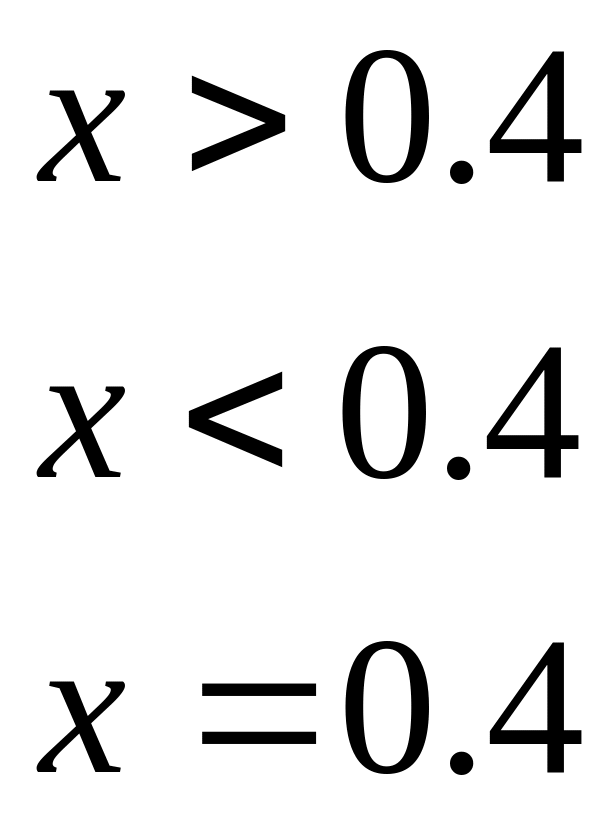Завдання 3 Для розгалуженої функції знайти значення функції для аргументу, визначеного користувачем.

№ п/п	Завдання
1	якщо
2	якщо
3	якщо
4	якщо
5	якщо
6	якщо
7	якщо
8	якщо
9	якщо
10	якщо

Завдання 4 Скласти алгоритм та програму розв’язку задачі:

1. Знайти значення функції y=(x+x²+1)·six x для х = {a, b} та визначити, яке з них більше. Значення a, b – ввести з клавіатури.

2. Для функції 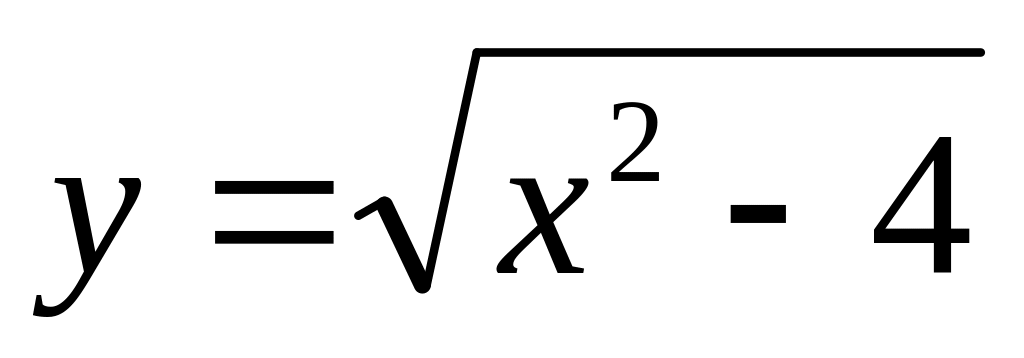знайти її значення для будь-якого значення аргументу х, визначеного користувачем з клавіатури. Якщо х – не входе в область визначення функції ( |x|≤2 ), то друкувати у відповідь повідомлення про це.

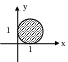3. М аємо довжину трьох відрізків - a, b, с (вводити з клавіатури). Визначити, чи можливо з них скласти трикутник. (кожна сторона менше суми двох других)

4. x,y – координати точки, визначені користувачем. Визначити, чи потрапила точка в область, приведену на малюнку. (якщо (х-1)²+(у-1)²=1 – точка на колі, (х-1)²+(у-1)²<1 – в колі, (х-1)²+(у-1)²>1 – за колом).

5. M, N – сторони прямокутного аркуша. Перевірити, чи можна з нього вирізати круг радіуса R. (min(M,N) ≥2R )

6. Відомі 2 менші кути трикутника – α, β (градуси). Визначити, чи трикутник прямокутний.

7. Відомі 2 значення аргументів функції - b, с (вводити з клавіатури). Визначити, чи спадае, зростає функція.

8. Відомі відомі значення функції на краях інтервалу YA, YB, і значення локального екстремуму YX. Визначити MIN I MAX функції.

9. За рівнянням параболи y=ax2+bx+c визначити, куди нахилені гілки, та координати вершини.

10. Відомі сторони трикутника a, b, с, введені за зростанням значень. Визначити, трикутник гострокутний, тупокутний, чи прямокутний.