7. Кинематика и динамика гексапода 6

Обратная задача кинематики для гексапода рассмотрена в п. 6.1. Поэтому сразу перейдем к рассмотрению прямой задачи.

7.1. Прямая задача кинематики. Примем обозначения и допущения, принятые в п. 6.2. Свяжем с основанием систему координат , а с платформой – систему координат (рис. 7.1).

Положение шарниров , в системе координат определяется, соответственно, векторами

, , . (7.1)

Положение платформы относительно основания задается углами Эйлера (рис. 6.5) и вектором .

Подобно тому, как это сделано в п. 6, геометрические соотношения между системами координат , определим с помощью ( )-матрицы однородных преобразований

.

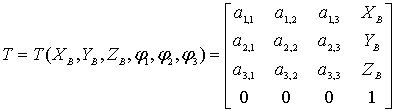Таким образом, положение шарнира , в системе координат задается вектором

. (7.2)

 

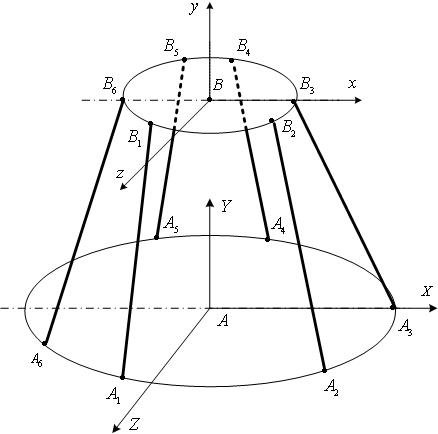
Рис. 7.1. Геометрия гексапода 6

 

Из формул (7.1), (7.2) следует, что обобщенную координату , как функцию величин , можно определить формулой

, . (7.3)

Выражения для линейных и угловых скоростей и ускорений концов штанг можно найти, дифференцируя и дважды дифференцируя по выражения (7.3). Однако эти выражения оказываются слишком громоздкими и мало пригодными для практического использования. Исследование скоростей и ускорений концов штанг проще производить с помощью имитационного моделирования (см. п. 8).

Заметим, что во введенных обозначениях углы между штангой , и осями системы координат определяются выражением

, ,

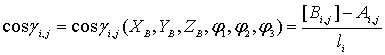где углы , , - углы между штангой и осями , , соответственно.

7.2. Динамика механизма. По методике, использованной в п. 6.3, найдем уравнения движения платформы в форме уравнений Лагранжа

, , (7.4)

где - кинетическая энергия системы; , , , , , - обобщенные координаты; - обобщенная сила, соответствующая -ой обобщенной координате.

Положим, что платформа, как твердое тело, симметрична относительно оси , так что ее моменты инерции равны: (рис. 7.1).

Массу платформы обозначим . В таком случае ее кинетическая энергия равна

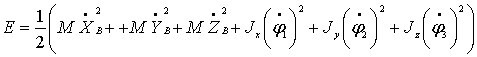. (7.5)

Выпишем силы, действующие на платформу, а также радиусы-векторы , , точек их приложения в проекциях на оси системы координат (рис. 6.6):

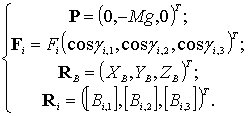(7.6)

Нам далее понадобятся матрицы Якоби векторов , . Аналогично тому, как это сделано в п. 6.3, из (7.6) имеем:

; ; ;

; ;

; ;

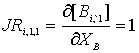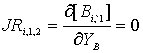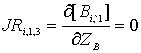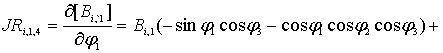
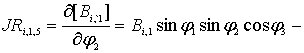
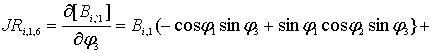
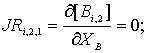
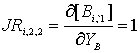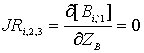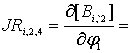
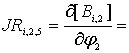
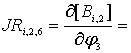
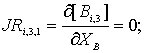
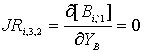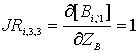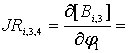
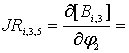
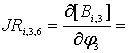
Составим выражение для работы на элементарных приращениях и, в соответствии с методикой составления уравнений Лагранжа, приравняем его нулю:

. (7.7)

Здесь

, , -

векторы элементарных приращений.

Поскольку , очевидно равенство . Таким образом, из выражений для компонентов матриц , следует, что элементы вектора определяются следующим образом:

 

 

Аналогично п. 6.3, в приведенных выше выражениях для , , обозначим коэффициент при , . В этих обозначениях получим более компактные выражения для элементарных приращений , , :

; (7.8)

; (7.9)

. (7.10)

Подставив выражения (7.8) – (7.10) в (7.7), после несложных преобразований получим выражение

+ .

Приравнивание в последнем выражении коэффициентов при независимых приращениях , дает следующие значения обобщенных сил:

; ; ;

; ;

Подставляя в уравнения (7.4) полученные выражения для обобщенных сил, а также выражения для кинетической энергии системы (7.5), получим искомую систему обыкновенных дифференциальных уравнений

, , , (7.11)

, (7.12)

, (7.13)

. (7.14)

В уравнениях (7.11) - (7.14) силы - это внешние (управляющие) силы, которые могут быть заданы как функции времени, как функции обобщенных координат , а также как функции длин «своих» штанг . Наоборот, при заданных законах изменения величин из этих уравнений могут быть найдены необходимые управляющие силы, как функции времени.