6. Кинематика и динамика гексапода 4

6.1. Обратная задача кинематики. Для гексапода (рис. 6.1) обратная кинематическая задача решается аналогично тому, как это сделано для трипода (п. 4).

Пусть обобщенными координатами являются длины штанг , ,…, соответственно. Пусть также в неподвижной декартовой системе координат координаты точек равны , а точек - , где , .

 

 

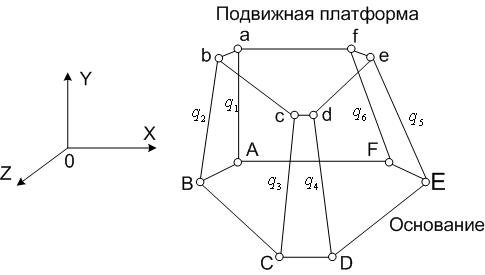
Рис. 6.1. Схема гексапода: - обобщенные координаты

 

Во введенных обозначениях решение обратной задачи кинематики для любого гексапода дает следующая система уравнений:

;

;

…

.

6.2. Прямая задача кинематики. Пусть , , - невесомые штанги, из числа которых штанги , состоят из двух полуштанг, связанных призматическими кинематическими парами. Штанги , присоединены к платформе в точках с помощью сферических шарниров, а к основанию в точках - с помощью карданных шарниров; штанга связана с основанием неподвижно, а с платформой – с помощью сферического шарнира (рис. 6.2).

 

 

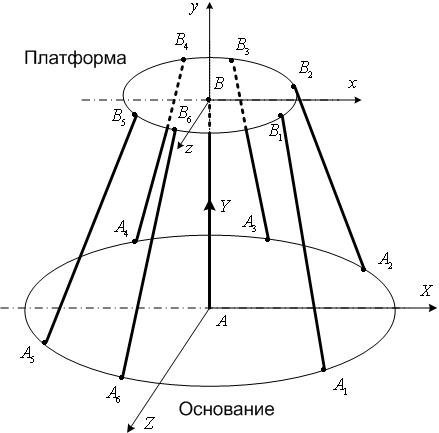
Рис. 6.2. Геометрия гексапода 4

 

Основание горизонтально и точки расположены на окружности радиуса с центром в точке A в вершинах квазирегулярного шестиугольника (рис. 6.3). Аналогично, точки  лежат на окружности радиуса с центром в точке B, в которой находится центр масс платформы (рис. 6.4). Штанги имеют длины , и наклонены к плоскости основания под углами , ( ). Расстояние между точкой и основанием (плоскостью ) обозначим  .

 

 

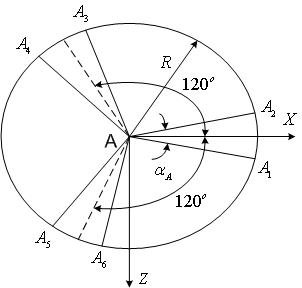
Рис. 6.3. Геометрия основания

 

 

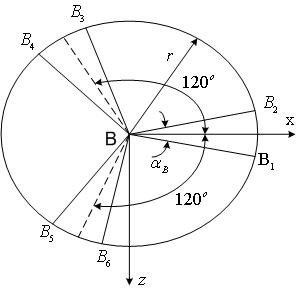
Рис. 6.4. Геометрия платформы

 

Заметим, что при проектировании параллельных механизмов рассматриваемого типа углы , следует выбирать из условия минимума или максимума некоторого критерия оптимальности, например, из условия максимума объема рабочей области манипулятора. В одной из работ рекомендуется использовать , [18].

Свяжем с основанием систему координат , а с платформой - систему координат так, как показано на рисунках 6.2 – 6.4.

Положение шарниров в системе координат определяется векторами

, . (6.1)

Если эти шарниры расположены так, как показано на рис. 6.3, то имеют место следующие выражения для компонентов этих векторов:

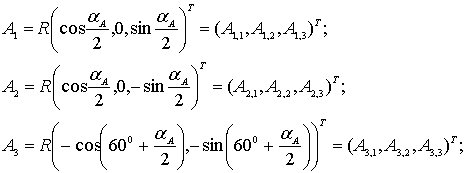
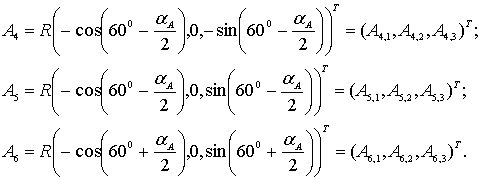
Аналогично, шарниры в системе координат имеют координаты

, (6.2)

и если эти шарниры расположены на платформе так, как показано на рис. 6.4, то имеем следующие выражения для этих координат:

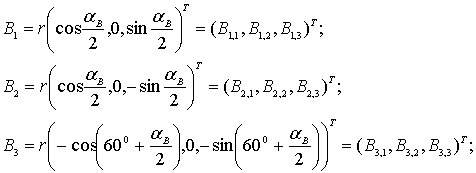
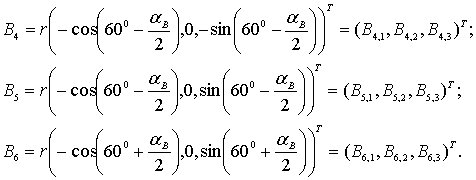
Положение платформы относительно основания зададим углами Эйлера (рис. 6.5) и вектором .

 

 

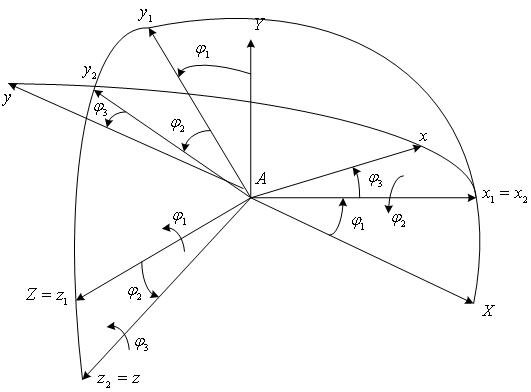
Рис. 6.5. К преобразованию систем координат

 

Таким образом, геометрические соотношения между системами координат , можно представить в виде ( ) матрицы однородных преобразований [12]

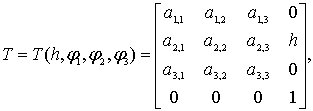(6.3)

где компоненты матрицы выражаются через углы Эйлера следующим образом:

Из выражений (6.2), (6.3) следует, что положение шарнира , в системе координат определяется вектором

.

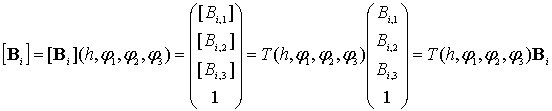(6.4)

Из формул (6.1), (6.2), (6.4) вытекает, что обобщенная координата , как функция расстояния и углов равна

, . (6.5)

Здесь любые две из величин , следует трактовать, как избыточные обобщенные координаты.

 

Выражения для скоростей и ускорений концов штанг (точек ) можно найти, дифференцируя и дважды дифференцируя по выражения (6.5). Однако эти выражения оказываются слишком громоздкими и мало пригодными для практического использования. Исследование скоростей и ускорений концов штанг проще производить с помощью имитационного моделирования (см. раздел 8).

6.3. Динамика механизма. По методике подраздела 5.2 найдем уравнения движения платформы в форме уравнений Лагранжа

, , (6.6)

где - кинетическая энергия системы; , , , - обобщенные координаты; - обобщенная сила, соответствующая -ой обобщенной координате.

Положим, что платформа, как твердое тело, симметрична относительно оси , так что ее моменты инерции равны: (рис. 6.2).

Массу платформы обозначим . В таком случае ее кинетическая энергия равна

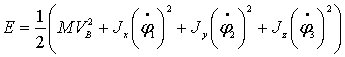, (6.7)

где - величина полной скорости центра масс платформы . Поскольку в системе координат вектор скорости , эта величина определяется выражением (рис. 6.2).

Выпишем силы, действующие на платформу, а также радиусы-векторы , , точек их приложения в проекциях на оси системы координат (рис. 6.6):

(6.8)

 

 

 

 

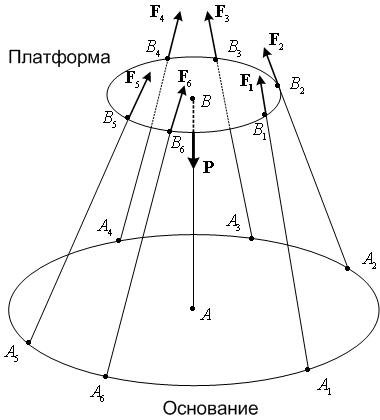
Рис. 6.6. Силы, действующие на платформу

 

Здесь

.

Нам далее понадобятся матрицы Якоби векторов , . Из выражений (6.4) следует, что компоненты матрицы определяются следующими формулами:

;

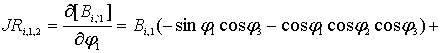
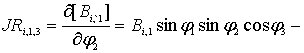
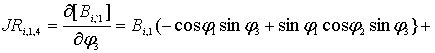
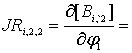
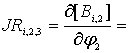
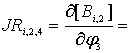
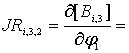
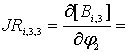
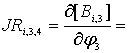
Составим выражение для работы сил на элементарных приращениях и, в соответствии с методикой составления уравнений Лагранжа, приравняем его нулю:

. (6.9)

Здесь

, , -

элементарные приращения соответствующих векторов.

Из выражений для компонентов матриц , следует, что элементы вектора определяются следующим образом:

 

 

В приведенных выражениях для , , обозначим коэффициент при элементарном приращении , :

…

Во введенных обозначениях имеем

, , , (6.10)

(6.11)

Подставив выражения (6.10), (6.11) в выражение (6.9), после несложных преобразований получим уравнение

+

+ .

Приравнивание в последнем выражении коэффициенты при элементарных приращениях дает следующие значения обобщенных сил:

;

;

;

Подставляя в уравнения (6.6) полученные выражения для обобщенных сил, а также выражение для кинетической энергии системы (6.7), получим искомую систему обыкновенных дифференциальных уравнений

, (6.12)

, (6.13)

, (6.14)

. (6.15)

В уравнениях (6.12) - (6.15) силы представляют собой внешние (управляющие) силы, которые могут быть заданы как функции времени, как функции обобщенных координат , а также как функции длин «своих» штанг . Наоборот, при заданных законах изменения величин из этих уравнений могут быть найдены необходимые управляющие силы, как функции времени.