5. Кинематика и динамика трипода 3

Обратная задача кинематики для данного трипода рассмотрена в п. 4.

5.1. Прямая задача кинематики. Пусть, как и в п. 4, невесомые штанги , состоят из двух полуштанг, связанных кинематическими парами типа P, присоединены к платформе в точках с помощью шарниров типа S, а к основанию в точках - с помощью U-шарниров; невесомая штанга , состоящая аналогично из двух полуштанг, связана с основанием неподвижно, а с платформой – с помощью U- шарнира (рис. 4.2).

Точки платформы образуют правильный треугольник со стороной и с центром в точке B, в которой находится центр масс платформы. Точки неподвижного горизонтального основания также образуют правильный треугольник со стороной a и с центром в точке A. Штанги имеют длины , и наклонены к плоскости основания под углами , ( ). Расстояние между точкой и основанием (плоскостью ) обозначим . Положим, как и ранее, , .

Свяжем с основанием систему координат таким образом, что начало координат A совпадает с центром симметрии основания, ось проходит через шарнир , ось направлена по нормали к основанию, а ось образует с осями , правую тройку. Аналогично, свяжем с платформой систему координат (рис. 4.2).

Положение шарниров в системе координат определяется векторами (4.14), а положение шарниров в системе координат - векторами (4.15).

Положение платформы относительно основания задается углами Эйлера (рис. 4.4) и вектором . Поэтому геометрические соотношения между системами координат , можно представить в виде ( ) матрицы однородных преобразований , аналогичной матрице (4.16).

Таким образом, положение шарнира , в системе координат можно задать вектором

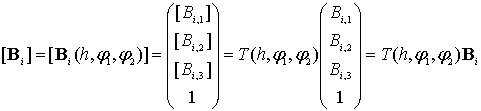. (5.1)

Итого, обобщенная координата , как функция расстояния и углов , определяется выражением, аналогичным выражению (4.17):

, . (5.2)

Выражения для скоростей и ускорений концов штанг легко найти, дифференцируя и дважды дифференцируя по выражения (5.2). Однако, в силу громоздкости получающихся выражений, исследование скоростей и ускорений концов штанг проще производить с помощью имитационного моделирования (см. п. 8).

5.2. Динамика механизма. По методике п. 4.5 найдем уравнения движения платформы в форме уравнений Лагранжа

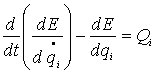, ,3, (5.3)

где - кинетическая энергия системы; , , - обобщенные координаты; - обобщенная сила, соответствующая -ой обобщенной координате.

Положим, что платформа, как твердое тело, симметрична относительно оси , так что ее моменты инерции равны: (рис. 4.2). Массу платформы обозначим . В таком случае ее кинетическая энергия равна

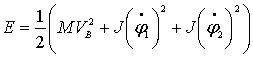, (5.4)

где - величина полной скорости центра масс B платформы. Поскольку в системе координат вектор скорости , эта величина равна, очевидно, (рис. 4.2).

Выпишем силы, действующие на платформу, а также радиусы-векторы , , точек их приложения в проекциях на оси системы координат (рис. 4.5):

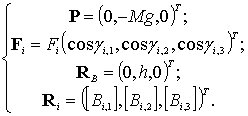(5.5)

Здесь, аналогично п. 4.5,

.

Нам далее понадобятся матрицы Якоби векторов , . Из выражения (5.1) для вектора следует, что компоненты матрицы определяются формулами

, , ;

, , ;

, ,

.

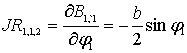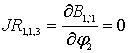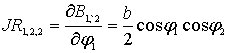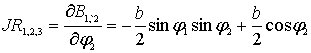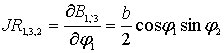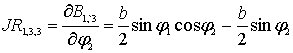Аналогично, из выражения (5.1) для вектора следуют выражения для компонентов матрицы :

, , ;

, ,

;

, ,

.

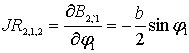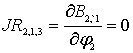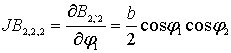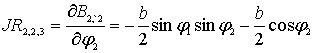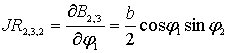По такой же схеме из выражений (5.1) для вектора вытекают выражения для компонентов матрицы :

, , ;

, , ;

, , .

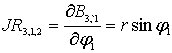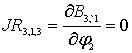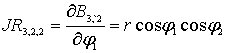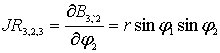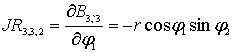Составим выражение для работы сил на элементарных приращениях и, в соответствии с методикой составления уравнений Лагранжа, приравняем его нулю:

. (5.6)

Здесь величины

,

,

представляют собой векторы элементарных приращений.

Из выражений для компонентов матриц , следует, что

,

,

.

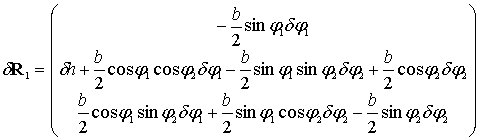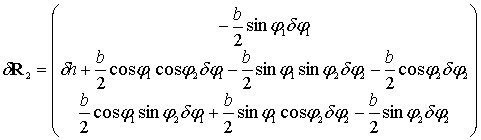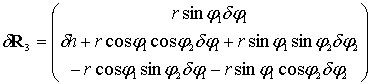Таким образом, учитывая (5.5), из (5.6) имеем

+

+

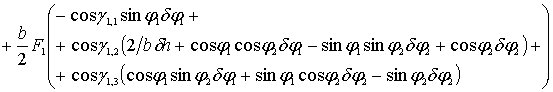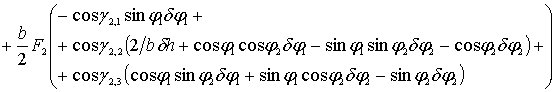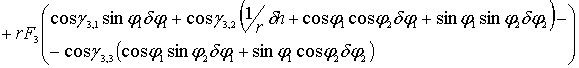=0. (5.7)

Приравнивая в выражении (5.7) коэффициенты при независимых приращениях , получим следующие значения обобщенных сил:

; (5.8)

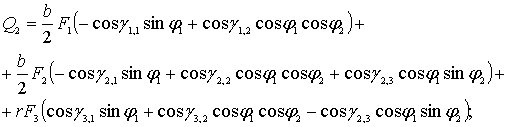
(5.9)

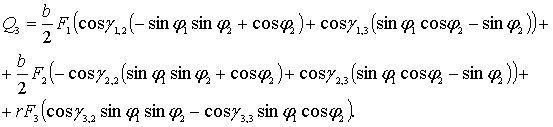
(5.10)

Подставляя выражения (5.8) – (5.10) в формулы (5.3), (5.4), получим искомую систему обыкновенных дифференциальных уравнений:

(5.11)

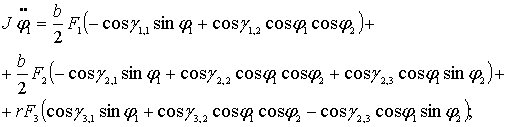
(5.12)

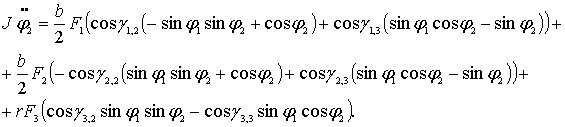
(5.13)

В уравнениях (5.11) – (5.13) силы - это внешние (управляющие) силы, которые могут быть заданы как функции времени, как функции обобщенных координат , а также как функции длин «своих» штанг . Наоборот, при заданных законах изменения величин из этих уравнений могут быть найдены необходимые управляющие силы, как функции времени.