4. Кинематика и динамика трипода 2

4.1. Обратная задача кинематики. Использование механизмов параллельной кинематики приводит к усложнению задач управления манипуляторами на основе этих механизмов. Однако некоторые задачи кинематики, например, обратная кинематическая задача, и для таких механизмов решаются просто.

Пусть обобщенными координатами являются длины штанг механизма , , соответственно (рис. 4.1). Пусть также в неподвижной декартовой системе координат координаты точек равны , а точек - , где , .

 

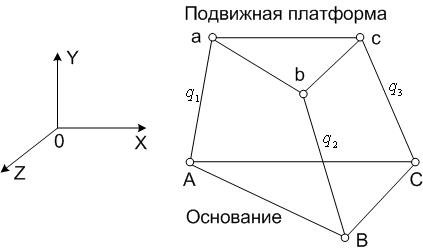
Рис. 4.1. Схема трипода: - обобщенные координаты

 

Легко видеть, что во введенных обозначениях решение обратной задачи кинематики для любого трипода дает следующая система уравнений:

;

;

.

4.2. Кинематика плоскопараллельного движения. Пусть невесомые стержни , , состоящие из двух полуштанг, связанных поступательными кинематическими парами, присоединены к платформе в точках с помощью сферических шарниров, а к основанию в точках с помощью карданных шарниров. Пусть также штанга присоединена к платформе в точке с помощью карданного шарнира, а к основанию в точке - неподвижно (рис. 4.2).

 

 

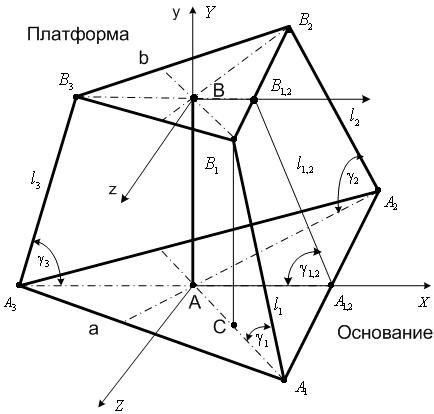
Рис. 4.2. Геометрия трипода 2

 

Точки образуют правильный треугольник со стороной и с центром в точке B, в которой находится центр масс платформы. Будем считать, что неподвижное основание горизонтально и точки также образуют правильный треугольник со стороной a и с центром в точке A. Штанги имеют длины , и наклонены к плоскости основания под углами , ( ). Опорная штанга имеет длину , и перпендикулярна основанию.

Далее нам понадобятся также следующие обозначения: , - середины отрезков , соответственно; - длина отрезка ; - угол между прямой и плоскостью основания (рис. 4.2).

Введём систему координат с центром в точке A, ось которой направлена по вектору , ось - вертикально вверх (от основания к платформе), а ось дополняет систему до правой тройки (рис. 4.2).

Вслед за работой [14] рассмотрим плоскопараллельные движения платформы, когда длины двух штанг (пусть это будут штанги ) и углы их наклона к основанию равны:

; . (4.1)

Если перемещение платформы производится с соблюдением условия (4.1), то, очевидно, точка перемещается в вертикальной плоскости . Платформа при этом имеет всего одну степень свободы (вращательную) и ее положение полностью определяется переменной - углом наклона платформы к основанию (рис. 4.3).

Определим переменную , как функцию обобщенных координат , . Из простых геометрических соотношений имеем

,

,

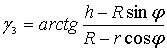, (4.2)

где , .

 

 

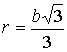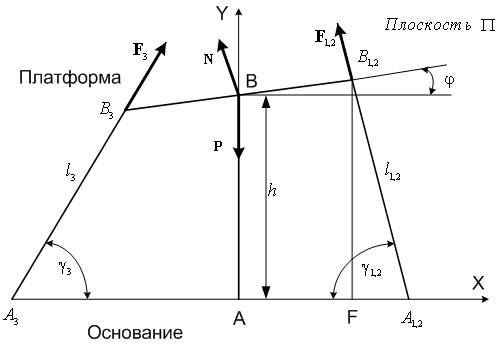
Рис. 4.3. Схема трипода 2 в плоскости симметрии

 

Из выражения (4.2) легко получить искомую функцию

. (4.3)

Аналогично для имеем (рис. 4.3)

,

,

,

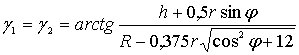. (4.4)

Таким образом, для искомая функция аналогична функции (4.3) и имеет вид

. (4.5)

Итак, поведение платформы в плоскопараллельном движении описывается всего одной обобщенной координатой или ; величины , определяемые формулой (4.5), следует трактовать, как избыточные обобщенные координаты.

Скорости и ускорения концов штанг (точек ) легко найти, дифференцируя и дважды дифференцируя по выражения (4.3), (4.5) соответственно. Так, например,

.

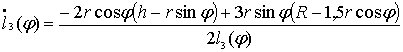4.3. Динамика плоскопараллельного движения. Уравнение движения платформы будет искать в форме уравнения Лагранжа

 

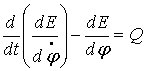, (4.6)

где - кинетическая энергия системы, - обобщенная сила.

Поскольку поступательные движения платформы отсутствуют, ее кинетическая энергия равна

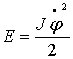, (4.7)

где - момент инерции платформы относительно оси, параллельной оси и проходящей через точку .

Выпишем силы, действующие на платформу, а также радиус-векторы точек их приложения в проекциях на оси системы координат :

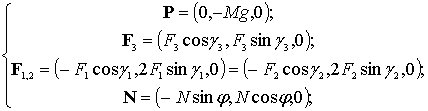(4.8)

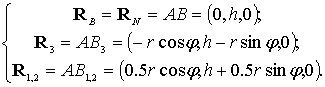(4.9)

Здесь - масса платформы, - ускорение свободного падения.

Из уравнений (4.8), (4.9) вытекает, что обобщенная сила определяется выражением

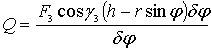
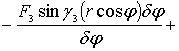
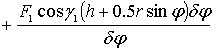
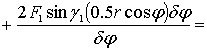
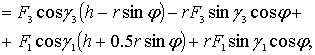(4.10)

где углы выражаются через обобщенную координату с помощью формул (4.2), (4.4).

Подставляя выражения (4.7), (4.10) в уравнение (4.6), получим искомое обыкновенное дифференциальное уравнение второго порядка

(4.11)

где углы , , как функции угла , определяются формулами

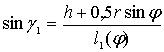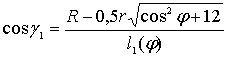, . (4.12)

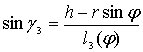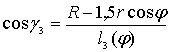, . (4.13)

Заметим, что в уравнении (4.11) силы , - это внешние (управляющие) силы, которые могут быть заданы как функции времени, как функции обобщенной координаты , а также как функции длин «своих» штанг , . Наоборот, при заданном законе изменения из (4.11) могут быть найдены необходимые управляющие силы, как функции времени.

Из уравнения (4.11) легко получить взаимосвязь между стационарными значениями сил , , т.е. значениями которые обеспечивают равновесие платформы при заданной обобщенной координате  . Действительно, если , то из (4.11) имеем уравнение

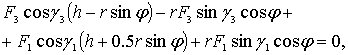
из которого следует, что

.

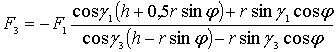Здесь , , , определяются выражениями (4.12), (4.13) соответственно.

4.4. Кинематика произвольного движения. Используем системы координат , (рис. 4.2). При этом положение шарниров в системе координат определяется векторами

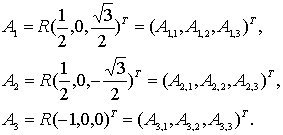(4.14)

Аналогично, положение шарниров в системе координат задается векторами

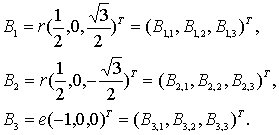(4.15)

Положение платформы относительно основания зададим углами Эйлера (рис. 4.4).

Тогда геометрические соотношения между системами координат , можно представить в виде ( ) матрицы однородных преобразований [12]

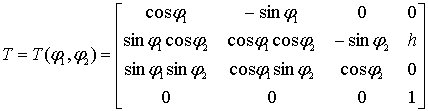. (4.16)

 

 

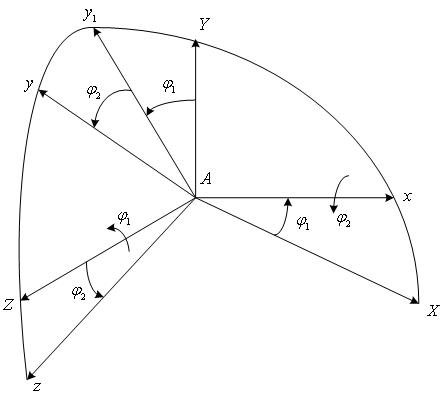
Рис. 4.4. К преобразованию систем координат

 

Таким образом, положение шарнира в системе координат задается вектором

.

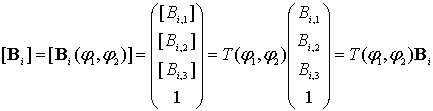Отсюда следует, что обобщенная координата , как функция углов определяется выражением

, (4.17)

где одну из величин следует трактовать, как избыточную обобщенную координату.

Выражения для скоростей концов штанг (точек ) легко найти из Якобина системы (4.17), т.е. дифференцируя по эту систему. Аналогично, ускорения концов штанг можно получить из матрицы вторых производных системы (4.17). Однако, как выражения для скоростей, так и выражения для ускорений оказываются слишком громоздкими и мало пригодными для практического использования. Исследование скоростей и ускорений концов штанг проще производить с помощью имитационного моделирования, например, с использованием программной системы MatLab [13] (см. п. 8).

4.5. Динамика произвольного движения. Примем обозначения и допущения, сделанные в п. 4.2. Расстояние между точкой и основанием (плоскостью ) обозначим . Введем также следующие обозначения: ; (рис. 4.2).

Поскольку поступательные движения платформы отсутствуют, уравнения движения платформы будем искать в форме уравнений Лагранжа

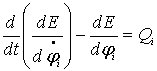, (4.18)

где - кинетическая энергия системы; - обобщенная сила, соответствующая -ой обобщенной координате.

Положим, что платформа, как твердое тело, симметрична относительно оси (рис. 4.2), так что ее моменты инерции равны: . В таком случае кинетическая энергия платформы определяется выражением

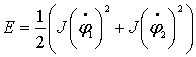. (4.19)

Положим, что поступательная кинематическая пара, связанная со штангой является пассивной. Выпишем силы, действующие на платформу, а также радиусы-векторы , точек их приложения в проекциях на оси системы координат (рис. 4.5):

;

;

.

Здесь - косинус угла между штангой и единичным вектором -ой оси системы координат ( соответствует ось , - ось , - ось ).

 

 

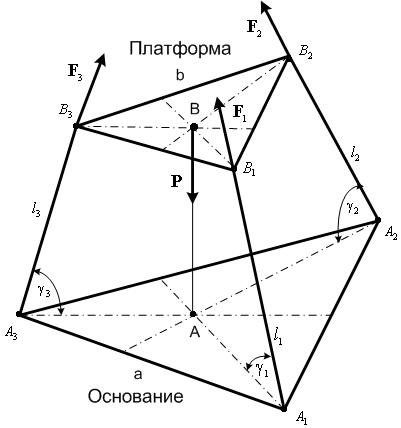
Рис. 4.5. Силы, действующие на платформу

 

Из определения скалярного произведения векторов легко получить явные выражения для косинуса угла , , :

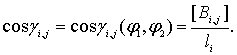
Таким образом, выражения для обобщенных сил имеют вид

=

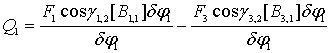(4.20)

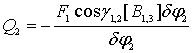= , (4.21)

где - элементарные приращения.

Подставляя выражения (4.19) - (4.21) в уравнение (4.18), получим искомую систему обыкновенных дифференциальных уравнений второго порядка

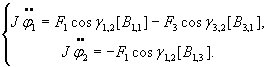(4.22)

Здесь силы , - это внешние силы, которые могут быть заданы как функции времени, как функции обобщенной координаты , а также как функции длин «своих» штанг , . Наоборот, при заданном законе изменения из уравнения (4.22) могут быть найдены необходимые управляющие силы, как функции времени.