Производственная функция Кобба–Дугласа:

a₀, a₁,a₂>0 – параметр нейтрального технического прогресса.

На микроуровне измеряется в различных единицах.

Свойства производственной функции:

1. Без ресурсов нет выпуска. y=f(0,0)=0;

2. Если какого-либо ресурса нет, то выпуск невозможен. y=f(0,y)=f(x,0)=0 выполняется не для всех производственных функций, например, если фактор заменяем)

3. Производственная функция монотонно возрастает по всем своим аргументам (свойство бесплатного распоряжения).

4. С ростом затрат одного вида ресурса при фиксированных затратах остальных ресурсов величина прироста выпуска на каждую дополнительную единицу ресурса не увеличивается. Иллюстрирует «закон убывающей эффективности производства» – показатель предельной эффективности по i- му ресурсу. Вторая частная производная показывает насколько убывает предельная эффективность производства.

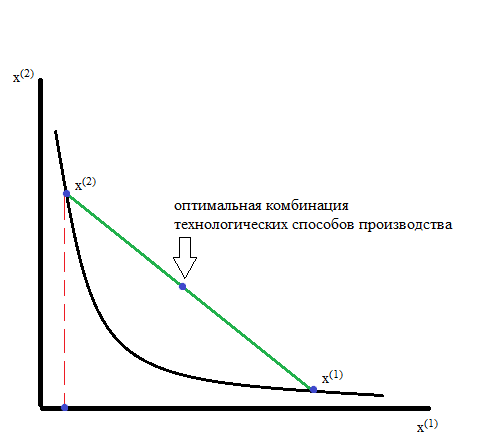
5. Свойства выпуклости. *² Интерпретация: если существует 2 способа производства одного и того же объема выпуска, то средневзвешенная комбинация этих способов производства позволит произвести, по крайней мере, столько же.

6. Свойство однородности производной функции. Производственная функция является однородной функцией степени p. p>0, описывает реакцию производства на изменение масштабов изменения затрат. a>0, a<1 – затраты снижаются, a>1 - затраты всех ресурсов возрастают. p- отражает эффект от изменения масштаба. p>1 – положительная отдача от масштаба, p<1 – отрицательный, p=1- постоянная отдача.

7. При неограниченном увеличении одного из факторов, выпуск неограниченно растет

Виды производственных функций.

1. Производственная функция Кобба-Дугласа. a₀ – параметр нейтрального технического прогресса a₁, a₂ – показатель эластичности по первому и второму виду ресурса a₁+a₂=1 классический вариант

2. Линейная производственная функция a₁, a₂ – удельные затраты ресурсов в расчете на единицу.

3. Производственная функция Леонтьева (производственная функция с постоянными пропорциями). a₁, a₂ > 0, определяют пропорцию, в которой факторы используются в производстве. a₁ единиц первого ресурса + a₂ единиц второго ресурса.

Если пропорции не выполняются, то один из ресурсов используются неэффективно.

Замещение ресурсов в данном случае невозможно.

4. Изокванты производственной функции. разные наборы ресурсов могут давать одинаковый выпуск. Линии, соединяющие такие наборы, называются изокванты изокванты являются линиями уровня производственной функции. Поэтому производственную функцию можно представить с помощью множества изоквант, связанных с различными уровнями выпуска продукции. Такое множество называется картой изоквант.

Примеры изоквант.

Для производственной функции Кобба-Дугласа		Для линейной функции

3. Для производственной функции Леонтьева

Свойства изоквант.

1. Изоквант – монотонно убывающие функции, выпуклые вниз;

2. Изокванты разного уровня не пересекаются, не касаются друг друга;

3. Чем выше и правее находится изокванта, тем большему уровню выпуска она соответствует.

Предельные и средние значения производственной функции.

Предельной производительностью или предельной эффективностью функции по i-му ресурсу называют первую частную производную производственной функции по этому ресурсу.

Предельная производительность показывает насколько единиц увеличится выпуск, если объем ресурсов увеличится на единицу, а затраты на остальные ресурсы останутся прежними.

Средняя производительность i-ого ресурса вычисляются как отношение выпуска к затратам этого ресурса.

Пример: для производственной функции Кобба-Дугласа.

При

Макроэкономические производственные функции Кобба-Дугласа, которые описывают ВВ в зависимости от затрат, характеризуются след.:

Y=f(K,L),

– капиталоотдача;

- средняя производительность труда;

– трудоемкость;

– капиталовооруженность труда.

– предельная капиталоотдача;

– предельная эффективность труда.