
- •Тема 1. Модели и моделирование в экономике
- •Понятие задачи и свойства модели
- •Этапы экономико-математического моделирования
- •Классификация моделей.
- •Экономико-математические дисциплины.
- •Тема 2. Моделирование поведения потребителей и спроса.
- •Пространство потребительских благ.
- •Потребительские предпочтения.
- •Функция полезности.
- •Виды функции полезности и кривых безразличия.
- •Свойства функций полезности.
- •Свойства кривых безразличия
- •Предельная норма замещения благ.
- •Монотонное преобразование функции полезности
- •Бюджетное множество
- •Модель потребительского выбора.
- •Геометрическая интерпретация решения задачи потребительского выбора.
- •Предельная полезность денег.
- •Свойства решения задач потребительского выбора.
- •15) Функция спроса
- •Кривая «доход – потребление»
- •Кривая «цена потребление».
- •16) Эффекты компенсации.
- •Г рафическое представление.
- •17)Уравнение Слуцкого.
- •18) Эластичность функции спроса.
- •Тема 3. Математические модели поведения производителей.
- •Понятие производственной функции
- •Показатели факторов производства – k, l
- •Производственная функция Кобба–Дугласа:
- •Свойства производственной функции:
- •Эластичность производства.
- •Определитель экономической эффективности и масштаба производства.
- •Предельная технологическая норма замещения.
- •Производственная функция с постоянной эластичностью замещения (ces- функция)
- •Тема: поведение фирмы в условиях совершенной конкуренции (ск)
- •Максимизация прибыли в краткосрочном периоде.
- •Минимизация издержек с заданным объемом выпуска.
18) Эластичность функции спроса.
Эластичность – это безразмерная величина, которая приближенно показывает насколько % изменяется значение показателя при изменении влияющего на него фактора на 1%.
Формула для вычисления эластичности в общем виде:
y=f(x)
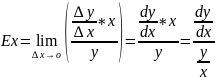
Коэффициент эластичности функции спроса по доходу оценивается % изменения спроса при 1% изменении дохода и фиксированных ценах.
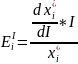
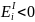 =>
малоценные товары
=>
малоценные товары
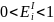 =>
товары низкой эластичности (осн. продукты
питания)
=>
товары низкой эластичности (осн. продукты
питания)
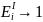 =>
товары со средней эластичностью
=>
товары со средней эластичностью
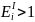 =>
товары с высокой эластичностью
=>
товары с высокой эластичностью
Коэффициент прямой эластичности спроса по цене показывает насколько % изменяется спрос на товар при увеличении цены на 1%, фиксированных ценах на остальные товары и фиксированных доходах.
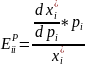
Если
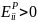 товар Гиффесса.
товар Гиффесса.
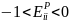 малоэластичный
товар
малоэластичный
товар
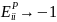 =>
среднеэластичный
=>
среднеэластичный
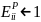 =>
высокоэластичный
=>
высокоэластичный
Коэффициент перекрестной эластичности по цене показывает насколько % изменяется цена товара при 1% изменении цены на другие товары при фиксированных остальных факторах.
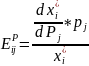
Если
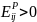 ,
то i-ый
товар заменяет j-ый.
,
то i-ый
товар заменяет j-ый.Если
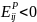 ,
то i-ый
товар дополняет j-ый
,
то i-ый
товар дополняет j-ый
Свойства коэффициента эластичности:
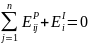
Пример:
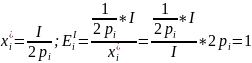 средняя
эластичность по доходу.
средняя
эластичность по доходу.
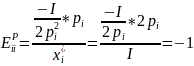 – средняя
эластичность по цене.
– средняя
эластичность по цене.
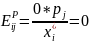 – нейтральны
– нейтральны
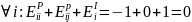
Тема 3. Математические модели поведения производителей.
Понятие производственной функции
В процессе производства фирма преобразует производственные ресурсы (факторы производства) в готовую продукцию, используют для этого определенные технологии производства.
В математической теории фирмы производство рассматривается как система «затраты – выпуск».

Связь, между затратами факторов и выпуском готовой продукции, заложена производственной функцией, которая каждому набору производственных факторов и существующей технологии ставят в соответствии определенный выпуск.
При этом полагается, что фирма работает эффективно, т.е. использует каждое сочетание факторов наилучшим образом. Это предположение о технологической эффективности производства.
Т.о., производственная функция описывает max выпуск продукции, кот. Фирма может осуществить при каждом определенном сочетании факторов и существующей технологии.
x=(x1,x2,…xn) – некоторый набор производственных ресурсов, вектор затрат.
xi – количество единиц i-ого вида ресурсов, затрачиваемых при производстве.
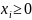
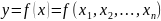
y- max объем выпуска при данных затратах n видов ре,сурсов для 1го товара- многофакторная производственная функция однопродуктовой фирмы.
Е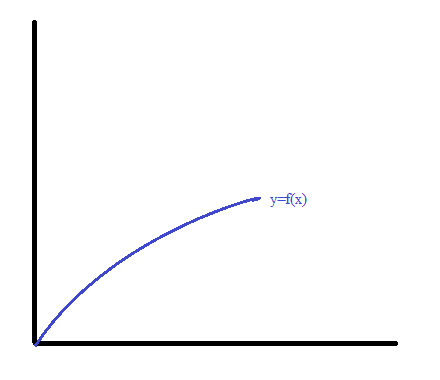 сли
в производстве используются только
один вид ресурса в количестве X,
то
производственная функция называется
однофакторной.
сли
в производстве используются только
один вид ресурса в количестве X,
то
производственная функция называется
однофакторной.
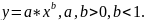
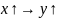
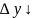 -
скорость роста постепенно уменьшается.
-
скорость роста постепенно уменьшается.
Иллюстрирует «закон уменьшающейся предельной эффективности производства»
y=f(x1,x2) – двухфакторная производственная функция .
Показатели факторов производства – k, l
На макроэкономическом уровне в качестве выпуска может рассматриваться ВВП.
Y=f(K,L), Y=f(K,L,N), N - природные ресурсы.
Y= НД, ВВП, ВП.
На макроуровне производственная функция – это статистическое устойчивая связь между затратами и выпуском.
