12. Предельная полезность денег.

Какой бы ни был вид функции полезности, множество Лагранжа дополнительная полезность пораждает ослабление бюджетного ограничения

Рассмотрим du(x*):

Получаем: , => - предельная полезность денег.

Множитель Лагранжа показывает дополнительную полезность, которую мы можем получить при увеличении бюджета на 1 рубль.

Свойства решения задач потребительского выбора.

1. Любое монотонное преобразование функции полезности не изменят решение задач потребительского выбора.

- решение.

Предположим, мы выполним монотонное преобразование:

– функция полезности, которая является монотонным преобразованием функции полезности.

=>

Подставим в I; получим

Вывод: решение не изменилось

2. При пропорциональном изменении всех цен и доходов потребителя, решение задач потребительского выбора не изменится.

Допустим, все P и I изменились в α раз. То с бюджетной линией произойдет следующее . Поэтому число α не влияет на решение задач потребительского выбора.

3. Решение задач потребительского выбора всегда находится на бюджетной линии.

4. Решение задач для различных функций полезности

   • 

Необходимо решить задачу:

Найдем производную от новой функции:

– оптимальное значение множителя Лагранжа

=> деньги, которые мы потратим на покупку 1 товара.

– доля дохода, которую мы тратим на потребление 1 товара

- второго товара

:

потребитель делит весь доход на 2 равные части.

• 

(угол наклона кривой безразличия)

1. 

2. (любой набор, на бюджетной линии)

Любая точка, лежащая на бюджетной линии

3. 

Частный случай:

a =b:

1. 

   Все деньги тратятся на более дешевый товар

2. 

3. 

• (абсолютно взаимодополняемые блага)

a единиц 1 блага потребляются с b единиц второго блага.

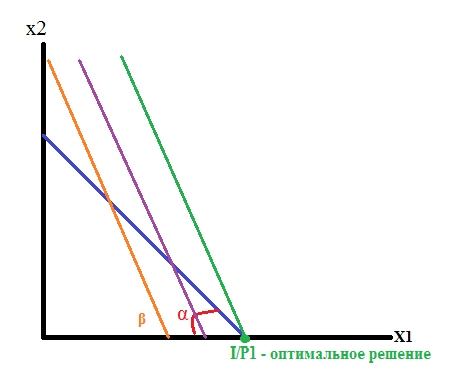
о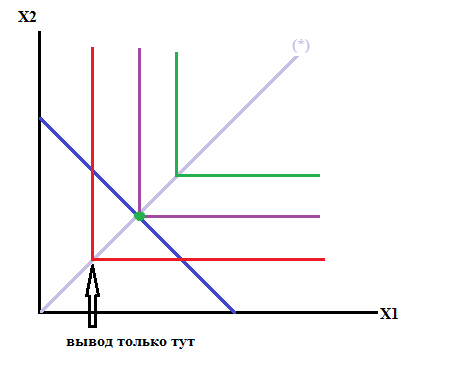 птимальное решение – пересечение луча с бюджетной линией

Частный случай

- один набор

15) Функция спроса

x^* - оптимальный набор

функция спроса

1. МП не меняет функцию спроса;

2. Пропорциональное изменение цен и дохода не меняет функцию спроса.

– однородная функция нулевой степени.

Кривая «доход – потребление»

Предположим, что цены не меняются, а меняется только доход

1. Если спрос возрастает при возрастающем доходе:

=> это ценные товары.

2. Если спрос падает, при возрастающем доходе

=> малоценные товары

К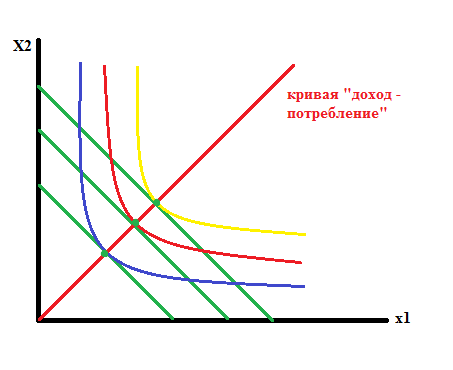 ривая «доход – потребление» показывает зависимость между спросом и доходом потребителя

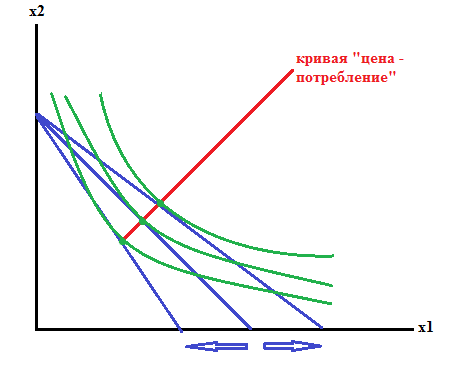
Кривая «цена потребление».

P_i возрастает

1. => обычные товары;

2. => товар Гиффена

В общем случае каждый товар можно отнести к одной из групп.

P\I	Ценные	Малоценные
Нормальные	Масло	Маргарин
Товары Гиффена	-----------------	Картофель в Ирландии в начале 19го века

Пример:

спрос на товары обычный

x₂(x₁)

- доход – потребление

=> прямая || оси ox (P₁ не зависит от x₂)

Найдем производные от

Они >0, при возрастающем доходе и возрастающем спросе.

при возрастающей цене и возрастающем спросе.