8. Монотонное преобразование функции полезности

Так как, важен лишь порядок потребительских наборов, то способ предписывания полезностей набора не может быть единственным. Если мы нашли один из способов, то это значит, что существует бесконечное множество способов описания тех же самых предпочтений.

Допустим, мы нашли функцию U(x), которая описывает предпочтения потребителя. Тогда любе монотонное преобразование будет являться функцией полезности, которая описывает те же самые предпочтении.

Монотонное преобразование – способ преобразования одного множества чисел в другое, при котором порядок чисел сохраняется (умножение на любое положительное число, прибавление любого числа, возведение в степень, логарифмирование).

U(x)) – ФП

Докажем это:

1. U(x) – ФП

2. – МП

- ФП

Пример:

Функция Кобба – Дугласа , a, b > 0

c, d > 0; c+d = 1

Преобразование приводит функцию к одинаковому виду.

Выбор потребителя одинаков в обоих случаях.

c, a, b >0

9. Бюджетное множество

X= (x₁,x2) – набор благ

P= (p₁,p₂) – цены на блага

P₁x₁+ P₂x₂ – стоимость товара

I – доход, бюджетное ограничение потребителя.

Бюджетным множеством называется множество наборов благ, расходы на потребление которых удовлетворяют бюджетному ограничению потребителя.

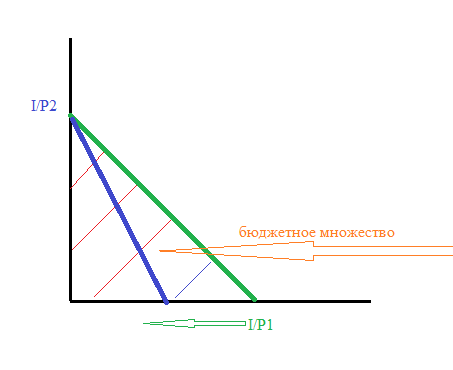– бюджетная линия

, ,

- количество 2го блага, при полном отказе от 1го

1. 

2. 

10. Модель потребительского выбора.

Мы будем рассматривать классическую модель, в основе которой лежат следующие гипотезы:

1. Доход потребителя ограничен;

2. Цели не зависят от потребителя;

3. Весь доход потребитель тратит на потребление.

Модель потребительского выбора

Задача: максимизировать полезность при ограниченном доходе – ЗМП.

Решением этой задачи будет набор – оптимальный набор, либо локальное рыночное равновесие потребителя.

Рассмотрим систему ограничений задачи:

1. Если на каком-то наборе X бюджетное ограничение выполняется как строгое неравенство, то мы можем увеличить потребление 1го из благ и при этом полезность будет увеличена. (по свойству функции полезности) => будет обращать бюджетное ограничение в равенство .

2. Поскольку функция полезности , , (определена для неотрицательных наборов), то можно сделать вывод, что оптимальный набор будет неотрицательным .

Таким образом, задача может быть сведена к задаче на условный экстремум

𝜆 – неопределенный множитель Лагранжа.

=>

Допустим, система решена решение исходной задачи.

В точке локального рыночного равновесия потребителя выполняются следующие условия.

1. 

Означает, что в этой точке потребитель должен получать одинаковую полезность от последнего рубля, расходуемого на каждое благо.

2. отношение предельных полезностей в этой точке пропорционально рыночным ценам.

3. оценивается как отношение цен на эти блага.

4. все деньги тратятся.

11. Геометрическая интерпретация решения задачи потребительского выбора.

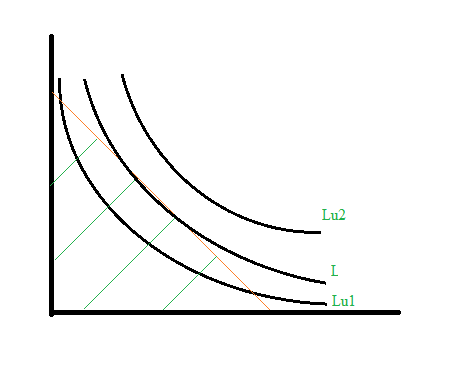
Оптимальное значение будет являться точкой касания бюджетной линии и кривой безразличия.

Любое смещение нарушит равновесие. (стр 23).