
- •Тема 1. Модели и моделирование в экономике
- •Понятие задачи и свойства модели
- •Этапы экономико-математического моделирования
- •Классификация моделей.
- •Экономико-математические дисциплины.
- •Тема 2. Моделирование поведения потребителей и спроса.
- •Пространство потребительских благ.
- •Потребительские предпочтения.
- •Функция полезности.
- •Виды функции полезности и кривых безразличия.
- •Свойства функций полезности.
- •Свойства кривых безразличия
- •Предельная норма замещения благ.
- •Монотонное преобразование функции полезности
- •Бюджетное множество
- •Модель потребительского выбора.
- •Геометрическая интерпретация решения задачи потребительского выбора.
- •Предельная полезность денег.
- •Свойства решения задач потребительского выбора.
- •15) Функция спроса
- •Кривая «доход – потребление»
- •Кривая «цена потребление».
- •16) Эффекты компенсации.
- •Г рафическое представление.
- •17)Уравнение Слуцкого.
- •18) Эластичность функции спроса.
- •Тема 3. Математические модели поведения производителей.
- •Понятие производственной функции
- •Показатели факторов производства – k, l
- •Производственная функция Кобба–Дугласа:
- •Свойства производственной функции:
- •Эластичность производства.
- •Определитель экономической эффективности и масштаба производства.
- •Предельная технологическая норма замещения.
- •Производственная функция с постоянной эластичностью замещения (ces- функция)
- •Тема: поведение фирмы в условиях совершенной конкуренции (ск)
- •Максимизация прибыли в краткосрочном периоде.
- •Минимизация издержек с заданным объемом выпуска.
Максимизация прибыли в краткосрочном периоде.
В краткосрочном периоде есть ряд факторов, значение которое фиксировано. В общем виде это можно представить как функцию ограничений.

Пример:
 – значение второго фактора неизменно
и равно
– значение второго фактора неизменно
и равно
 .
Задача краткосрочного периода имеет
вид:
.
Задача краткосрочного периода имеет
вид:


Для случая с двумя факторами самый простой вид задачи такой:

При
условии:


 – точка
локального рыночного равновесия
производителя в краткосрочном периоде.
Здесь должно быть выполнено условие:
стоимость предельного продукта фактора
равняется его цене.
– точка
локального рыночного равновесия
производителя в краткосрочном периоде.
Здесь должно быть выполнено условие:
стоимость предельного продукта фактора
равняется его цене.
Если фирма максимизирует прибыль и решает производить некоторый объем выпуска y*, то тогда она должна минимизировать издержки производства этого объема выпуска. следовательно задачу можно разделить на 2 шага:
Решается задача минимизации издержек производства любого желаемого объема выпуска.
Определяется какой объем выпуска в действительности является максимизирующим прибыль.
Это разделение позволило сделать несколько полезных выводов.
Минимизация издержек с заданным объемом выпуска.

При ограничении:
f(x1,x2)=q, q- заданная величина. Ее можно решить методом Лагранжа.


Эти функции называются функции условного спроса на факторы производства или функции производного спроса. Они показывают взаимосвязь между ценами фактора и спросом на эти факторы при условии, что фирма производит заданный объем выпуска.
Выводы (1е условие = 2му): если фирма минимизирует издержки, то она выбирает такое сочетание факторов, при котором соблюдается равенство предельных продуктов факторов производства в расчете на единицу xy.
Вывод (смысл множителей Лагранжа):

Если
предположить, что производство увеличится
на 1 единицу, то
 измеряет количество дополнительных
единиц ресурса, необходимого для
производства 1 дополнительной единицы
выпуска. тоже самое можно сказать о 2ом
факторе =>
измеряет количество дополнительных
единиц ресурса, необходимого для
производства 1 дополнительной единицы
выпуска. тоже самое можно сказать о 2ом
факторе =>
 соответствуют дополнительным издержкам
на производство 1ой дополнительной
единицы продукции за счет увеличения
затрат 1ого и 2ого фактора.
соответствуют дополнительным издержкам
на производство 1ой дополнительной
единицы продукции за счет увеличения
затрат 1ого и 2ого фактора.
Модель Лагранжа определяет дополнительные издержки на производство 1ой единицы продукции. Эти издержки по каждому из факторов должны быть одинаковыми в точке оптимального решения.
В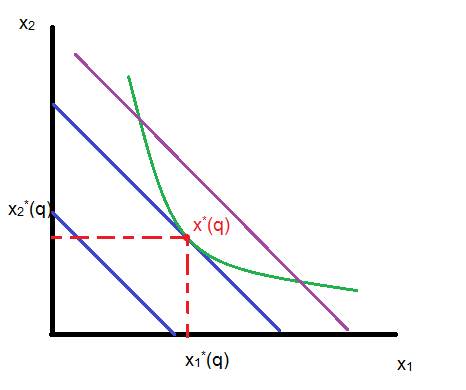 ывод:
ывод:
 продукты должны быть пропорциональными
рыночным ценам, а геометрически это
условие наклона изокванты и изокосты,
т.е.в точке x*
изокванта
касается изокосты.
продукты должны быть пропорциональными
рыночным ценам, а геометрически это
условие наклона изокванты и изокосты,
т.е.в точке x*
изокванта
касается изокосты.
q – тот уровень выпуска, который должны достичь (= ограничение). q- объем выпуска.
С* - минимальные издержки.
 -
функция издержек. Она как минимальные
издержки производства q единиц выпуска
при ценах факторов w1
и w2.
-
функция издержек. Она как минимальные
издержки производства q единиц выпуска
при ценах факторов w1
и w2.
функция условного спроса на рынке не наблюдается. Это условное построение они отвечают на вопрос сколько каждого фактора использовала бы фирма, если бы хотели произвести заданный объем выпуска самым дешевым способом.
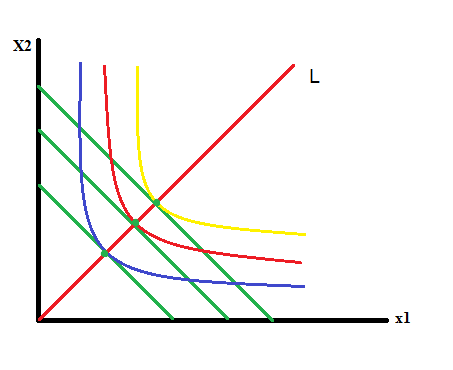
Если
мы будем изменять q =>
 .
Также будет меняться множество точек
x*(q),
вычисленных при разных значениях q,
образуют линию L,
которая
называется долгосрочной линией развития
производства, либо долгосрочным путем
развития/расширения производства.
.
Также будет меняться множество точек
x*(q),
вычисленных при разных значениях q,
образуют линию L,
которая
называется долгосрочной линией развития
производства, либо долгосрочным путем
развития/расширения производства.
В краткосрочном периоде появляется ограничение на объем затрачиваемых ресурсов.






р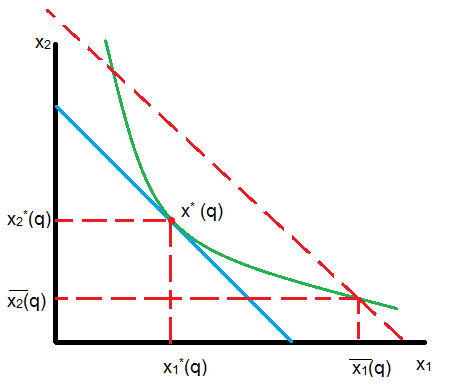 ешение
лежит на …
ешение
лежит на …
 в
краткосрочном периоде издержки
производства всегда возрастают, чем в
долгосрочном. Равны они будут только
в том случае, если
в
краткосрочном периоде издержки
производства всегда возрастают, чем в
долгосрочном. Равны они будут только
в том случае, если
 .
.
Рассмотрим проивоздственную функцию Кобба – Дугласа.



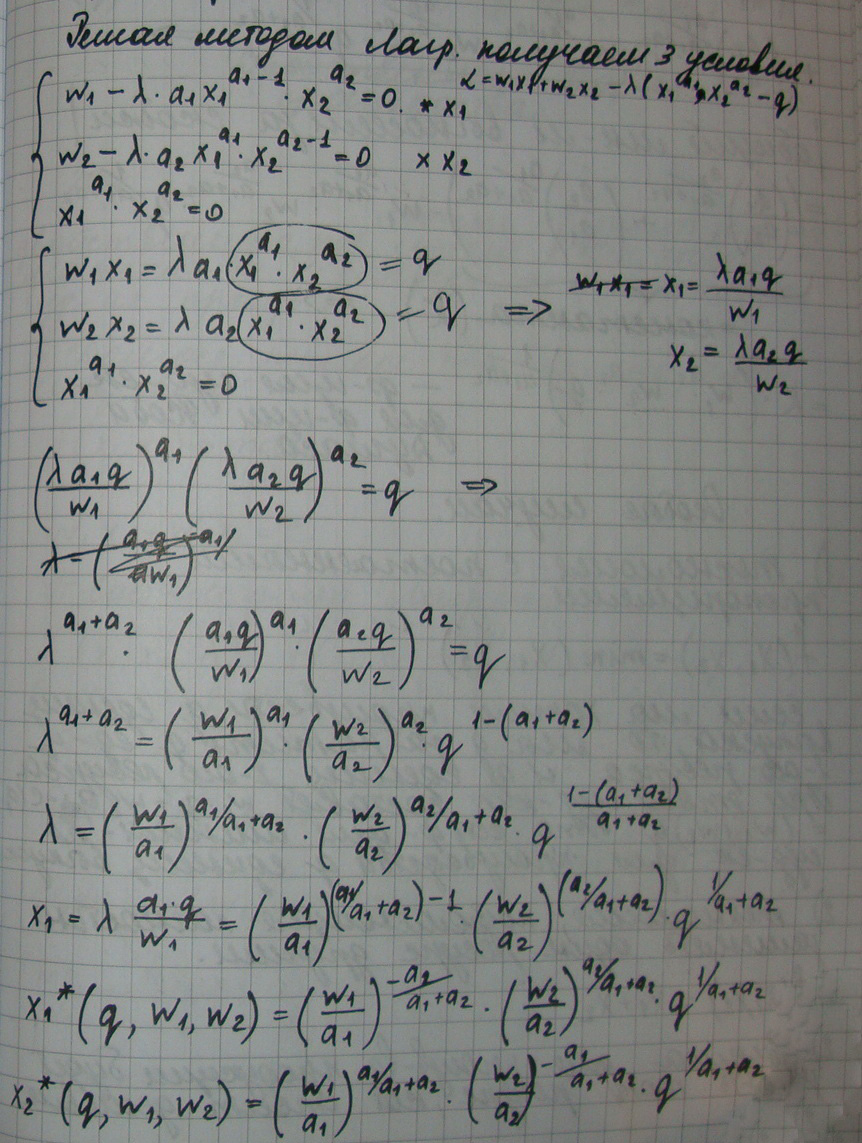
1
¥ - для любого
2
* a - альфа
