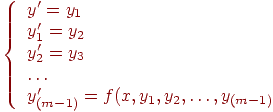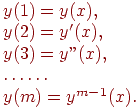- •Содержание
- •Вводная лекция по дисциплине «Методы математического моделирования в теплоэнергетических процессах»
- •Курс "Методы математического моделирования в теплоэнергетических процессах" включает в себя знания, которые являются фундаментальными в системе подготовки инженеров-теплотехников.
- •Дополнительная литература
- •1.2. Форма и принципы представления математической модели
- •1.3. Классификация погрешностей
- •1.4. Классификация алгебраических задач
- •Вопросы для самопроверки
- •Тема 2 Особенности построения математических моделей
- •Вопросы для самопроверки
- •Тема 3 Компьютерное моделирование и вычислительный эксперимент. Решение математических моделей
- •Вопросы для самопроверки
- •Тема 4 Численные методы решения нелинейных уравнений
- •4.1. Метод половинного деления
- •4.2. Метод простых итераций
- •4.3. Метод Ньютона (метод касательных)
- •4.4. Модифицированный метод Ньютона (метод секущих)
- •4.5. Метод хорд
- •Вопросы для самопроверки
- •Тема 5 Компьютерное имитационное моделирование. Статистическое имитационное моделирование
- •Вопросы для самопроверки
- •Тема 6 Компьютерное моделирование и решение линейных и нелинейных многомерных систем
- •6.1. Решение систем линейных уравнений методом Гаусса
- •Вопросы для самопроверки
- •Тема 7 Моделирование многомерных нелинейных систем
- •7.1. Решение систем нелинейных уравнений
- •7.2. Метод простых итераций
- •7.3. Решение систем нелинейных уравнений методом Ньютона
- •7.4. Определение матрицы Якоби
- •Вопросы для самопроверки
- •Тема 8 Компьютерное моделирование при обработке опытных данных
- •8.1. Интерполяции и экстраполяция
- •8.2. Построение интерполяционного многочлена в явном виде
- •8.3. Интерполяция по Лагранжу
- •8.4. Программирование формулы Лагранжа
- •8.5. Интерполяция по Ньютону
- •8.6. Разделенные разности
- •8.7. Программирование формулы Ньютона
- •8.8. Пример интерполяции по Ньютону
- •8.9. Сплайн-интерполяция
- •8.10. Аппроксимация опытных данных
- •8.11. Сглаживание опытных данных методом наименьших квадратов
- •8.12. Программирование метода наименьших квадратов (мнк)
- •Вопросы для самопроверки
- •Тема 9 Компьютерное моделирование и решение нелинейных уравнений
- •9.1. Метод прямоугольников
- •9.2. Метод трапеций
- •9.3. Метод Симпсона
- •9.4. Численные методы решения дифференциальных уравнений первого порядка
- •9.5. Методы Рунге - Кутта
- •9.6. Метод Рунге - Кутта 2-го порядка (модифицированный метод Эйлера)
- •9.7. Метод Рунге - Кутта 4-го порядка
- •9.8. Решение дифференциальных уравнений высоких порядков
- •9.9. Решение дифференциальных уравнений второго порядка
- •9.10. Решение дифференциальных уравнений m-го порядка методом Рунге-Кутта (4-го порядка)
- •Вопросы для самопроверки
9.10. Решение дифференциальных уравнений m-го порядка методом Рунге-Кутта (4-го порядка)
Как уже было сказано, любое дифференциальное уравнение m-го порядка
|
(9.15) |
сводится к системе, состоящей из m дифференциальных уравнений 1-го порядка
|
(9.6) |
Численным решением системы (9.9), а значит и дифференциального уравнения m-го порядка (9.8) является m табличных функций
![]()
т.е. функция y(x) и все ее производные, включая производную (m-1)-го порядка.
При этом каждая из табличных функций
определяется на промежутке [a, b] с шагом
h и включает n узловых точек. Таким
образом, численным решением уравнения
(9.8) или системы (9.9) является матрица
порядка
![]() ,
(табл. 9.8)
,
(табл. 9.8)
i |
x |
y |
y1=y', |
y1=y''1, |
: |
y_m-1=y^(m-1) |
0 |
x0 |
y0 |
(y1)0 |
(y2)0 |
: |
(ym-1)0 |
1 |
x1 |
y1 |
(y1)1 |
(y2)1 |
: |
(ym-1)1 |
2 |
x2 |
y2 |
(y1)2 |
(y2)2 |
: |
(ym-1)2 |
3 |
x3 |
y3 |
(y1)3 |
(y2)3 |
: |
(ym-1)3 |
: |
: |
: |
: |
: |
: |
: |
n |
xn |
yn |
(y1)n |
(y2)n |
: |
(ym-1)n |
где
m - порядок дифференциального уравнения, равен количеству столбцов матрицы,
n = (b-a)/h - количество шагов интегрирования, равно количеству строк матрицы.
Каждый j-й столбец матрицы - это массив решений одной j-й табличной функции по всем n шагам интегрирования.
Каждая i-ая строка матрицы - это массив решений m табличных функций на одном i-ом шаге интегрирования.
На графике решением дифференциального уравнения m-го порядка (9.8) является совокупность узловых точек. При этом каждому шагу интегрирования, т.е. каждому значению xi, , соответствуют m узловых точек скоординатами
![]()
При построении алгоритма задачи будем как и ранее расчет вести по шагам интегрирования, т.е. в цикле по . При этом, как и ранее, на каждом i-ом шаге цикла будем рассчитывать решение дифференциального уравнения и тут же его печатать. Тогда нет необходимости формировать матрицу решений, а можно ограничиться формированием массива решений (9.15), который соответствует одной i-й строке матрицы:
|
(9.17) |
где
|
(9.18) |
Тогда при построении системы дифференциальных уравнений изменится индексация.
Рассмотрим пример (9.19).
Дано дифференциальное уравнение второго порядка
|
(9.19) |
С учетом обозначений (9.18) имеем:
![]()
Тогда дифференциальное уравнение (9.19) сводится к системе:
|
(9.20) |
Вычисление правых частей уравнений системы (9.20) будем выполнять в подпрограмме PRAV. При этом подпрограмма PRAV будет иметь вид
![]()
Обращение к подпрограмме
PRAV(m, x, Y, F),
где
m-порядок системы,
x- значение x на i-м шаге интегрирования,
Y=[y(1), y(2), y(3), : , y(m)] - входной массив длиной m,
F=[f(1), f(2),:, f(m)] - результат, массив значений правых частей уравнений системы (9.10) длиной m.
Программу решения системы дифференциальных уравнений реализуем в виде 3-х программных модулей:
- основной программы, в которой организуем циклический процесс по всем шагам интегрирования, ;
- подпрограммы RGK, в которой на каждом
i-м шаге реализуется метод Рунге Кутта
(4-го порядка) для системы дифференциальных
уравнений m-го порядка. Здесь на каждом
шаге интегрирования вычисляется массив
решений Y длиной m. Для этого внутри
подпрограммы RGK организуем циклы по j,
где
![]() ;
;
- подпрограммы PRAV, обращение к которой осуществляется из подпрограммы RGK для вычисления массива F длиной m - значений правых частей уравнений системы.
Схема алгоритма основной программы представлена на рис.9.17.
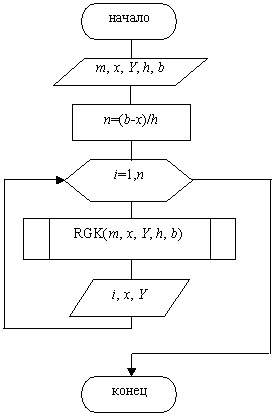
Рис. 9.17. Схема алгоритма основной программы
Здесь
m-порядок системы,
h-шаг интегрирования,
n-количество шагов интегрирования,
x-начальное и далее - текущее значение x,
Y-массив длинной m, куда заносим начальные и далее - текущие значения решений системы на одном шаге интегрирования.
В подпрограмме RGK для вычисления элементов массива Y, используем те же формулы, что и для решения одного дифференциального уравнения 1-го порядка методом Рунге-Кутта (4-го порядка), но с учетом поправки на массивы.
Тогда
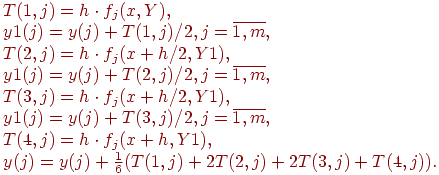
Здесь
Y- массив решений длиной m,
Y1 - рабочий массив длиной m,
T - рабочая матрица порядка (![]() ).
).
Для вычисления значений fj правых частей дифференциальных уравнений системы перед вычислением каждого элемента матрицы Т на каждом j-ом шаге необходимо выполнить обращение к подпрограмме PRAV.
Схема алгоритма подпрограммы RGK представлена на рис.9.18
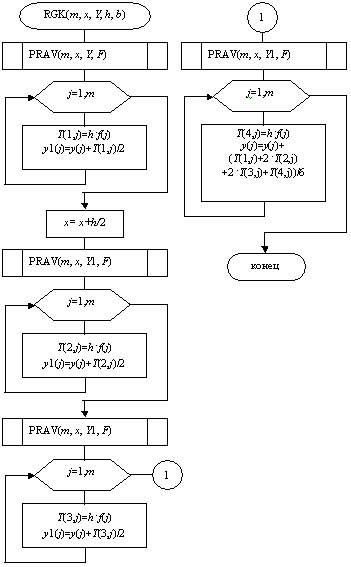
Рис. 9.18. Схема алгоритма подпрограммы RGK