9.1. Метод прямоугольников

Словесный алгоритм метода прямоугольников:

1. Весь участок [a,b] делим на n равных частей с шагом h=(b-a)/n.

2. Определяем значение y_i подынтегральной функции f(x) в каждой части деления, т.е.

3. В каждой части деления подынтегральную функцию f(x) аппроксимируем интерполяцион-ным многочленом степени n = 0, т.е. прямой, параллельной оси OX. В результате вся подынтегральная функция на участке [a,b] аппроксимируется ломаной линией.

4. Для каждой части деления определяем площадь S_i частичного прямоугольника.

5. Суммируем эти площади. Приближенное значение интеграла I равно сумме площадей частичных прямоугольников.

Если высота каждого частичного прямоугольника равна значению подынтегральной функции в левых концах каждого шага, то метод называется методом левых прямоугольников (рис.9.3). Тогда квадратурная формула имеет вид

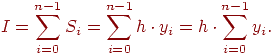
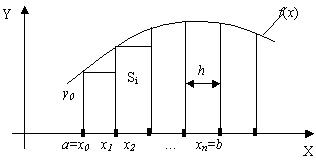
Рис. 9.3.  Метод левых прямоугольников

Если высота каждого частичного прямоугольника равна значению подынтегральной функции в правых концах каждого шага, то метод называется методом правых прямоугольников (рис.9.4). Тогда квадратурная формула имеет вид

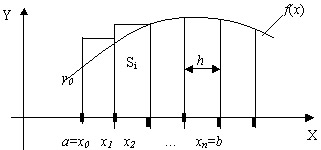
Рис. 9.4.  Метод правых прямоугольников

Точность каждого метода прямоугольников имеет порядок h.

Алгоритм вычисления интеграла построим в виде итерационного процесса поиска с автоматическим выбором шага. На каждом шаге будем уменьшать шаг в два раза, то есть увеличивать число шагов n в два раза. Выход из процесса поиска организуем по точности вычисления интеграла. Начальное число шагов n=2.Схема алгоритма методов прямоугольников представлена на рис.9.5.

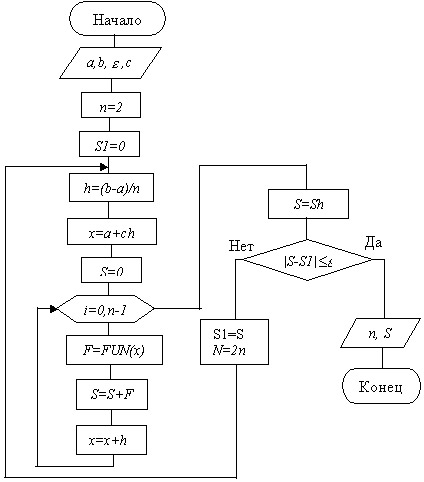
Рис. 9.5.  Схема алгоритма метода прямоугольников (с автоматическим выбором шага)

Условные обозначения:

a,b - концы интервала,

- заданная точность,

с=0 - метод левых прямоугольников,

с=1 - метод правых прямоугольников,

S1 - значение интеграла на предыдущем шаге,

S - значение интеграла на текущем шаге.

9.2. Метод трапеций

Словесный алгоритм метода трапеций:

1. Интервал [a,b] делим на n равных частей с шагом h=(b-a)/n.

2. Вычисляем значение подынтегральной функции в каждой узловой точке

3. На каждом шаге подынтегральную функцию f(x) аппроксимируем прямой, соединяющей две соседние узловые точки. В результате вся подынтегральная функция на участке [a,b] заменяется ломаной линией проходящей через все узловые точки.

4. Вычисляем площадь каждой частичной трапеции.

5. Приближенное значение интеграла равно сумме площадей частичных трапеций, т.е. .

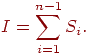Найдем площади S_i частичных трапеций:

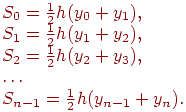
Приближенное значение интеграла равно

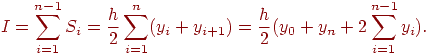
Точность метода трапеций имеет порядок h².

Схема алгоритма метода трапеций представлена на рис.9.6.

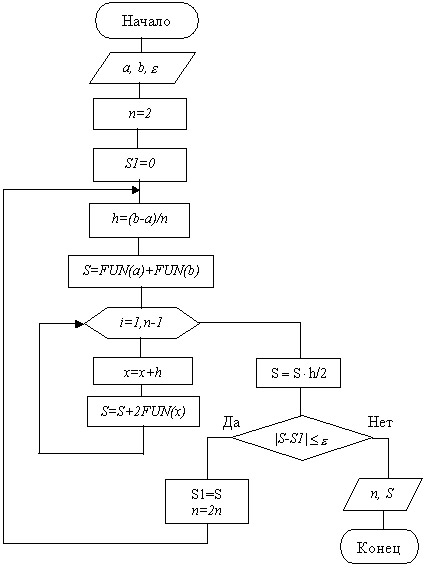
Рис. 9.6.  Схема алгоритма метода трапеций (с автоматическим выбором шага)

9.3. Метод Симпсона

В методе Симпсона в каждой части деления подынтегральная функция аппроксимируется квадратичной параболой a₀x²+a₁x+a₂. В результате вся кривая подынтегральной функции на участке [a,b] заменяется кусочно-непрерывной линией, состоящей из отрезков квадратичных парабол. Приближенное значение интеграла I равно сумме площадей под квадратичными параболами.

Т.к. для построения квадратичной параболы необходимо иметь три точки, то каждая часть деления в методе Симпсона включает два шага, т.е.

L_k=2h.

В результате количество частей деления N2=n/2. Тогда n в методе Симпсона всегда четное число.

Определим площадь S₁ на участке [x₀, x₂] (рис.9.2).

Исходя из геометрического смысла определенного интеграла, площадь S₁ равна определенному интегралу от квадратичной параболы на участке [x₀, x₂]:

Неизвестные коэффициенты квадратичной параболы а₀ , а₁, а₂ определяем из условия прохождения параболой через три узловых точки с координатами (x₀y₀), (x₁x₁), (x₂y₂).

На основании этого условия строим систему линейных уравнений:

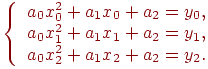
Решая эту систему, найдем коэффициенты параболы.

В результате имеем: .

Для участка [x₂, x₄]: .

:::::::::::::::::::

Для участка [x_i-1, x_i+1]: ,

где

Суммируя все площади S₁ под квадратичными параболами, получим квадратурную формулу по методу Симпсона:

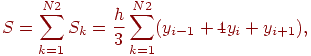
где

N2 - количество частей деления.

Точность метода Симпсона имеет порядок (h³/h⁴).

Схема алгоритма метода Симпсона представлена на рис.9.7.

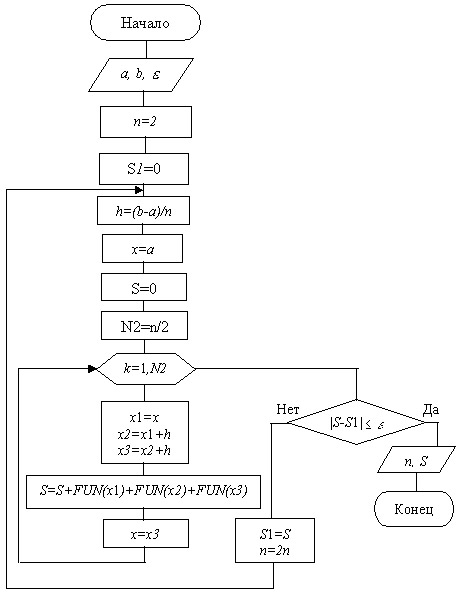
Рис. 9.7.  Схема алгоритма Симпсона (с автоматическим выбором шага)