4.1.3 Пересечение многогранников проецирующей плоскостью

Если многогранник рассечь плоскостью, то линия пересечения поверхности многогранника с плоскостью будет замкнутой плоской ломаной линией, т.е. многоугольником.

Каждая вершина этого многоугольника есть точка, в которой плоскость пересекла его ребро.

Каждая сторона этого многоугольника есть отрезок прямой линии, по которой плоскость пересекла грань многоугольника.

Для того чтобы построить линию пересечения плоскости с поверхностью многогранника необходимо:

1. Найти точки пересечения ребер многогранника с секущей плоскостью.

2. Соединить полученные точки отрезками. В результате этого получают стороны многоугольника, лежащего в плоскости пересекающей многогранник.

На рисунках 20 и 21 показаны примеры пересечения треугольной призмы и четырехугольной пирамиды плоскостями различного положения.

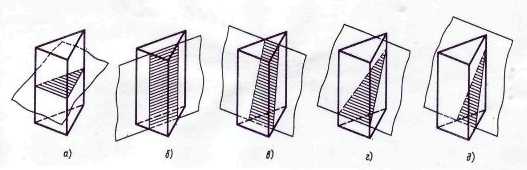
Рисунок 20

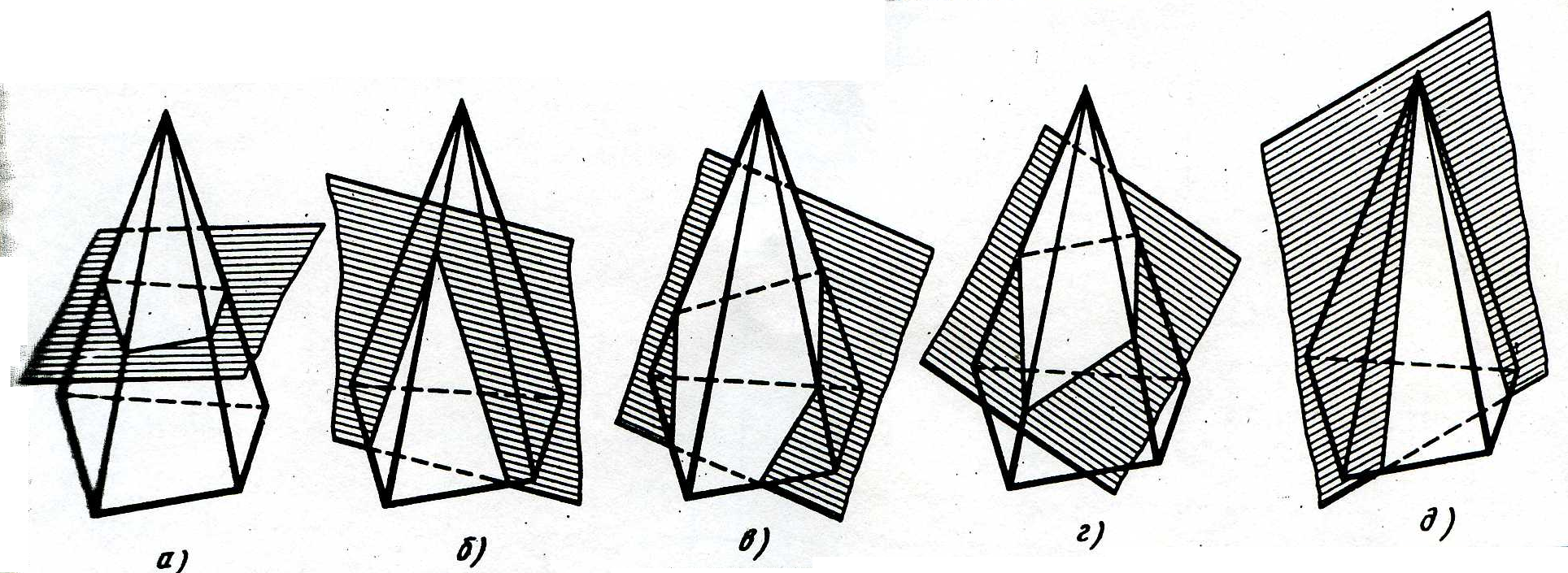
Рисунок 21

4.2 Контрольное задание №3

Построить комплексный чертеж усеченного тела.

В состав комплексного чертежа входят:

- ортогональные проекции;

- натуральная величина фигуры среза;

- развертка;

- прямоугольная изометрия.

4.2.1 Указания к решению контрольного задания

(Образец выполнения - рисунок 22)

1. Задание выполняется на формате А3;

2. Условия задачи даны в таблице 3;

3. В левой части формата строим 3 вида фигуры;

4. Призма пересечена фронтально-проецирующей плоскостью ;

5. Отсеченную часть призмы на проекциях и развертке изобразим тонкими линиями, а оставшуюся часть усеченной призмы обведем сплошной основной линией;

6. Т.к. плоскость перпендикулярна П₂, она спроецируется на эту плоскость в прямую линию. На эту же линию спроецируется и фигура среза, лежащая в плоскости .

7. Фигура среза на горизонтальной проекции совпадает с проекцией основания и изображается как правильный шестиугольник, т.к. линии среза принадлежат боковым граням призмы.

8. Используя линии проекционной связи, строим срез на П₃.

9. Ни на одной из 3-х плоскостей проекций фигура среза не проецируется в натуральную величину, т.к. плоскость в которой она лежит, не параллельна ни одной из плоскостей проекций.

10. Строим натуральную величину фигуры среза методом вращения (рисунок 19) или методом перемены плоскостей проекций (рисунок 15).

11. Строим развертку усеченного тела:

- проводим прямую, на которой откладываем 6 отрезков, равных натуральной длине сторон основания (размеры берем с П₁);

- из полученных точек проводят прямые, перпендикулярные данной прямой;

- на проведенных перпендикулярах, откладываем длины соответствующих усеченных ребер, измеренных на П₂ или П₃;

- полученные точки соединяют отрезками и получаем ломаную линию среза;

- вычерчиваем основание и натуральную величину среза.

12. Построение прямоугольной изометрической проекции:

- строим оси; они располагаются под углом 120º друг к другу;

- вычерчиваем основание шестиугольника в осях ХОУ (размеры берем с П₁);

- из вершины проводим линии параллельные оси Z;

- на этих линиях откладываем длины усеченных ребер (измеряем их длину на П₂ или П₃);

- соединяем полученные точки и обводим фигуру с учетом видимости.

Таблица 3 - Исходные данные к контрольному заданию № 3

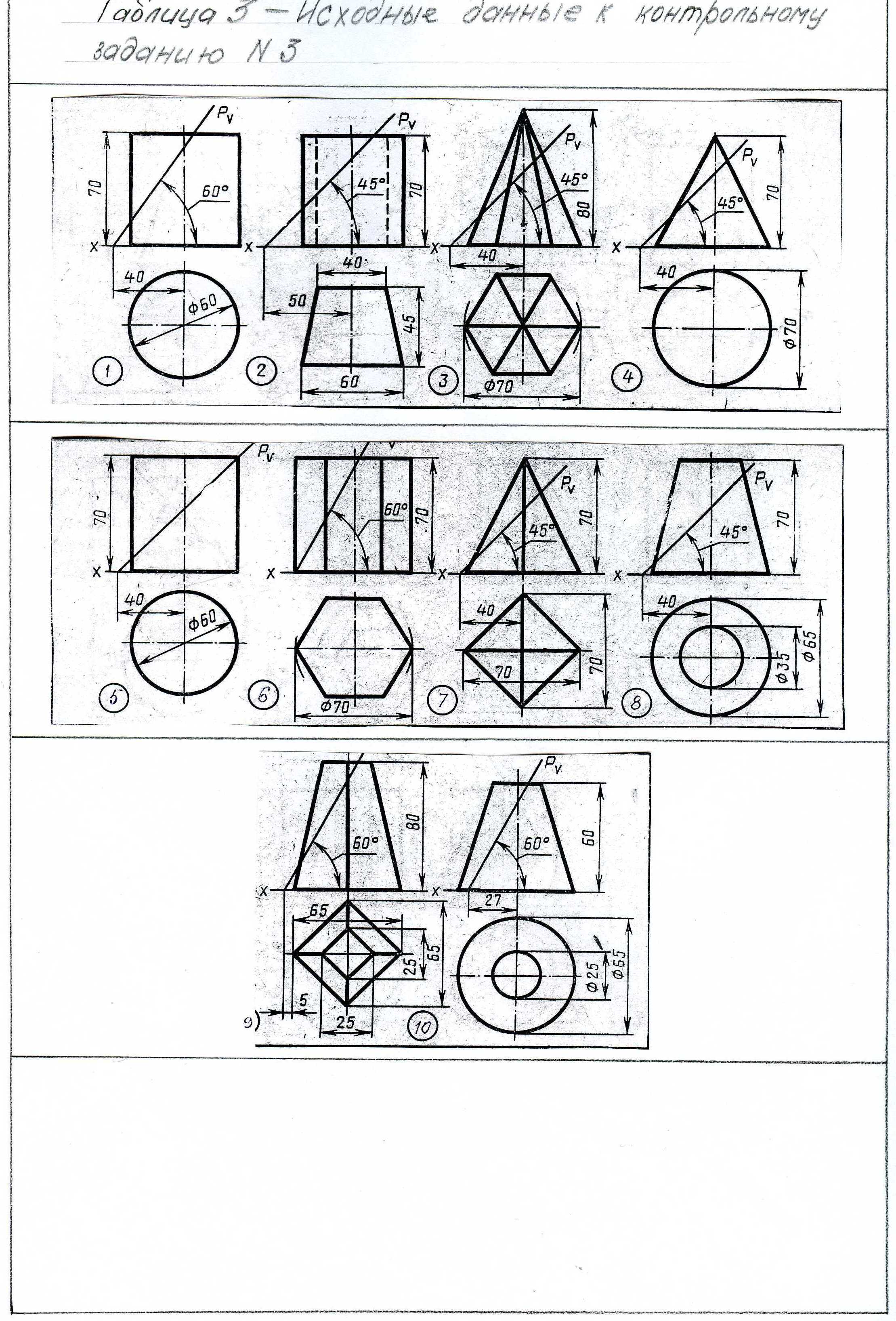
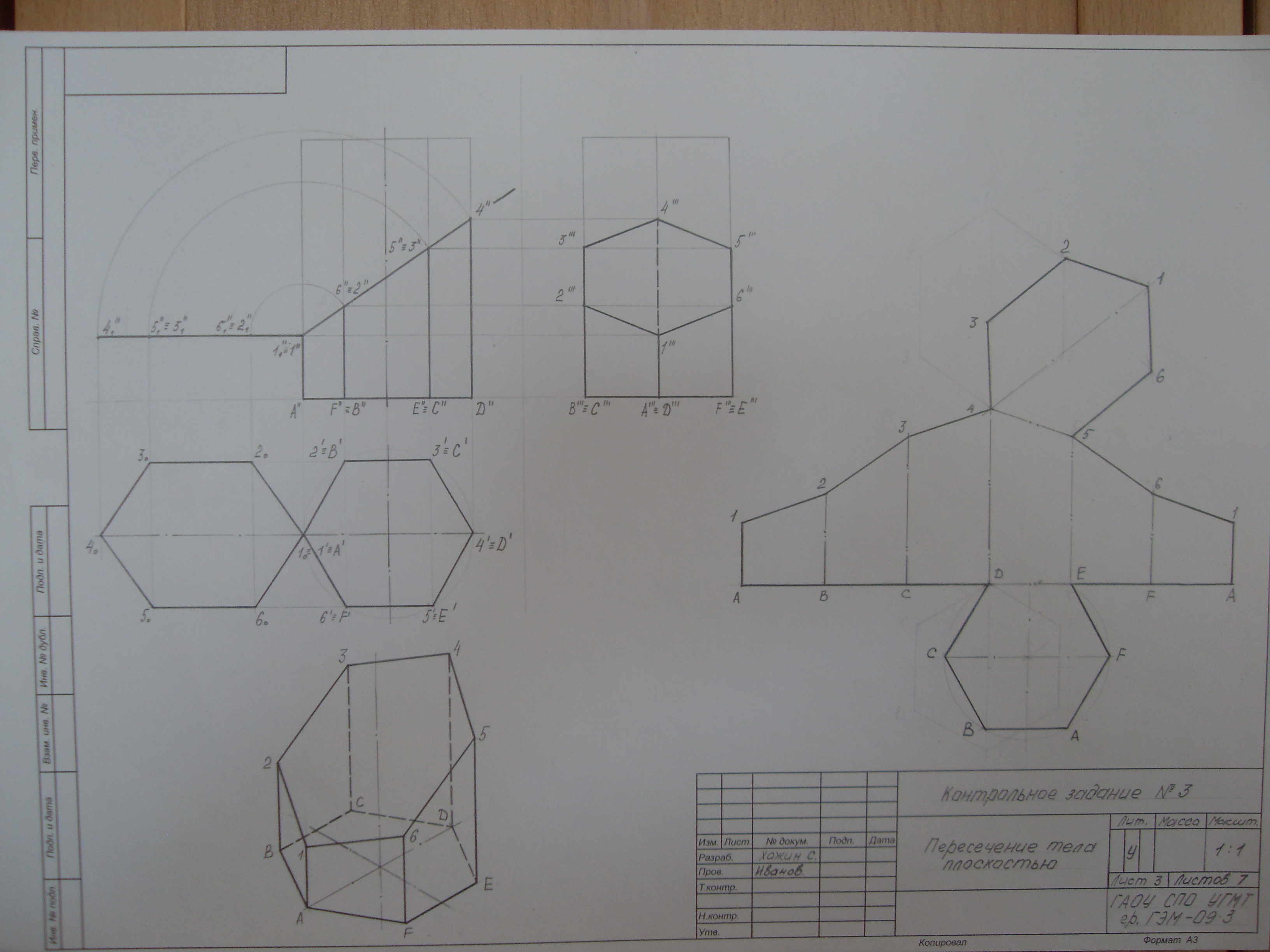
Рисунок 22