2 Геометрические построения. Сопряжения

2.1 Деление окружности на равные части

2.1.1 На 3 части (рисунок 4)

Рисунок 4

Из точки А , проводим дугу, равную радиусу окружности. Получаем точки 1 и 2.

Третья точка будет находиться на противоположном конце диаметра, проходящего через точку А.

2.1.2 На 5 частей (рисунок 5)

Рисунок 5

2.1.3 На 6 частей (рисунок 6)

Рисунок 6

2.1.4 На 8 частей (рисунок 8)

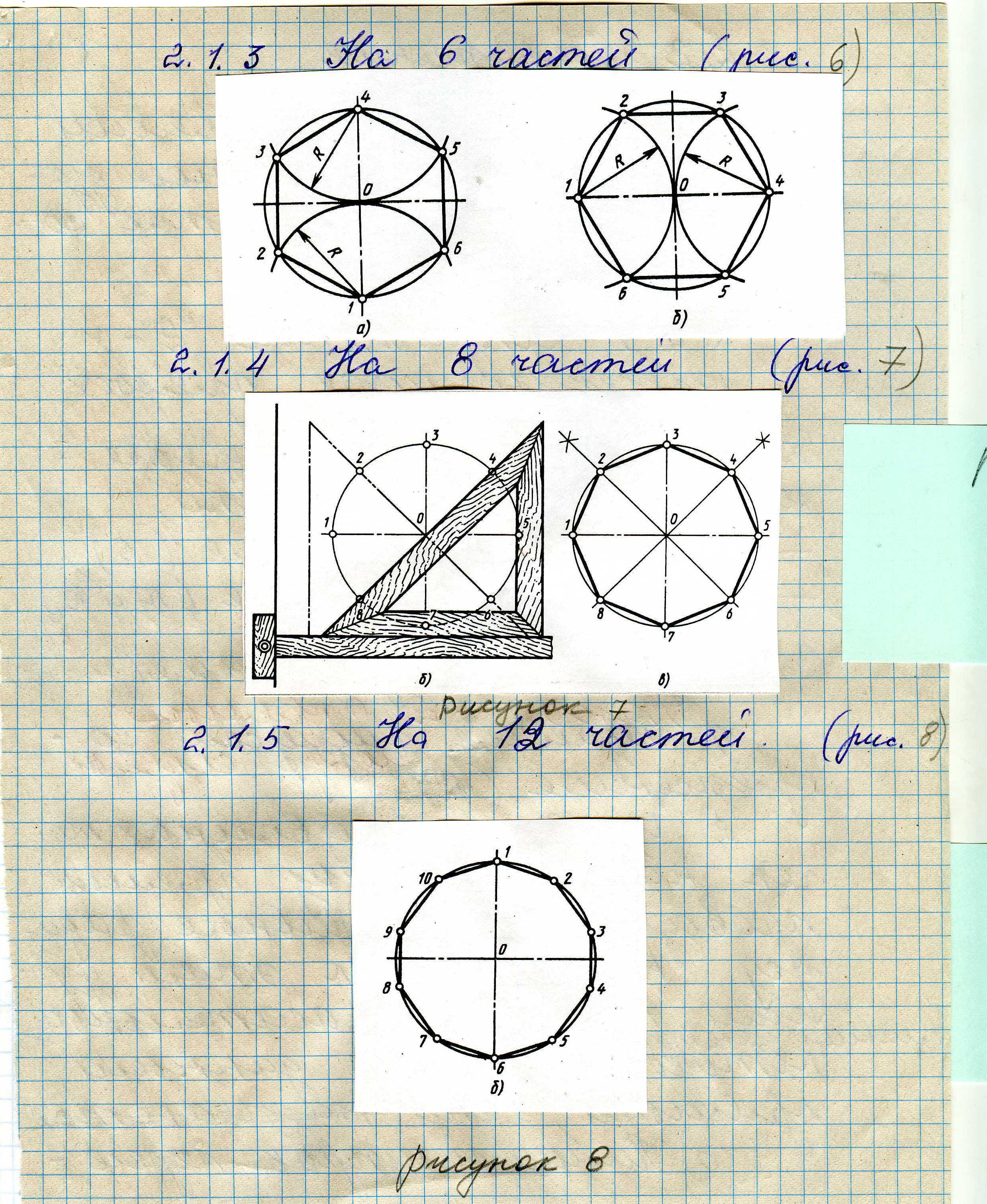
Рисунок 7

2.1.5 На 12 частей (рисунок 8)

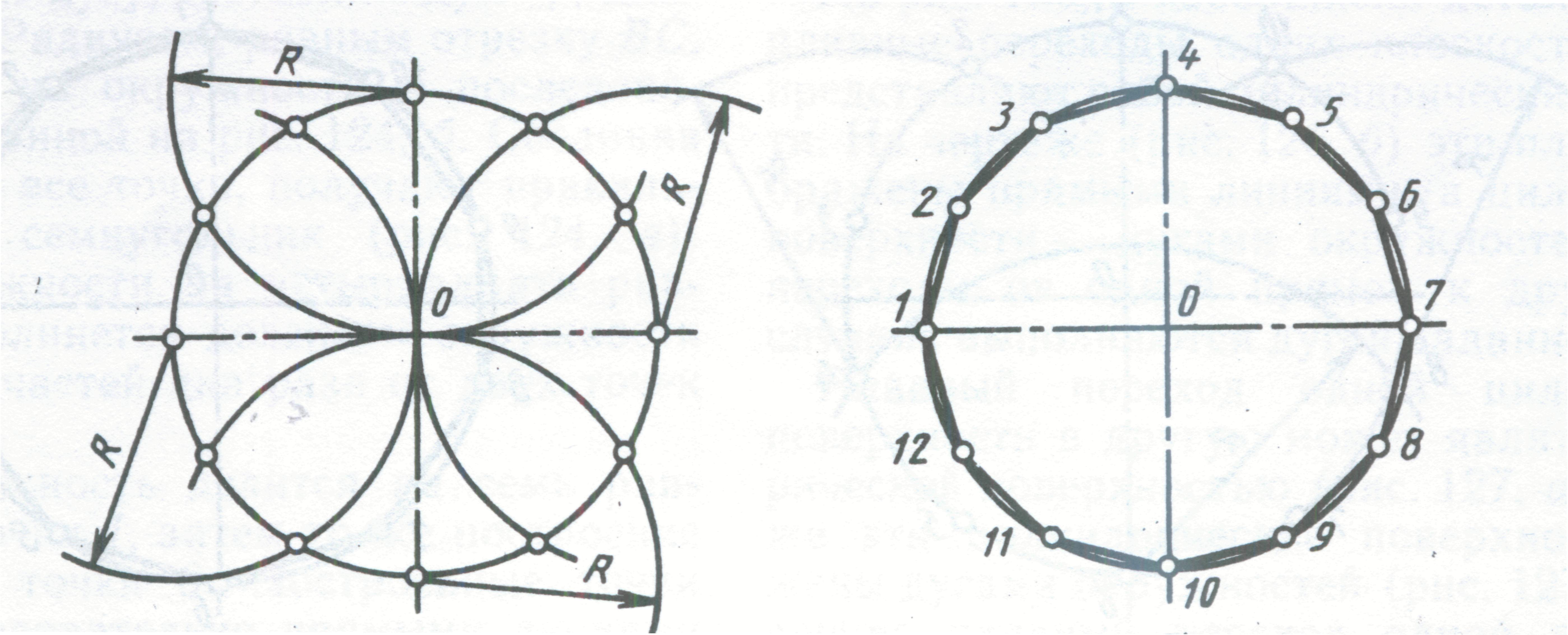
Рисунок 8

2.2 Сопряжения

Плавный переход прямой линии в дугу или одной дуги в другую, называется сопряжением.

2.2.1 Сопряжение двух пересекающихся прямых

Для построения сопряжения необходимо найти:

- центр сопряжения (О) ;

- точки сопряжения (К и К₁).

Дано:

- 2 ∩ прямые

- радиус сопряжения.

Построение сопряжения (рисунок 9)

1. Провести параллельно заданных прямых линии центров на расстоянии равном радиусу R дуги сопряжения.

2. Точка пересечения данных линий будет центром дуги сопряжения (О).

3. Для нахождения точек сопряжения К и К₁ необходимо опустить из центра О перпендикуляры на заданные прямые.

4. Зная центр и точки сопряжения из точки О радиусом R проводят дугу сопряжения.

Рисунок 9

2.2.2 Сопряжение дуги с прямой линией (рисунок 10)

Дано:

- окружность радиусом R;

- прямая;

- радиус сопряжения R₁.

Построение сопряжения

1) Нахождение центра дуги сопряжения Q₁:

а) параллельно заданной прямой на расстоянии равном радиусу сопряжения R₁ проводим линию центра;

б) из центра окружности О проводим вспомогательную дугу радиусом R+R₁;

в) пересечение данных линий центров (точка О₁) является центром дуги сопряжения.

2) Нахождение точек сопряжения:

а) на прямой:

- из О₁ опускаем ┴ на прямую, получаем точку К;

б) на дуге:

- соединяем центры О и О₁

- точка пересечения К₁ находится на пересечении данной прямой с заданной окружностью.

Рисунок 10

2.2.3 Сопряжение 2-х окружностей дугой заданного радиуса

Дано:

- две окружности с центрами О и О₁ и радиусами R и R₁

- радиус сопряжения R₂ .

А) Построение внешнего сопряжения (рисунок 11)

1) Из центра О проводим вспомогательную дугу радиусом R+R₁;

2) Из центра О1 проводим вспомогательную дугу радиусом R₁+R₂ .

3) Точка пересечения двух вспомогательных дуг О₂ является центром сопряжения.

4) Для нахождения точек сопряжения необходимо соединить точку О₂ с точками О и О₁.

5) Точки пересечения данных линий с заданными окружностями будут являться точками сопряжения К и К₁.

6) Из центра О₂ проводим дугу сопряжения радиусом R₂, соединяя точки К и К₁ .

Рисунок 11

Б) Построение внутреннего сопряжения (рисунок 12)

1) Из центра О проводим вспомогательную дугу R₃=R₂-R

2) Из центра О₁ проводим вспомогательную дугу радиусом R₄=R₂-R₁

3) Вспомогательные дуги пересекутся в точке О₂, являющейся центром сопряжения.

4) Для построения точек сопряжения К и К₁:

- из О₂ через центры О и О₁ проводим лучи до пересечения их с заданными окружностями, получаем точки К и К₁.

5) Из центра О₂ проводим дугу сопряжения радиусом R₂ соединяя точки К и К₁.

Рисунок 12