Гипотеза совпадения двух независимых средних величин
Из двух
независимых экспериментов получены
две группы результатов многократных
измерений x1,
x2,
…, xn1
и y1,
y2,
…, yn2
нормально распределенных величин x
и y.
После обработки найдены оценки
,
и
,
.
Проверяется гипотеза о том, что
.
Введем новую величину
(43)
Если
равенство
справедливо
для
и
,
то при конечных значениях количеств
измерений n1
и n2
распределение величины t
близко
к распределению Стьюдента, у которого
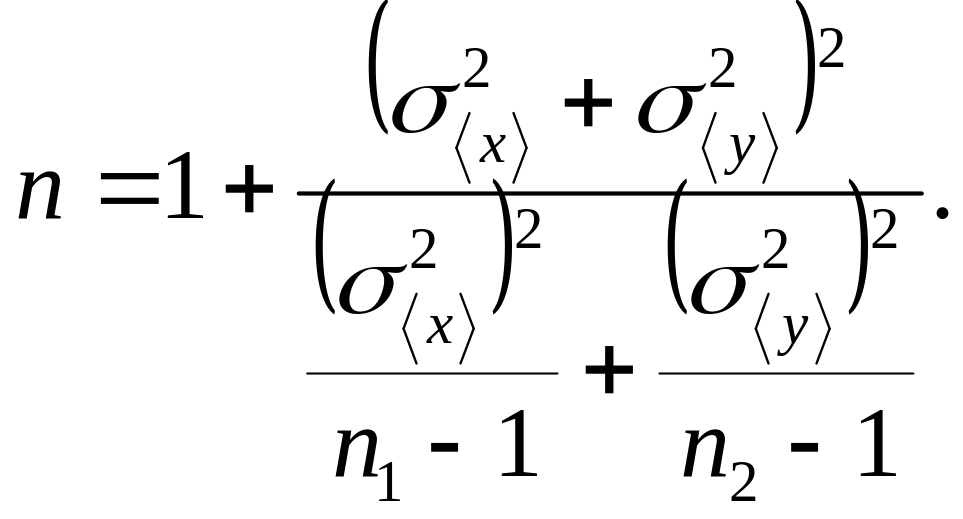(44)
При уровне
значимости α гипотеза
подтверждена,
если
,
чему соответствует доверительная
вероятность α.
Гипотеза о линейности данных
После определения значений параметров с помощью метода наименьших квадратов необходимо проверить справедливость гипотезы о том, что экспериментально зарегистрированная зависимость является линейной в некоторых координатах. Фактически речь идет о верификации (проверке справедливости) используемого модельного описания. Обратимся к выражению, задающему остаточную сумму квадратов:
(45)
где в качестве a и b использованы их экспериментальные оценки, σi – дисперсия отдельного измерения. В статистике обосновывается, что величина . подчиняется распределению χ2 (читается «кси-квадрат»), плотность вероятности которого
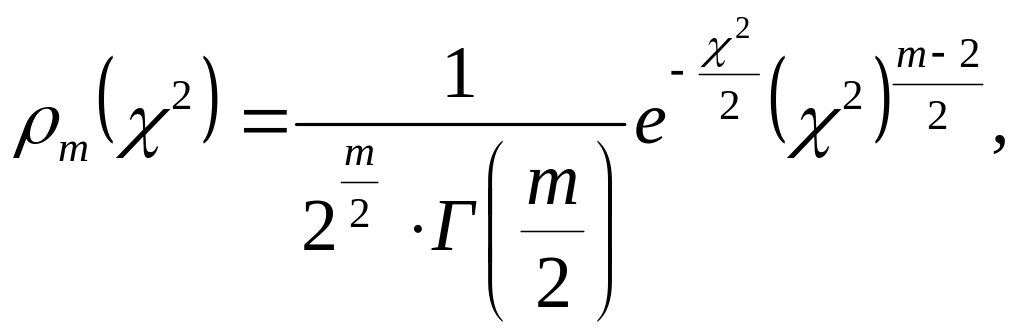(46)
где 0 <
<
,
а (n
–
количество парных измерений). Для
распределения характерно совпадение
среднего значения и индекса m.
Анализ гипотезы
о справедливости интерпретации
экспериментальной зависимости, как
линейной, начинают с введения уровня
значимости α,
задающего интервал от 0 до
,
в который величина φ
попадает,
если гипотеза справедлива. Для вычисления
необходимо решить уравнение
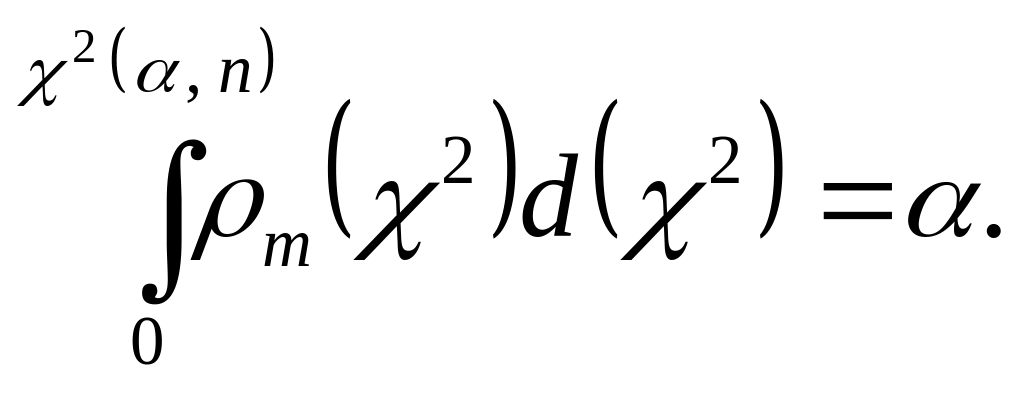(47)
Величины приведены в табл. 5.
Таблица №5
Границы интервалов для уровня значимости α (n – количество парных измерений)
-
n
Α
0,75
0,95
0,99
0,999
4
1,3
3,8
6,6
10,8
5
2,8
6,0
9,2
13,8
6
4,1
7,8
11,3
16,3
7
5,4
9,5
13,3
18,5
8
6,6
11,0
15,1
20,5
9
7,8
12,6
16,8
22,5
10
9,0
14,1
18,5
24,3
11
10,2
15,5
20,1
26,1
12
11,4
16,9
21,7
27,9
13
12,6
18,3
23,2
29,6
14
13,7
19,7
24,7
31,3
15
14,9
21,0
26,2
32,9
16
16,0
22,4
27,7
34,6
17
17,1
23,7
29,1
36,1
18
18,3
25,0
30,6
37,7
19
19,4
26,3
32,0
39,3
20
20,5
27,6
33,4
40,8
30
31,5
40,1
47,0
55,5
50
56,0
68,0
76,0
87,0
100
109
124
136
149
Если неравенство
<
не
выполнено,
то гипотеза о линейности отвергается.
Вместе с тем возможны другие причины
несоблюдения неравенства – необходимо
проверить положения, при которых
правомерно применение метода наименьших
квадратов.
Иногда возникает ситуация, когда нет сведений о погрешности отдельных измерений. В этом случае для проверки гипотезы линейности можно использовать величину
(48)
где n – число измерений, R – коэфициент корреляции Пирсона, безразмерный индекс в интервале от –1,0 до 1,0 включительно, который отражает степень линейной зависимости между двумя множествами данных:
(49)
В статистике обосновывается, что величина λ подчиняется t–распределению с n–2 степенями свободы. При выполнении условия λ < гипотеза о линейной зависимости отвергается.