Министерство образования Российской Федерации

Федеральное государственное бюджетное

образовательное учреждение

высшего профессионального образования

Московский государственный технологический

университет "СТАНКИН"

Егорьевский технологический институт (филиал)

РЕШЕНИЕ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ В СИСТЕМЕ МATHCAD.

Методические указания

к выполнению лабораторной работы

ЕТИ.ПМ.01

Егорьевск 2012

Составитель: кандидат физ.-мат. наук, доцент Т.В. Бармакова

Данные указания предназначены для студентов, обучающихся по специальности 120100. В методических указаниях приведено содержание и изложен порядок выполнения лабораторной работы по теме «Решение обыкновенных дифференциальных уравнений в системе Мathcad.».

Методические указания рассмотрены и одобрены кафедрой естественнонаучных дисциплин.

Протокол № от

Зав. кафедрой ________________А.П. Нилов

Методические указания рассмотрены и одобрены методическим советом института

Протокол № от

Председатель совета_______________ Семенов А.Д.

Решение обыкновенных дифференциальных уравнений в системе Мathcad.

Цель работы: 1) Изучить решение дифференциальных уравнений 1-го порядка с разделяющимися переменными в системе Mathcad 2) Изучить решение дифференциальных уравнений и систем в нормальной форме численным методом Рунге-Кутты в системе Мathcad.

Решение дифференциальных уравнений.

Краткие сведения из теории.

1. Дифференциальные уравнения первого порядка.

Обыкновенным дифференциальным уравнением первого порядка называется уравнение

,

где F – известная функция трех переменных, определенная в области GR³; х – независимая переменная из интервала (а,b), у=у(х) – неизвестная функция; -- ее производная.

Функция у=у(х) называется решением дифференциального уравнения, если она при всех x(a,b) удовлетворяет уравнению

.

График решения дифференциального уравнения называют интегральной кривой дифференциального уравнения. В дальнейшем будем рассматривать обыкновенные дифференциальные уравнения, разрешенные относительно производной, т.е. уравнения в нормальной форме:

.

Если дифференциальное уравнение первого порядка , (х,у)G , имеет в области G решение , то , вообще говоря, таких решений бесконечно много , они могут быть заданы в виде y=y(x,C), где С – произвольная константа, такая , что (х, y(x,C)) )G и при произвольных значениях С. Однако, если поставить задачу – найти решение , удовлетворяющее начальному условию у₀=у(х₀) , то при определенных условиях такая задача имеет единственное решение. Задача об отыскании решения дифференциального уравнения, удовлетворяющему заданному начальному условию , называется задачей Коши.

Рассмотрим задачу Коши . Если функции f(x,y) и ее частная производная непрерывны в области G, (х₀, у₀) G , то на некотором интервале (х₀-h,x₀+h) существует единственное решение уравнения, удовлетворяющее заданному начальному условию.

Для уравнения с разделяющимися переменными, имеющего вид

выражение

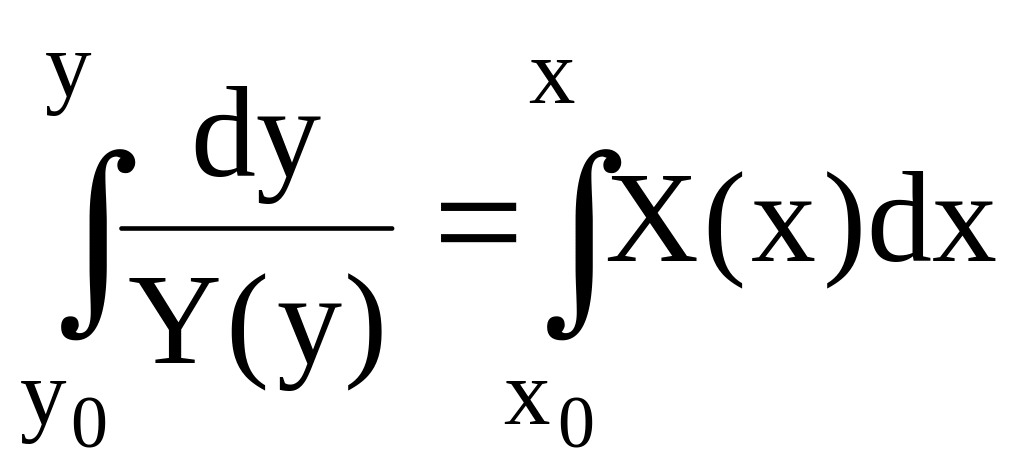
задает решение y=y(x) задачи Коши с начальным условием у₀=у(х₀) как функцию переменной х , неявно.

Пояснения к выполнению задания № 1.

Найдите решение уравнения с разделяющимися переменными , удовлетворяющее начальному условию у(х₀)=у₀. Изобразите график решения.

Конкретные варианты задания № 1 находятся в конце данных методических указаний.

Порядок выполнения задания №1.

1. Установите автоматический режим вычислений .

2. Запишите правую часть уравнения в виде .

3. Определите подынтегральные функции Х(х) и .

4. Вычислите символьно интегралы с переменными верхними пределами.

5. Запишите уравнение , задающее неявно y(x) как функцию х и решите его символьно относительно переменной y.

6. Определите решение как функцию переменной х.

7. Постройте график найденного решения.

Пример выполнения задания №1.

Решите следующую задачу Коши: . Изобразить график решения.

Разделив переменные получим

.

Далее выполняем пункт 3. Чтобы выполнить пункт 4 , то есть найти явное выражение для решения, запишите в рабочем документе разность вычисленных при интегрировании функций, выделите рамкой переменную y и щелкните по строке Solve в пункте Variable меню Symbolics .

Фрагмент рабочего документа Маthcad с соответствующими вычислениями и графиком приведен ниже.

Указание. Для того, чтобы вычислить символьно интегралы с переменными верхними пределами интегрирования , щелкните по кнопке

в панели , введите в помеченных позициях пределы интегрирования , подынтегральную функцию и переменную интегрирования, выделите интеграл рамкой, щелкните по кнопке в панели и затем—в рабочем документе вне выделяющей рамки.. В приведенном примере уравнение имеет два решения . Выбираем второе из них , поскольку именно для него y(o)=1>0. Для того, чтобы построить график найденного решения, щелкните по кнопке и введите в помеченных позициях аргумент х и имя функции переменной х.