Министерство образования и науки Российской Федерации

Федеральное государственное бюджетное образовательное учреждение

высшего профессионального образования

Московский государственный технологический университет "СТАНКИН"

Егорьевский технологический институт (филиал)

Графический метод решения задач линейного программирования

Методические указания

к выполнению лабораторной работы

По дисциплине

Экономико-математические методы и модели

Ети. ЭмМиМ. 01

Егорьевск 2012

Составитель: кандидат физ.-мат. наук, доцент Т.В. Бармакова

Данные указания предназначены для студентов, обучающихся по специальности 080502 «Экономика и управление на предприятиях (в машиностроении). В методических указаниях приведено содержание и изложен порядок выполнения лабораторной работы № 1 по теме «Графический метод решения задач линейного программирования».

Методические указания рассмотрены и одобрены кафедрой производственного менеджмента

Протокол № ____________ от_________________

Зав. кафедрой ________________А.Т. Замлелая

Методические указания рассмотрены и одобрены методическим советом института

Протокол № ____________ от_____________________

Председатель совета_______________ А.Д Семенов.

Лабораторная работа № 1

«Графический метод решения задач линейного программирования»

Цель работы: Решать задачи линейного программирования графическим методом; исследовать решения системы алгебраических уравнений прямым и ите­рационным методом. Решать задачи ЛП симплексным (обобщённым) методом.

1. Теоретические сведения.

Графический метод решения задач линейного программирования в его непосредственной форме применяется только в случае двух переменных.

Реальные задачи линейного программирования содержат, как правило, большое число неизвестных. В целом, графическим методом, несмотря на его простоту и наглядность, решить такие задачи невозможно.

Обобщённым методом в этом смысле можно считать симплексный метод, который является универсальным, т.к. позволяет решить практически любую задачу линейного программирования, представленную ниже в виде системы в каноническом виде.

Методы решения систем линейных алгебраических уравнений можно разделить на точные и приближенные.

Метод решения задачи относят к классу точных, если в предположении отсутствия округлений с его помощью можно найти результате конечного числа арифметических и логических операций.

1. Симплексный метод решения задач линейного программирования

Решение линейной системы методом Гаусса

Метод Гаусса - точный метод решения невырожденной системы линейных алгеб­раических уравнений. Этот метод состоит в том, что систему п линейных алгебраических уравнений относительно п неизвестных

приводят последовательным исключением неизвестных к эквивалентной системе с треугольной матрицей.

решение которой находят по рекуррентным формулам

В матричной записи это означает, что сначала (прямой ход метода Гаусса) элементарными операциями над строками (перестановка строк, умножение строки на отличное от нуля число, сложение любой строки матрицы с другой строкой, умноженной на отлич­ное от нуля число) приводят расширенную матрицу системы к ступенчатому виду:

а затем (обратный ход метода Гаусса) эту ступенчатую матрицу преобразуют так, чтобы в первых п столбцах получилась единичная матрица:

В Mathcad прямой и обратный ход метода Гаусса выполняет функция rref(A).

Последний (п+1)й столбец этой матрицы содержит решение системы.

1.2. Пример решения системы трех линейных уравнений относительно трех неизвестных методом Гаусса

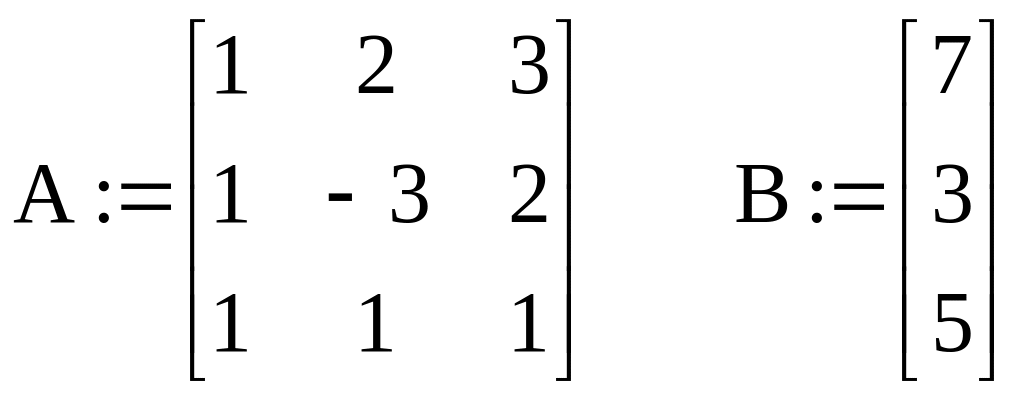
ORIGIN:=1 Ar:=augment(A,b)

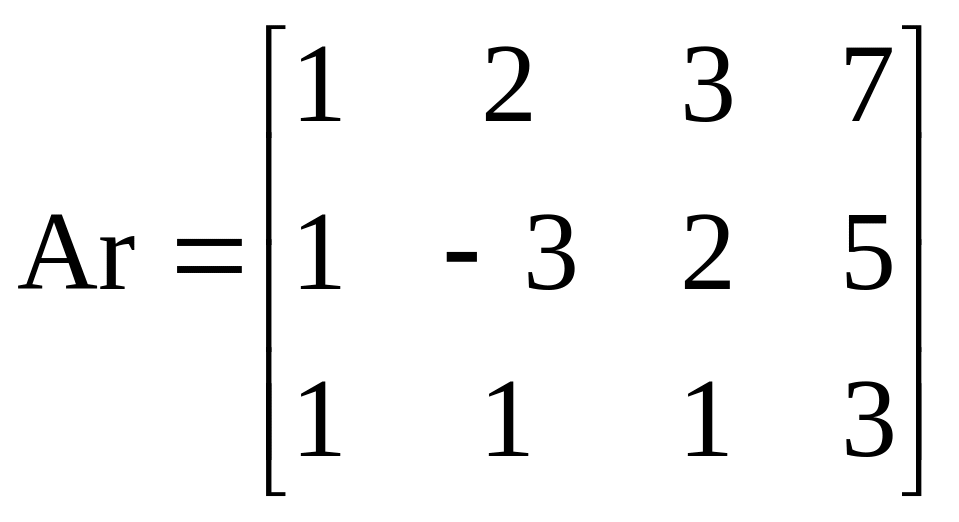
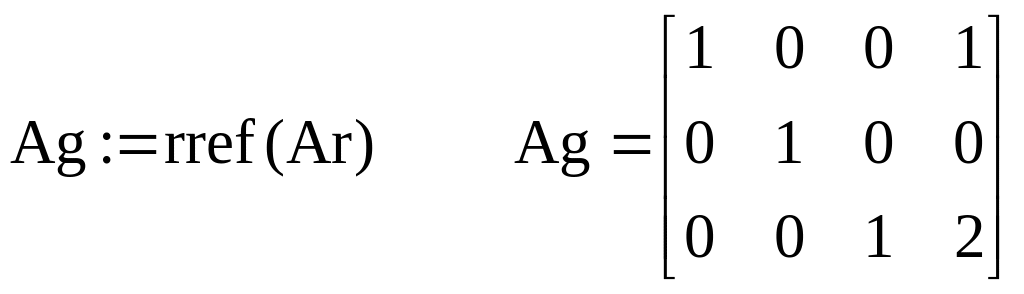
X:=submatrix(Ag,1,3,4,4)

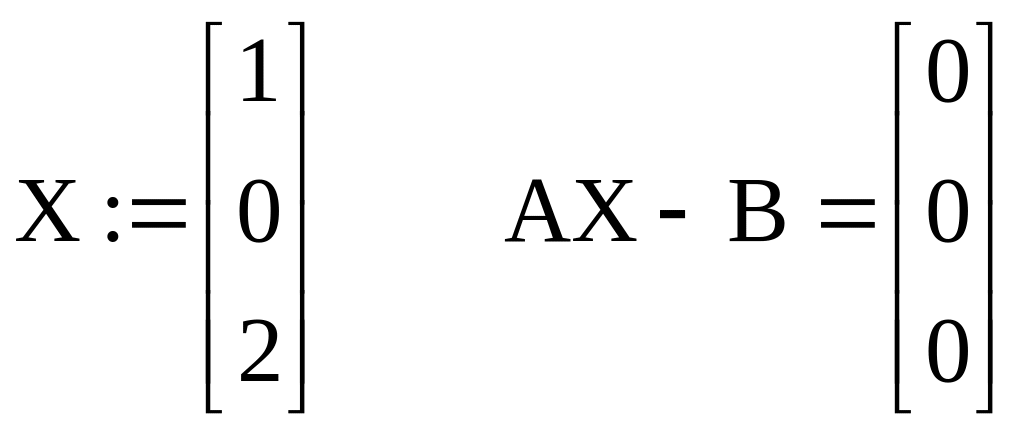
Указание: Для того, чтобы сформировать расширенную матрицу системы, используйте функцию augment (A,b), которая формирует матрицу, добавляя к столбцам матрицы системы А справа столбец правых частей b (Ar). Функция rref (Ar) выполняет элементар­ные операций со строками расширенной матрицы системы Аг - приводит ее к ступенча­тому виду с единичной матрицей в первых столбцах, т.е. выполняет прямой и обратный ход метода Гаусса. Ag - имя результата (ступенчатой матрицы Аг). Функция submatrix (Ag, I, 3, 4, 4), выделяя последний столбец матрицы Ag формирует столбец решения си-темы. Проверка вычисления Ах - b позволяет убедиться в правильности решения.