Лабораторная работа №2

Оптимизация регулятора системы телеуправления при стационарных случайных воздействиях

 ЦЕЛЬ И ЗАДАЧИ РАБОТЫ

Цель исследования – практическое освоение методов оптимального синтеза линейной СТУ при стационарных случайных воздействиях.

Достижение поставленной цели связано с решением следующих задач:

- постановка задачи оптимизации;

- выбор структуры регулятора и корректируемых параметров;

- численная оптимизация параметров регулятора по критерию минимума дисперсии ошибки;

- моделирование скорректированной системы при случайных воздействиях с оценкой точности в среднем;

- анализ устойчивости системы;

- анализ качества регулирования в переходном режиме.

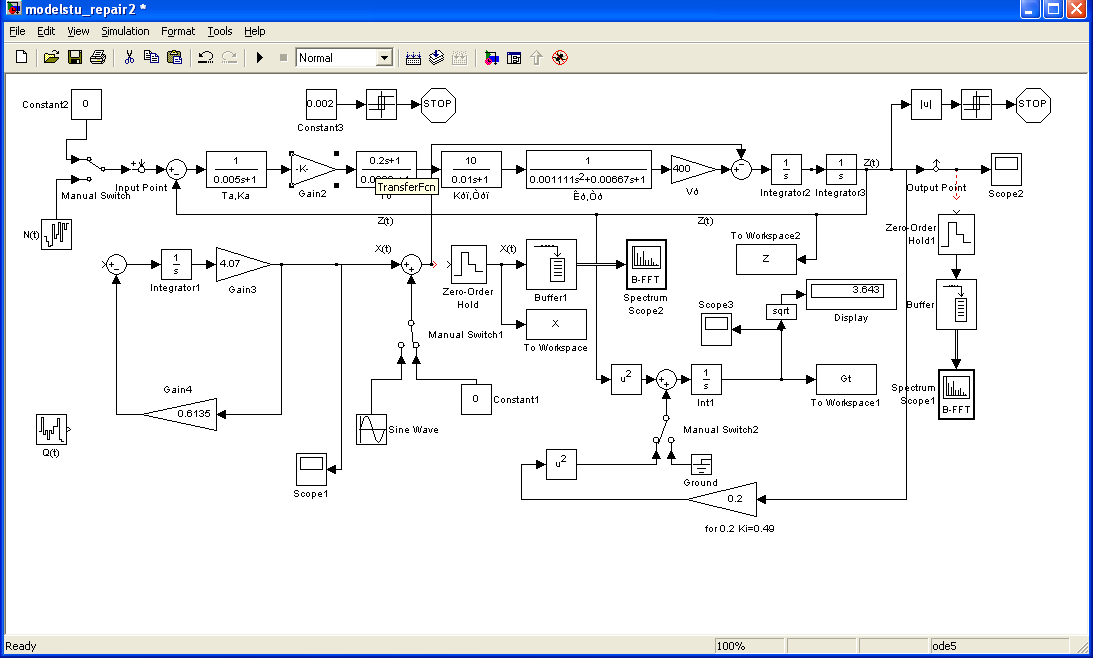
Мы подавали на вход 0,002 и получили средне квадратичное отклонение 3.645.

Проведя оптимизацию мы получили среднее квадратичное отклонение равное 1,822.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1 Какой критерий используется для оценки точности стохастической системы в установившемся режиме?

2 Какую структуру имеет регулятор и какие параметры корректируются?

3 В чем состоит математическая постановка задачи оптимизации СТУ? Какие ограничения должны учитываться?

4 Какие численные методы и стандартные процедуры используются для минимизации?

5 Что такое условная оптимизация СТУ по среднеквадратичному критерию? В чём суть метода штрафных функций? Как он реализуется с помощью Simulink- схемы?

6 Как влияет значение параметра на дисперсию ошибки?

7 Какие показатели динамики должны контролироваться при синтезе?

8 Влияет ли выбор начального приближения на результат оптимизации?

9 Как влияет интенсивность шумовой помехи на результаты оптимизации?

Ответы на вопросы:

1 Критерий точности СТУ

2 В качестве оптимизируемых параметров используются коэффициент передачи системы по разомкнутому контуру, постоянная времени и разнос n дифференцирующего фильтра. ,где – вектор корректируемых параметров регулятора, ; – оптимальное значение вектора. В качестве корректируемого параметра рассмотрим коэффициент передачи Ki разомкнутой системы.

3 Следует задать такое начальное приближение коэффициента, при котором система устойчива. Расчет Ki в диапазоне значений, где система устойчива, сводится к решению задачи однопараметрической минимизации , где Ki^* – оптимальное значение коэффициента.

4 Оптимизация СТУ по одному параметру может производиться с помощью стандартной функции Fminbnd пакета Optimization Toolbox. Эта функция предназначена для скалярной нелинейной минимизации с ограничениями вида x₁< x< x₂. Алгоритм основан на методе золотого сечения и квадратичной (параболической) интерполяции. Функция оптимизации записывается в виде:

Ki = fminbnd(@cget,a,b),

где cget – целевая функция; a и b – границы интервала изменений Ki, который соответствует устойчивой системе.

5 В общем случае задачу оптимизации САУ по критерию минимума среднего значения квадрата ошибки следует ставить как условную, а именно, как задачу оптимизации в условиях ограничений типа неравенств. Последние представляют собой функциональные и параметрические ограничения, которые обусловлены требованиями к показателям устойчивости, колебательности и быстродействия системы, а также требованиями к физической реализуемости параметров регулятора. Метод штрафных функций. В соответствии с этим методом, если в процессе работы алгоритма минимизации будет превышено некоторое граничное значение коэффициента передачи , то к исходной целевой функции прибавляется большая константа. Изображающая точка алгоритма минимизации как бы отскакивает от высоких стен, окружающих ту часть пространства параметров регулятора (в данном случае часть числовой прямой, где ), в которой выполняются функциональные ограничения, в частности, ограничения по запасам устойчивости, показателям колебательности и быстродействия системы.

6 При решении задач условной оптимизации часто используется метод штрафных функций. В соответствии с этим методом, если в процессе работы алгоритма минимизации будет превышено некоторое граничное значение коэффициента передачи , то к исходной целевой функции прибавляется большая константа.

7 Точность, устойчивость, колебательность и быстродействие системы.

8 Для исключения локальных минимумов и для улучшения сходимости алгоритма к глобальному минимуму вводят сетку начальных приближений в пространстве корректируемых параметров. Запуски алгоритма минимизации производятся из узлов этой сетки.

9 Чем интенсивней шумовая помеха, тем дольше будет проводится оптимизация или можно вообще не получить приемлемого решения.