2.3. Погрешности совокупных и совместимых измерений

Структурно процесс этих измерений можно представить в виде рис.2.3.

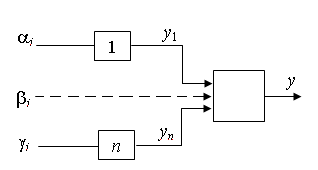
Рис.2.3.Структурное представление процесса измерений

Искомые у₁ до у_п получены в i-м эксперименте в результате прямых и косвенных измерений неэлектрической величины.

Первичные измеряемые величины связаны уравнением вида

.

После подстановки в каждое такое уравнение значений получим

,

где знак равенства имеет чисто условный характер, ибо получение в результате измерений коэффициента, входящего в (4.47) содержит погрешности.

Если в каждое уравнение ввести слагаемое _С, обращающее его в строгое тождество, и называемое невязкой, то задача будет состоять в том, чтобы найти оценки у₁ … у_т при которых сумма квадратов невязок минимальна, т.е. в уравнениях

величины будут удовлетворять условиям

Т.к. то требование минимизации суммы квадратов невязок (0) можно переписать в виде

.

Функция нескольких переменных достигает минимума в точке, где все части произведения ее равны нулю. Поэтому оценки интересующие нас неэлектрической величины находятся из системы уравнений

.

2.4. Общие вопросы определения результирующих погрешностей

Многие аналоговые измерительные приборы являются сложны­ми устройствами, состоящими из нескольких измерительных преоб­разователей. Поэтому для теории и практики важно найти методы определения общей погрешности ППИ по известным погрешностям его преобразователей.

В общем случае это можно сделать, если известна характери­стика преобразования прибора , где – составляющие па­раметры характеристики преобразования ППИ. Естественно, что параметры не остаются постоянными, а изменяются от изменения условий эксплуатации, характера входного сигнала, времени и т. д., а это приводит к появлению погрешности ППИ

(2.6)

В пределах линейной теории точности можно получить оценку суммарной погрешности ППИ, если воспользоваться понятием пол­ного дифференциала функции от нескольких переменных, заменив при этом приращение функции ее дифференциалом. Тогда можно записать

(2.7)

Подставив в это выражение значения аргументов и их прира­щений , получим значение суммарной абсолютной погрешности ППИ.

Очевидно, способ оценки суммарной погрешности будет зависеть от вида выбранной метрики. Так, в равномерной метрике величину предельной суммарной погрешности ППИ определяют из соотноше­ния

(2.8)

В случае применения среднеквадратической (вероятностной) метрики отдельные составляющие суммарной погрешности ППИ рассматриваются как случайные величины или процессы, статисти­ческие характеристики которых известны.

В общем случае для суммирования случайных величин необхо­димо знать совместную функцию распределения этих величин . Плотность распределения суммы этих ве­личин можно записать в таком виде:

(2.9)

Очевидно, эти формулы приводятся одна к другой заменой пе­ременных. На практике обычно и ограничиваются двумерной функ­цией распределения из-за сложности, а иногда и невозможности нахождения многомерных функций распределения погрешностей. Кроме того, всегда можно попарно суммировать составляющие по­грешности ППИ.

В частных случаях, когда случайные величины и незави­симы, двумерная плотность вероятности равна произве­дению плотностей вероятности случайных величин:

(2.10)

и формулы для суммарного закона распределения погрешностей примут такой вид:

(2.11)

Эти формулы обычно называются формулами компози­ции двух законов распределения.

Формулы (2.11) удобны для вычисления численных характери­стик погрешности ППИ только тогда, когда законы заданы одной формулой на всем диапазоне значений аргумента. В противном случае удобнее воспользоваться методами суммиро­вания случайных величин с использованием характеристических функций. Как известно, характеристическую функцию случайной величины находят как преобразование Фурье от закона распределения , если в преобразовании изменить знак перед :

(2.12)

Характеристическую функцию суммы независимых величин определяют как произведение характеристических функций этих величин:

(2.13)

а функцию распределения суммарного закона – обратным преобра­зованием Фурье:

(2.14)

На практике вместо преобразования Фурье для отыскания можно пользоваться таблицами прямого и обратного одностороннего преобразования Лапласа, сдвигая функцию распределения для обеспечения правильного суммирования погрешностей в область положительных значений аргумента.

Суммирование случайных величин значительно упрощается, ес­ли известен вид суммарного закона распределения. Например, используя центральную предельную теорему, можно утверждать, что при суммировании n независимых случайных величин, возмож­ные, значения которых ограничены одним и тем же конечным интер­валом, а сумма дисперсий которых неограниченно возрастает с увеличением числа слагаемых, в пределе получим нормальный закон распределения суммарной погрешности ППИ. Практически это наблюдается уже при количестве слагаемых больше 4–5. В этом случае или тогда, когда знание закона распределения сум­марной погрешности не требуется, числовые характеристики сум­марной погрешности можно найти из известных соотношений

(2.15)

а для коррелированных слагаемых эти характеристики примут вид

(2.16)

где – корреляционный момент величин и .

В этом случае предел допускаемого значения погрешности ППИ можно оценить для любого закона распределения на основании известного из теории вероятностей неравенства Чебышева, а для одномодальных законов – на основании неравенства Кампа – Мейделя.

Поскольку найти взаимную коррелированность погрешностей ППИ сложно, на практике используют различные приближенные, способы нахождения суммарной погрешности прибора по погреш­ностям его преобразователей [33, 37]. Так, например, в [33] все составляющие погрешности ППИ разбиваются на группы взаимно коррелированных между собой погрешностей с коэффициентом корреляции, равным +1 или –1 (знак устанавливается на ос­новании физических соображений о работе ППИ). Внутри этих групп погрешности суммируются алгебраически. Суммарные погрешности групп для определения общей погрешности ППИ сум­мируются геометрически как некоррелированные величины. Для уточнения этой методики предлагается считать, что коэффициент корреляции внутри групп распределен равномерно в пределах от 0 до 1 и от 0 до –1 [37]. Еще более сложна задача синтеза ППИ – по заданной суммарной погрешности ППИ. Общего решения эта задача не имеет. В настоящее время обычно проектировщики ППИ стараются получить минимальные (на данном уровне развития техники и фиксированных затратах) значения погрешностей отдель­ных звеньев ППИ, учитывая ограничения технологического, конст­руктивного и производственного порядков. Далее обычно анализи­руется суммарная погрешность ППИ и корректируются «вклады» отдельных звеньев ППИ в суммарную погрешность прибора.

Для примера, рассмотрим определение погрешности простого ППИ, состоя­щего из двух преобразователей, включенных последовательно и имеющих номинальные характеристики преобразования и . Пусть первый блок имеет си­стематическую приведенную погрешность ±0,5%, а второй ±0,6%. Случайные погрешности преобразователей заданы их законами распределения. У первого преобразователя случайная приведенная погрешность распределена равномерно:

(2.17)

а у второго – по закону Симпсона:

(2.18)

Случайные погрешности преобразователей не коррелированы. Тогда предель­ное значение систематической погрешности ППИ

(2.19)

Суммарное значение случайной погрешности можно определить, найдя закон распределения суммарной погрешности. Это можно сделать, используя преобра­зование Лапласа или характеристические функции.

Изображение закона распределения первого преобразователя имеет вид

(2.20)

а второго –

(2.21)

причем при написании изображений была использована теорема о смещении в вещественной области.

Поскольку погрешности преобразователей некоррелированы, изображение закона распределения суммарной погрешности ППИ запишем в виде

(2.22)

По таблицам или теореме разложения находим оригинал:

(2.22)

и на основании последнего запишем закон распределения суммарной погрешности

(2.23)

Из закона нетрудно найти и числовые характеристики случайной составляющей приведенной погрешности ППИ: .

С вероятностью единица можно найти предельную погрешность такого ППИ:

Задача определения расчетным путем значения результирующей погрешности по известным значениям ряда ее составляющих, называемая обычно задачей суммирования погрешностей, возникает во многих случаях практики. Так, для определения погрешности отдельного измерительного преобразователя необходимо найти результат суммарного действия отдельных составляющих его погрешности. Определение погрешности прибора или канала информационно-измерительной системы (ИИС) также сводится к определению суммарного действия погрешностей всех его преобразователей. Таким образом, задача суммирования погрешностей – это одна из основных задач как при проектировании средств измерений, так и при постановке и проведении измерений [10].

Трудность проведения такого суммирования заключается в том, что все составляющие погрешности в общем случае должны рассматриваться как случайные величины, принимающие в каждой частной реализации самые разнообразные значения. С точки зрения теории вероятностей они могут быть описаны своими законами распределения, а их совместное действие – соответствующим многомерным законом распределения. В такой постановке эта задача практически не разрешима уже для 3-4 составляющих (не говоря уже о 30-40 составляющих), так как операция с такими многомерными законами непреодолимо сложны. Поэтому задача состоит в том, чтобы подобрать для характеристики составляющих такие числовые оценки (например, среднеквадратическое значение, контрэксцесс¹, энтропийный коэффициент и т. д.), оперируя с которыми, можно было бы найти соответствующие числовые оценки результирующей погрешности без определения многомерных или результирующих одномерных законов распределения рассматриваемых случайных величин.

При этом необходимо учитывать следующее:

а) числовые характеристики законов распределения составляющих могут не оставаться постоянными при изменении измеряемой величины, т. е. могут изменяться в диапазоне ее изменения;

б) отдельные составляющие погрешности могут быть коррелированны между собой;

в) при суммировании случайных величин законы их распределения резко деформируются.

Первое из этих обстоятельств требует разделения рассматриваемых составляющих на аддитивные и мультипликативные, суммирование которых производится раздельно для определения соответственно аддитивной и мультипликативной составляющих результирующей погрешности.

Второе обстоятельство, т. е. возможность взаимных корреляционных связей составляющих, учитывается путем использования для характеристики суммируемых составляющих погрешности их числовых оценок в виде среднеквадратического значения и коэффициентов взаимной корреляции.

Третье обстоятельство, т. е. деформация формы законов распределения при суммировании случайных величин, не может быть учтено при использовании оценки погрешности в виде ее среднеквадратического значения, так как эта оценка не отражает деформации формы законов распределения. Это может быть сделано путем определения параметров формы образующей композиции нескольких законов распределения.

Дисперсия суммы коррелированных и некоррелированных погрешностей

Согласно теории вероятностей дисперсии суммы двух величин в общем случае [10]

D(x+y)=D(x)+D(y)+2k_xy, (2.24)

где D(x) – дисперсия x; D(y) – дисперсия y; k_xy=ρ σ(x)σ(y) – их взаимный корреляционный момент (ρ – коэффициент корреляции). Отсюда среднеквадратическое значение σ_Σ отклонения суммы этих величин от ее математического ожидания

(2.25)

Если эти величины между собой некоррелированы, то ρ=0 и

Однако если x и y жестко и положительно коррелированы между собой (ρ=+1), т. е. Δy принимает значения, лишь строго пропорциональные Δx, то всякое положительное отклонение +Δx сопровождается также положительным отклонением +Δy и отклонение Δ(x+y) определяется как Δx+Δy. Это формально следует и из формулы для σ_Σ при ρ=+1, ибо

Если же при возрастании x значения y, наоборот, линейно убывают, то ρ=–1 и

(2.26)

Таким образом, оценки жестко коррелированных погрешностей (ρ=1) должны суммироваться не геометрически, а алгебраически с учетом их знаков, т. е. складывается, когда их знаки совпадают, и вычитаются, когда их знаки оказываются противоположными.

Это правило теории вероятностей в совершенно равной степени относится как к чисто случайным погрешностям, так и к систематическим погрешностям, возникающим от случайного изменения влияющих факторов. Так, например, погрешности измерительных преобразователей зависят от изменений температуры окружающей среды и это влияние хорошо воспроизводится от опыта к опыту и поэтому обычно классифицируются как систематические. Однако при суммировании температурных погрешностей ряда преобразователей они могут оказаться как коррелированными, так и некоррелированными между собой и складываться как алгебраически, так и геометрически.

Практические правила определения результирующей погрешности сложных измерительных устройств

1. Для определения значения оценки результирующей погрешности всего измерительного устройства должны учитываться взаимные корреляционные связи различных составляющих погрешности отдельных преобразователей, поэтому исходными данными для более точного расчета должны служить значения соответствующих оценок именно отдельных составляющих, а не значение оценки суммарных погрешностей преобразователей.

Эти составляющие, прежде всего, разделяются на аддитивные и мультипликативные для их последующего раздельного суммирования.

2. Так как суммировать с учетом корреляционных связей можно лишь среднеквадратические значения составляющих, то для каждой составляющей должны быть по исходным данным найдены ее среднеквадратические значения.

3. Далее должны быть выделены группы сильно коррелированных между собой составляющих погрешности и внутри этих групп произведено алгебраическое суммирование. К ним, как правило, относят погрешности, вызванные одной общей причиной (общий источник питания, примерно одинаковые изменения температуры и т. д.), когда тесные корреляционные связи определяются логически, и для них принимают ρ равным +1 или –1. Погрешности же, между которыми такие взаимосвязи не обнаруживаются, относят к некоррелированным и для них принимают ρ=0.

4. После того как все группы сильно коррелированных погрешностей выделены и внутри их произведено алгебраическое суммирование, суммарные по группам и оставшиеся вне группы погрешности можно считать уже некоррелированными и складывать по правилу σ_Σ²=Σ σ_i².

Таким образом, находятся лишь среднеквадратические значения аддитивной и мультипликативной составляющих результирующей погрешности, которые не учитывают деформации законов распределения при образовании композиций, и остаются неизвестными параметры формы закона распределения результирующей погрешности.