2. Методы оценки погрешностей
2.1.Анализ и оценка погрешностей прямых измерений (по гост 8.207-76)
Неисключенная систематическая погрешность результата измерения, как правило, состоит из следующих составляющих:
- неисключенная составляющая погрешности метода измерения;
- неисключенная составляющая погрешности измерительного преобразователя;
- от других источников.
За границы этих неисключенных систематических погрешностей принимают, например, пределы допусков основной и дополнительной погрешностей СИ (ПП), при условии, что случайной составляющей можно пренебречь в силу их малости.
При суммировании этих погрешностей неисключенные систематические погрешности СИ каждого типа рассматриваются как случайные.
Если данные о виде функции распределения этих погрешностей отсутствуют, то закон распределения – равномерный.
Границы доверительной вероятности неисключенной систематической составляющей погрешности (НСП) вычисляются с помощью композиции закона распределения НСП. Для равномерного закона распределения (РЗР) составляющих погрешностей границы этих погрешностей определяются по функции (без учета знака)
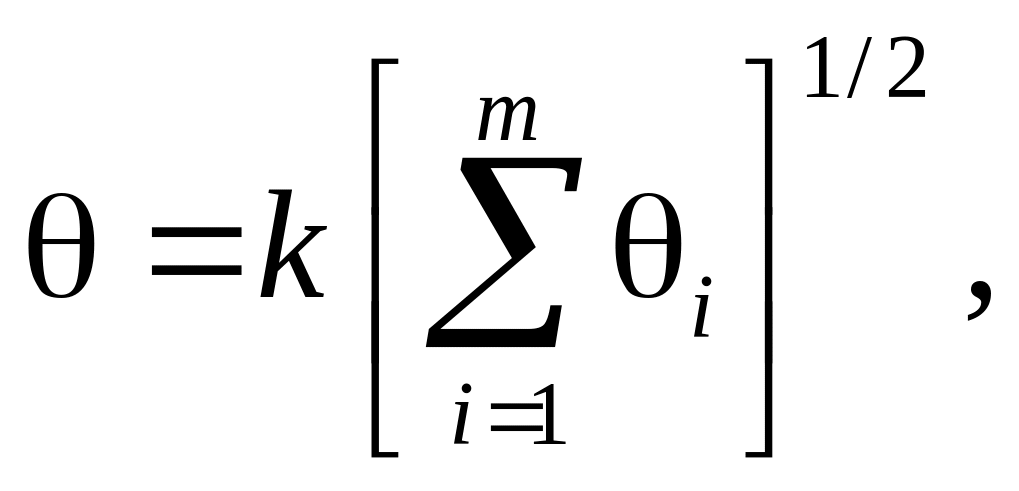
где
- границы доверительного интервала i
– ой неисключенной систематической
погрешности;
k – коэффициент, определяемый принятой доверительной вероятностью и числом суммируемых составляющих m.
Для случая усреднения (с 10% погрешностью усреднения) по m значения k определяются по табл. для m>4
-
0,9
0,95
0,98
0,9
k
0,95
1,1
1,3
1,4
При m<4 определение k сложно.
ГОСТ 8.207-76 Определение границ доверительного интервала см. с.72. (регламентирует процесс определения границ суммарной погрешности ). |
Два случая:
если одна из составляющих больше другой, то меньшей пренебрегают:
-
если
,
где S
– смещенная оценка СКО;
- граница доверительного интервала
неисключенной систематической
погрешности, то неисключенной
систематической погрешностью пренебрегают
по сравнению со случайной и устанавливают,
что граница погрешности результата
измерения =.
-
если
,
то случайной погрешностью по сравнению
с систематической пренебрегают и
устанавливают, что =
.
Доказано, что при выполнении этих неравенств, погрешность, возникающая за счет пренебрежения одной из составляющих не более 15%.
если составляющие соизмеримы, то специальным образом учитывают влияние каждой из них на границу суммарной погрешности.
Если неравенства не выполняются, то границу погрешности результата измерения находят путем построения композиции распределения случайной и неисключенной систематической составляющих погрешностей, рассматриваемых как случайные составляющие.
Если доверительные границы случайных погрешностей найдены, то границы погрешностей результата измерения x (без учета знака) определяется по формуле:
x=kS,
где
– это коэффициент, зависящий от
соотношения случайной и неисключенной
составляющей систематической погрешности;
S
– оценка суммарной СКО результата
измерения.
S=
.
Результат измерения в этом случае запишется
=
=
=
п=
границы неисключенного остатка систематической погрешности
Другие формы представления результата измерения регламентированы ГОСТ 8.011-72.