2. Параметры, используемые в программе «Динамика»

Определяю массу второй ступени ракеты:

кг

Определяю массу первой ступени ракеты:

кг

Определяю длину топливного заряда второй ступени:

м.

Определяю массу обечайки ДУ второй ступени:

кг.

Определяю массу топлива второй ступени:

кг.

Определяю массу в процентах первого блока:

Определяю массу в процентах второго блока:

кг – масса топлива первой ступени;

кг/м³ – плотность боропластика;

Па – модуль упругости боропластика;

м - диаметр Миделя

м – длина первого блока;

м – длина второго блока;

кг – масса головной части;

кг – масса полезной нагрузки;

2.1 Расчет колебаний

Расчет колебаний проводим с помощью программы «Динамика ЛА» для 1-ой моды изгибных, продольных и крутильных колебаний.

Рисунок 4 - Изгибные колебания

Рисунок 5 - Продольные колебания

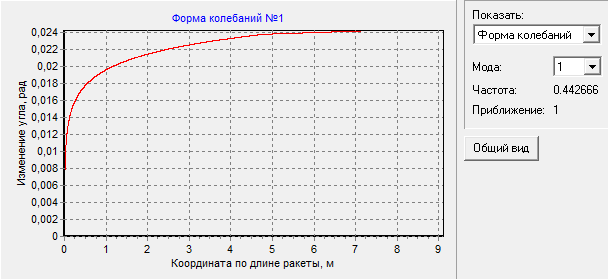
Рисунок 6 - Крутильные колебания

3. Расчет переходного отсека (пОт)

Определяем координату по длине ракеты для расчета как сумму длин 1-ого блока и длины переходного отсека:

Из графиков, полученных в пункте 2, определяем амплитуды колебаний для данной координаты и соответствующие частоты.

Изгибные колебания:

продольные колебания:

крутильные колебания:

3.1 Сжимающая сила:

3.2 Изгибающий момент:

Находим ускорение изгиба:

Плечо приложения момента определяем выражением:

Определяем величину изгибающего момента:

3.3 Крутящий момент:

Угол закручивания . Находим ускорение вращения:

Найдем момент инерции для однородного цилиндра:

Определяем величину крутящего момента:

3.4 Продольная сила:

3.5 Сила, раскрывающая болтовое соединение:

3.6 Определение количества болтов:

Принимаем диаметр болта , материал болта Сталь40.

Определяем несущую способность болта с помощью выражения:

где - допускаемое напряжение для Сталь ЗОХЗМФ (Анурьев, т. 1);

- площадь поперечного принятого болта.

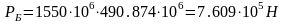
Минимальное количество болтов определяем из соотношения:

_{Окончательно принимаем}

_{3.7 Определение ширины шпангоута:}

Принимаем ширину шпангоута . Проверим контактную поверхность шпангоута на смятие. Материал шпангоута алюминий, для которого допустимое напряжение смятия

Определим площадь контакта:

.

Следовательно, ширина шпангоута удовлетворяет. Окончательно принимаем

3.8 Проверка болтового соединения по допускаемым напряжениям:

Момент инерции сечения болта относительно его центра:

Момент инерции сечения болта относительно оси ЛА:

где

Тогда

_{Полярный момент сопротивления всех болтов относительно оси ЛА:}

Определяем напряжения среза:

Напряжения от растягивающей силы:

Эквивалентные напряжения в болтах составят:

Следовательно, данное болтовое соединение удовлетворяет условиям нераскрытия стыка и условиям прочности болтов.

4. Расчет фермы

4.1 Геометрические параметры фермы

Высота фермы:

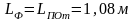
Принимаем количество стержней . Определим длину основания треугольника фермы:

Угол между смежными стержнями:

Длина стержня определяется выражением:

Для стержней фермы принимаем материал алюминий с допускаемым напряжением

Усилие, возникающее в каждом стержне фермы:

Принимаем следующие геометрические размеры стержня:

	- наружный диаметр стержня
	- внутренний диаметр стержня

4.2 Напряжения от усилия сжатия

4.3 Напряжения от крутящего момента

4.4 Эквивалентные напряжения в стержнях фермы

4.5 Проверка на устойчивость

Определяем гибкость стержня:

где

- коэффициент приведенной длины;

- радиус инерции сечения.

Радиус инерции сечения определяем из выражения:

где

- момент инерции сечения при изгибе;

- площадь сечения стержня

Имеем:

Т.к. , то устойчивость определяется из условия , где для алюминия, для алюминия.

Получаем:

удовлетворяются.

Следовательно, условия устойчивости удовлетворяются.