2.3.2 Анализ устойчивости сау с использованием частотного критерия

В качестве частотного критерия устойчивости задан критерий Найквиста. Для анализа САУ необходимо использовать передаточную функцию системы в разомкнутом состоянии.

Для начала мы создали LTI-объект с именем w, в командном режиме среды MATLAB:

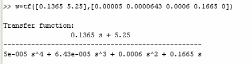
После чего определила нули функции:

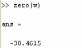
Все «нули» данной передаточной функции отрицательны, следовательно САУ в разомкнутом состоянии устойчива.

Для того, чтобы замкнутая система была устойчива необходимо и достаточно, чтобы амплитудно-фазовая характеристика разомкнутой системы не охватывала точку (-1, 0).

>> nyquist(w)

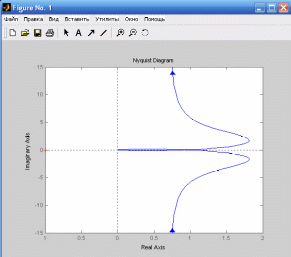
Рисунок 12. Годограф Найквиста.

Годограф не охватывает точку (-1, j0). Следовательно, система устойчива.

2.4 Исследование точности системы.

2.4.1 Анализ влияния коэффициента усиления разомкнутой сау на устойчивость.

Чтобы определить границу устойчивости системы воспользуемся инструментом GUI-интерфейс SISO-Design Tool из пакета прикладных программ Control System Toolbox

>> w=tf([0.1365 5.25],[0.00005 0.0000643 0.0006 0.1665 0])

Transfer function:

0.1365 s + 5.25

--------------------------------------------------

5e-005 s^4 + 6.43e-005 s^3 + 0.0006 s^2 + 0.1665 s

>> p=zpk('p');w=(25*0.21*(0.026*p+1))/(0.25*p*[0.02*0.01*p^3+0.02*p^2*(0.11*0.026+0.01)+(0.11+0.02)+0.02*p*(0.11+0.01)])

Zero/pole/gain:

2730 (p+38.46)

-----------------------------------

p (p+8.628) (p^2 - 7.342p + 75.34)

На основе нашего zpk объекта вызовем SISO-Design Tool командой Sisotool(w)

>> sisotool(w)

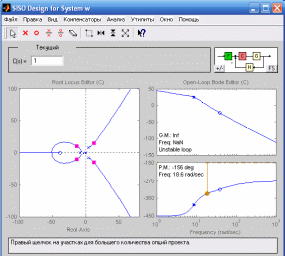
Рисунок 13. Годограф Михайлова.

Передвинем красным курсором по годографу до пересечения с мнимой осью, и определим коэффициент усиления, при котором система находится на границе устойчивости:

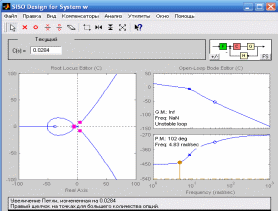
Рисунок 14. Пересечение с мнимой осью.

В результате мы нашли коэффициент усиления, при котором наша система находится на границе устойчивости.

В нашем случае он равен 0,0284.

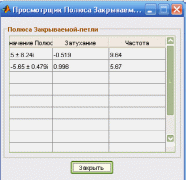
Рисунок 15. Значения полюсов.

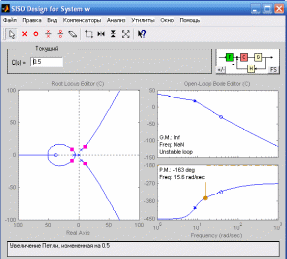
Рисунок 16. Пересечение с мнимой осью.

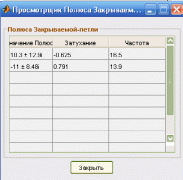
Рисунок 17. Значения полюсов.

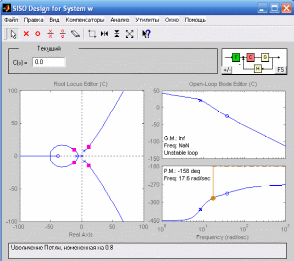
Рисунок 18. Пересечение с мнимой осью.

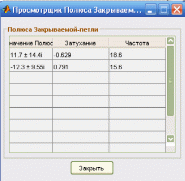
Рисунок 19. Значения полюсов.

На основе использования метода корневого годографа мы получили области значений коэффициента усиления, в которых система автоматического управления является устойчивой.

2.4.2 Определение запасов устойчивости.

Изменение параметров (в частности увеличение коэффициентов усиления и запаздываний) в системах автоматического регулирования может вызвать неустойчивость. Поэтому при проектировании систем регулирования стремятся обеспечить их устойчивость с некоторой гарантией, так что бы изменение параметров в некоторых пределах не могло привести к неустойчивости. Для этой цели используются понятия запасов устойчивости систем. Различают запас устойчивости по амплитуде (модулю) и по фазе. Запасы устойчивости наиболее удобно определять используя логарифмические частотные характеристики.

Найти их можно c помощью команды bode(w)

>> bode(w)

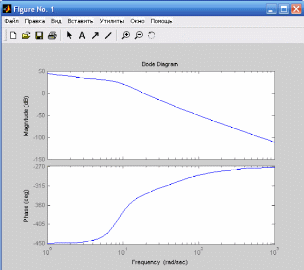
Рисунок 20. Диаграмма Боде

Чтобы построить переходную характеристику воспользуемся командой step(w).Результат ее выполнения приведен на рисунке ниже.

>> step(w)

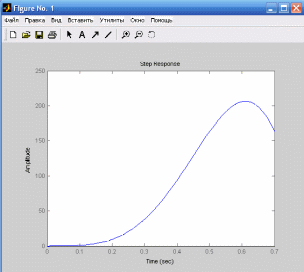
Рисунок 21. Переходная характеристика.