2.2 Синтез системы и определение передаточных функций

2.2.1 Преобразование структурной схемы.

Преобразуем структурную схему (рисунок 4) к стандартному виду, когда все звенья сосредоточены в прямом канале системы, внутренние обратные связи отсутствуют, возмущающее воздействие приложено к выходу системы, а главная обратная связь является единичной.

Используя правило последовательного соединения элементов заменим регулятор тока и тиристорный преобразователь эквивалентным звеном:

(2.1)

Рисунок 5. Преобразованная функциональная схема.

Затем перенесем сумматор и получим звено с обратной связью:

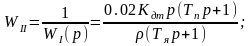
(2.2)

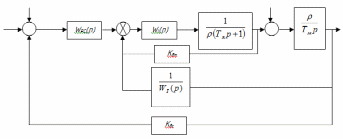
Рисунок 6. Стандартный вид.

Используя правило обратной связи преобразуем схему следующим образом:

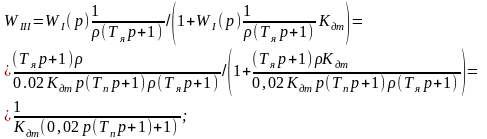
(2.3)

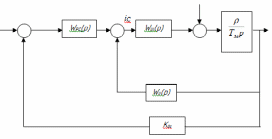
Рисунок 7. Преобразованная схема.

Затем перенесем сумматор и получим следующую схему:

Рисунок 8. Схема с перенесенным сумматором.

Затем опять воспользовавшись правилом обратной связи:

(

(2.4)

Рисунок 9. Конечный вид.

Перенеся узел суммирования на выход системы, окончательно получим схему, по которой можно непосредственно записать все требуемые передаточные функции:

Рисунок 10. Итоговая Схема.

2.2.2 Синтез системы.

Синтез системы автоматического управления является основной стадией проектирования, сущность которой заключается в таком выборе структуры системы, ее параметров и технической реализации, при котором обеспечиваются требуемые показатели качества регулирования.

В нашем случае корректирующим устройством является усилительное звеном К_РС. Коэффициент усиления этого звена равен порядковому номеру студента:

W_РС= К_РС

К_РС=26

2.2.3 Определение передаточных функций.

Упростим значение элемента W_IV:

(2.5)

На основе структурной схемы САУ составим следующие передаточные функции:

Передаточная функция разомкнутой системы

(2.6)

Передаточная функция замкнутой системы по управлению:

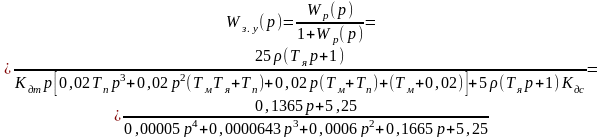
(2.7)

Передаточная функция замкнутой системы по возмущению:

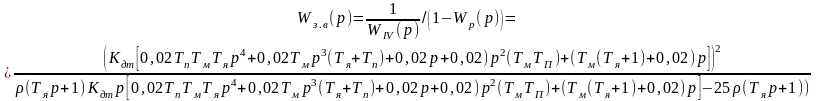
(2.8)

Передаточная функция по ошибке от управления:

(2.9)

2.3 Исследование устойчивости и качества динамических режимов системы.

2.3.1 Анализ устойчивости САУ с использованием частотного критерия.

В качестве алгебраического критерия устойчивости используем критерий Гурвица. Для определения устойчивости по данному критерию необходимо найти характеристический полином замкнутой системы.

Передаточная функция по управляющему воздействию:

(2.10)

Из этого следует характеристический полином:

Так у нас получилось уравнение 4-го порядка, то для того, чтобы САУ была устойчива, необходима и достаточна положительность всех коэффициентов матрицы Гурвица , а также положительное значение определителя 3-го порядка.

0,0000643	0,1665	0	0
0,00005	0,0006	5,25	0
0	0,0000643	0,1665	0
0	0,00005	0,0006	5,25

Рисунок 11.

Из данной матрицы следует:

Можно сделать вывод о том, что САУ не устойчива (определитель 3-го порядка отрицателен).