§ 1.2. Об устойчивости управляющих поверхностей

Исследования напряженно-деформированного cостояния многошарнирного оперения [2] показали, что руль современного самолета при отклонении получает дополнительную нагрузку в своей плоскости, т.к. он вынужден поворачиваться относительно искривленной внешними силами оси шарниров. При этом руль изгибается и в плоскости своей наибольшей жесткости. Нагрузка в срединной плоскости, вызывающая этот изгиб и передающаяся через кронштейны навески, определяется кривизной стабилизатора и углом отклонения руля и достигает больших величин при эксплуатационных и, тем более, при расчетных значениях последних. Это наводит на мысль, что руль, как стержень, имеющий , от действия сил в срединной плоскости может потерять устойчивость, чем-то напоминающую устойчивость плоской формы изгиба балки [1]. Попытаемся выяснить возможность появления такой потери устойчивости в конструкциях оперений современных самолетов [3].

Пусть под действием изгибающего момента внешней нагрузки оперение изогнется. Если предположить, что лобовая жесткость и жесткость на кручение стабилизатора велики, то кривизна его в вертикальной плоскости равна 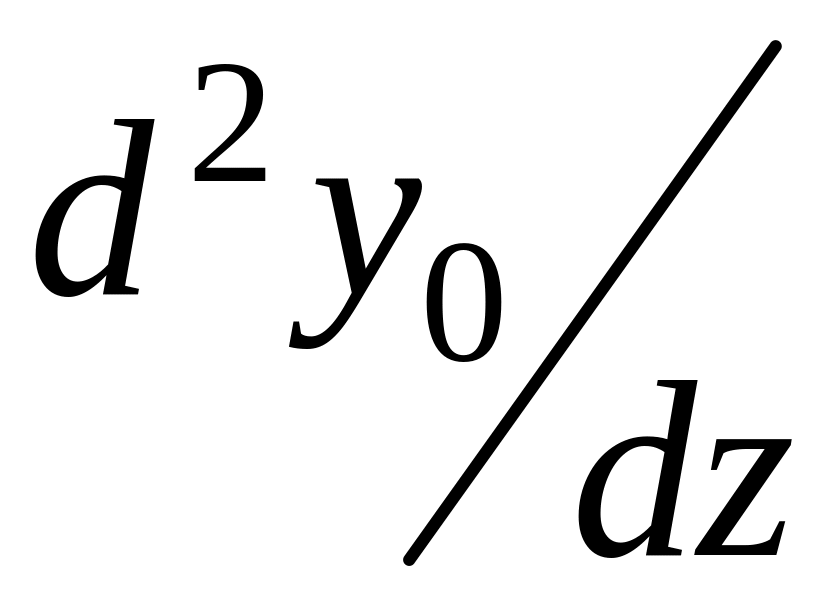(рис. 1.2.1). Предположим далее, что кривизна оси шарниров также равна  ,  а их ось совпадает с центром тяжести сечений руля.

Согласно [1] и рис. 1.2.1.б можем записать кривизну руля в плоскостях xz и yz :

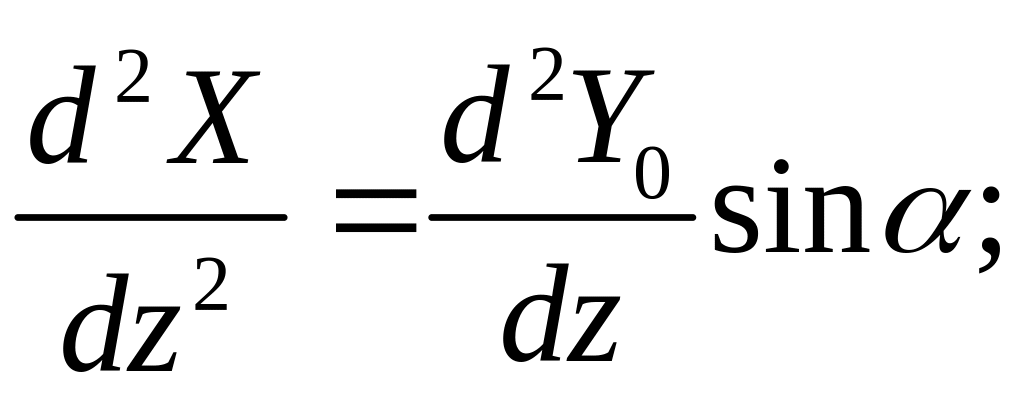
(1.2.1)

а также кривизны и относительный угол закручивания в осях , связанных с сечением руля, которое закрутится на угол  . Для записи последних используем таблицу косинусов С.П. Тимошенко [1], полученную для правой системы координат (рис. 1.2.1,в) .

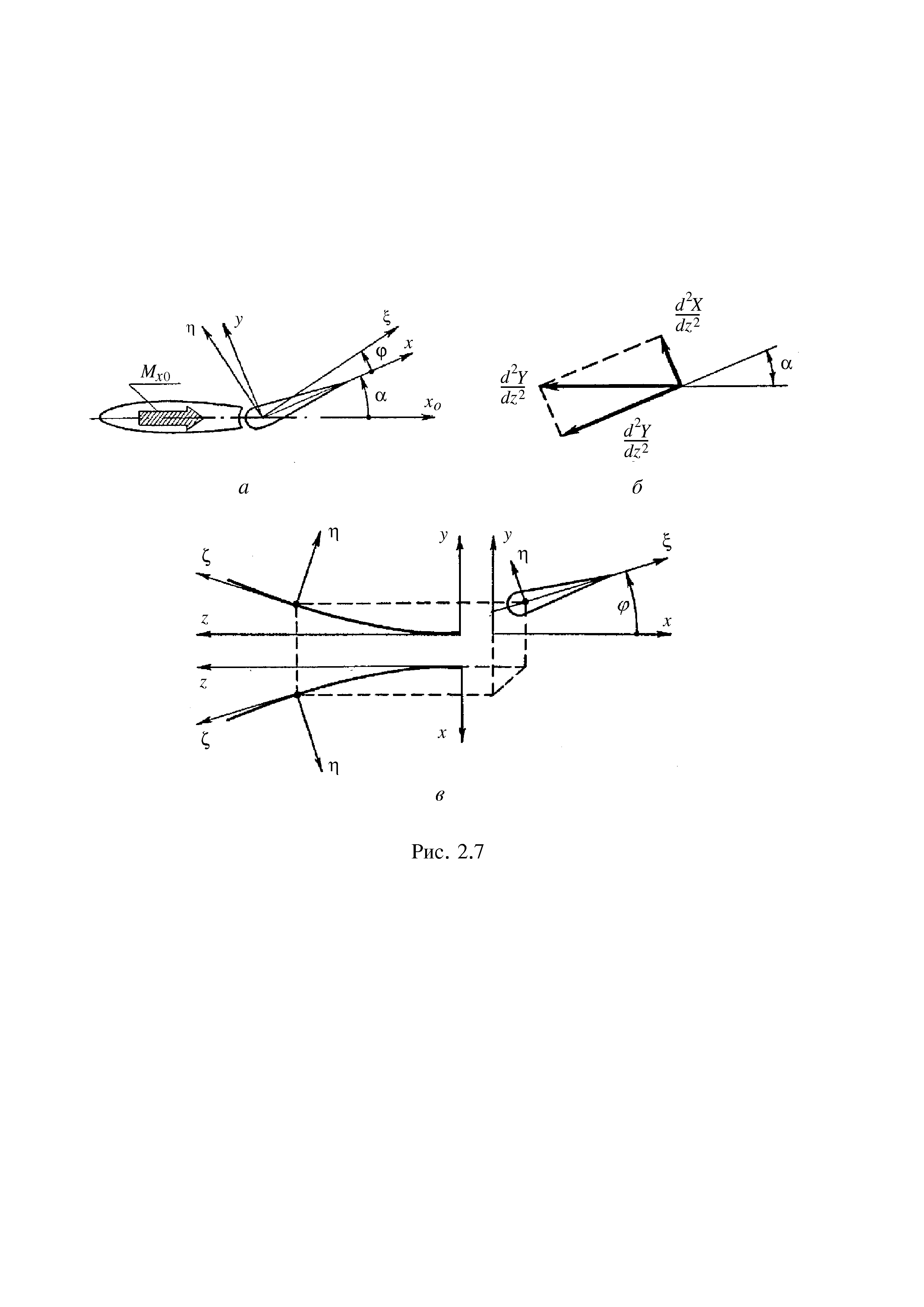
Рис. 1.2.1

Пренебрегая членами, которые С.П. Тимошенко считает малыми, получим:

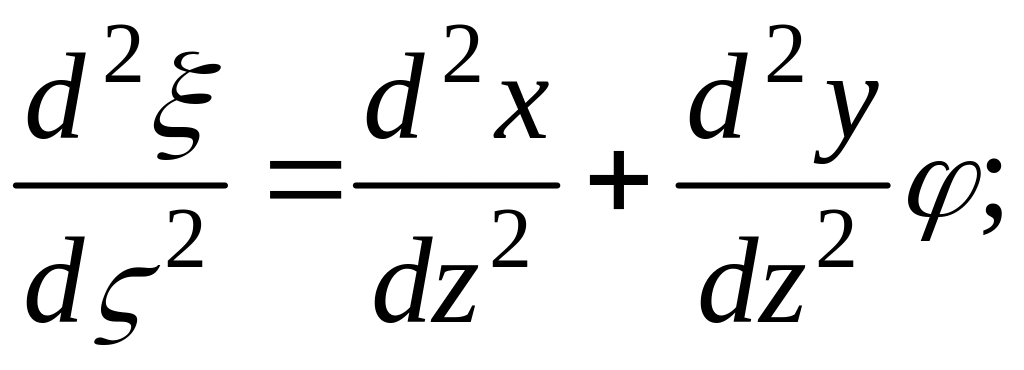
^(1.2.2)

Далее, используя зависимости Кирхгофа - Клебша

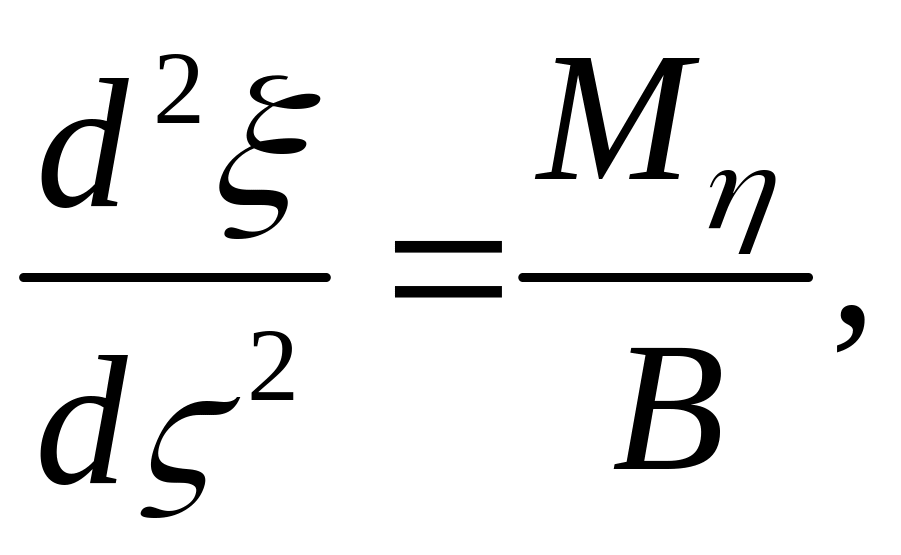
(1.2.3)

где A = , В = и С = , - соответственно минимальная и максимальная жесткости изгиба и жесткость кручения сечения руля, получим моменты внутренних сил относительно осей   в произвольном сечении :

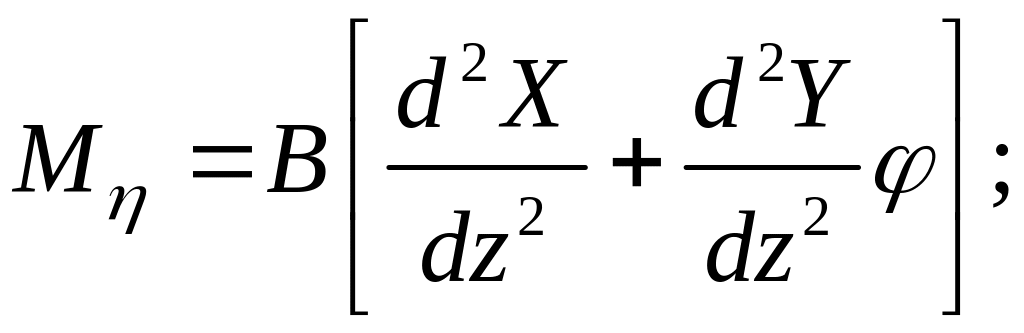
^(1.2.4)

С другой стороны, можно записать соответствующие моменты внешних сил через ту же таблицу косинусов:

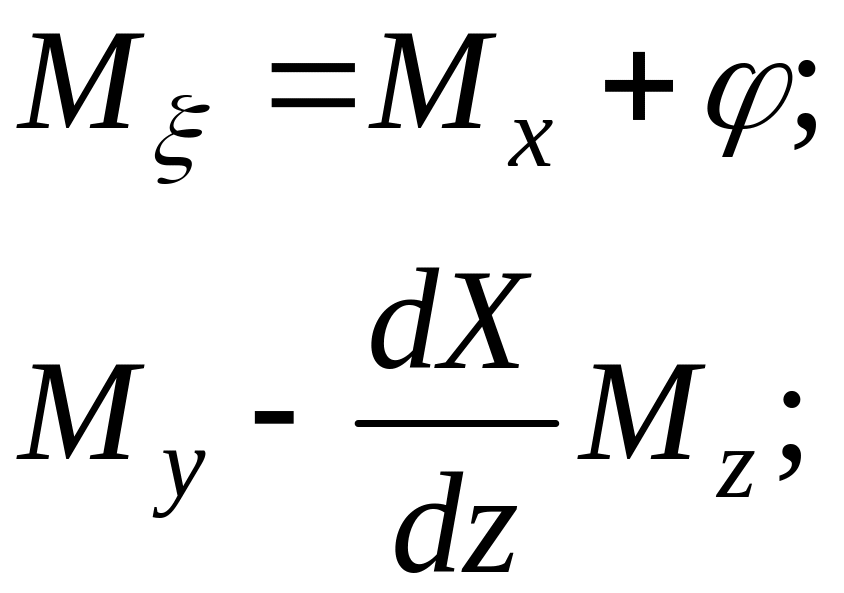
^(1.2.5)

Если предположить, что

(1.2.6)

где - изгибающий момент всей внешней нагрузки, действующей на стабилизатор и руль;

- суммарная изгибная жесткость системы стабилизатор - руль в вертикальной плоскости, то согласно (1.2.1 )

(1.2.7)

Приравнивая (1.2.4) и (1.2.5), принимая во внимание (1.2.7) и заменяя производную по z штрихом, получим:

(1.2.8)

Продифференцируем третье уравнение (1.2.8) по z, считая жесткостные характеристики, а также постоянными:

(1.2.9)

Выразим X" и Y" из первых двух уравнений (1.2.8) и подставим в (1.2.9):

(1.2.10)

Рассмотрим оперение, у которого загружен только стабилизатор постоянным по длине моментом .

При т.е. при решением уравнения (1.2.10) будет:

где

Если качалка управления расположена в сечении z = 0 , то краевые условия примут вид:

1) z = 0 → = 0 ; 2) z = l → = 0 .

Из первого найдем , из второго

тогда

(1.2.11)

Это выражение превращается в бесконечность, если cos kl = 0, т.е. с увеличением значение увеличивается, асимптотически приближаясь к  вертикальной прямой (рис. 1.2.2,а), соответствующей решению однородного дифференциального уравнения, полученного из (1.2.10). Каждому углу отклонения руля будет соответствовать свое значение :

. (1.2.12)

Рис. 1.2.2

При таком значении произойдет потеря устойчивости оперения от действия сил только в его срединной плоскости. Рассматривая решение лишь однородного уравнения (1.2.10), мы как бы отбрасываем влияние поперечных реакций взаимодействия руля и стабилизатора на критическое значение изгибающего момента.

Рассмотрим возможность появления потери устойчивости оперения при некоторых предельных эксплуатационных напряжениях в поясе лонжерона стабилизатора:

(1.2.13)

Здесь   - предельное напряжение; h - высота лонжерона стабилизатора.

Подставляя (1.2.12) в (1.2.13), получим

(1.2.14)

Рассматривая (1.2.14) как равенство, получим значение критического угла отклонения руля, при котором потеря устойчивости оперения наступает одновременно с появлением предельных напряжений в лонжероне.

Построим зависимость от h / l при различных , в том числе и при напряжении, соответствующем пределу пропорциональности материала. При построении кривых (рис. 1.2.2,б) использованы следующие исходные данные:

B/A = 40, A = C, E = 7,2 × 10⁴ МПа , = 300 МПа ,

= 200 МПа, = 100 МПа .

Расчеты самолета на прочность ведутся на напряжения временного сопротивления материала, поэтому представляет интерес и тот случай, когда потеря устойчивости оперения происходит при нагрузках больше эксплуатационных.

Все кривые асимптотически стремятся к значению Из анализа выражения (1.2.14) видно, что во всех практически интересных случаях подкоренное выражение близко к единице и

Случаи при решении уравнения (1.2.10) рассматривать не будем как менее интересные.

Таким образом, при определенном соотношении жесткостей руля и стабилизатора под действием внешней нагрузки может произойти потеря устойчивости руля, если он отклонен на некоторый угол, который больше критического.

Полученное решение следует рассматривать лишь как введение в вопросы устойчивости оперения. Эксперименты на простейших моделях показывают, что конструкция типа оперения с рулем имеет еще одно равновесное состояние, не смежное с первоначальным, при больших прогибах оперения. Явление перехода от одного равновесного состояния к другому сопровождается щелчком, "прощелкиванием" и получило название – катастрофическое изменение формы оперения. При исследовании этого явления необходимо учитывать конечность прогибов, а значит, решать геометрически нелинейную задачу.