Горизонтальное оперение самолета Як-40.
Эксперимент,
описанный ниже, проведен на серийной
машине Як-40, как дополнение к программе
испытаний. В отличии от многих других
программ, при испытании Як-40 требовалось
провести нагружение стабилизатора до
100% расчетной нагрузки с рулем, отклоненным
вверх на
.
На
кронштейны навески руля, которые не
имеют серьги и поэтому загружены тремя
составляющими реакции
,
и
,
были наклеены тензодатчики по схеме,
изображенной на рис. 1.1.4. Датчики
и
имеют в том же сечении симметрично
расположенные датчики
и
на
нижнем поясе кронштейна. Напряжения в
точках наклейки датчиков
,
,
и
можно записать через значения напряжений
в этих точках, вызываемые отдельными
составляющими реакций
,
,
.
Для кронштейна, имеющего две плоскости симметрии, они примут вид:
(1.1.11)
Здесь
- площадь кронштейна в сечении наклейки
тензодатчиков,
,
-
моменты инерции сечения кронштейна
относительно соответствующих осей.
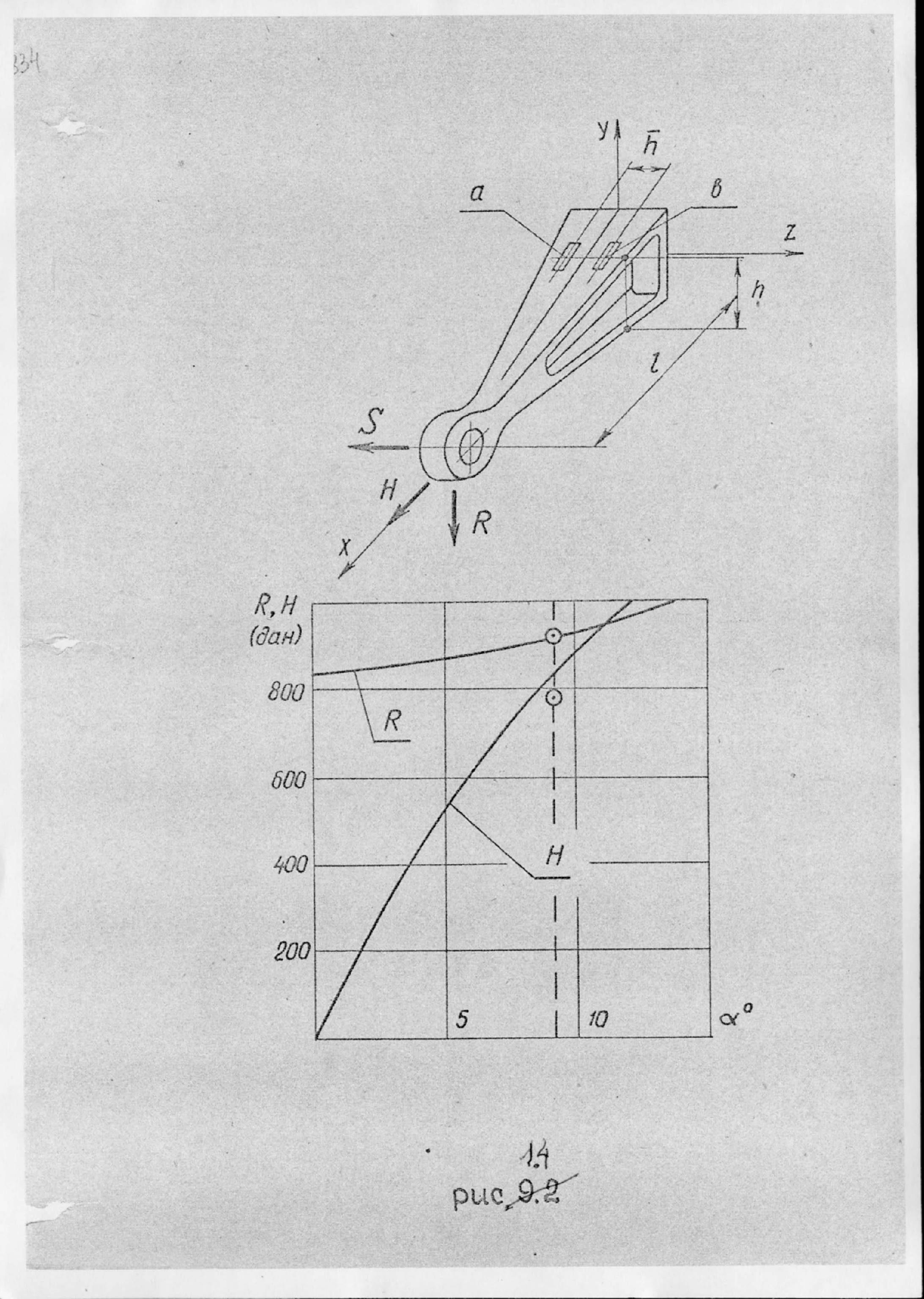
Рис. 1.1.4
Изменяя знаки отдельных уравнений на противоположные и суммируя все четыре уравнения при различных комбинациях знаков, получим
.
Далее по найденным из эксперимента напряжениям , , и можно определить составляющие реакций, действующие на кронштейны:
,
,
.
На
рис. 1.1.4 изображен график изменения
реакций
и
во втором
от заделки стабилизатора кронштейне
навески руля в зависимости от угла
отклонения
.
На график теоретического расчета
нанесены точки результатов эксперимента.
Реакции
и
получены по 1.1.12 при
.
Этот угол отклонения руля соответствует
его равновесному состоянию при 67%
расчетной маневренной нагрузки, при
которой первоначальный угол отклонения
уменьшается до
за счет упругости проводки управления.
Эксперимент подтверждает факт
существования больших составляющих
реакций
в реальных конструкциях, а также
достаточную надежность метода расчета.
Изображенным кружками значениям
=778
дан,
=908
дан соответствует составляющая реакции
в направлении оси шарниров
=20
дан.
Шарнирные моменты.
Момент в качалке управления, или шарнирный момент, по традиционной схеме расчета определяется так:
(1.1.13)
Здесь
составляющая погонной воздушной
нагрузки, направленная по нормали к
плоскости руля;
расстояния от передней кромки сечения
руля до его центра давления и оси
шарниров.
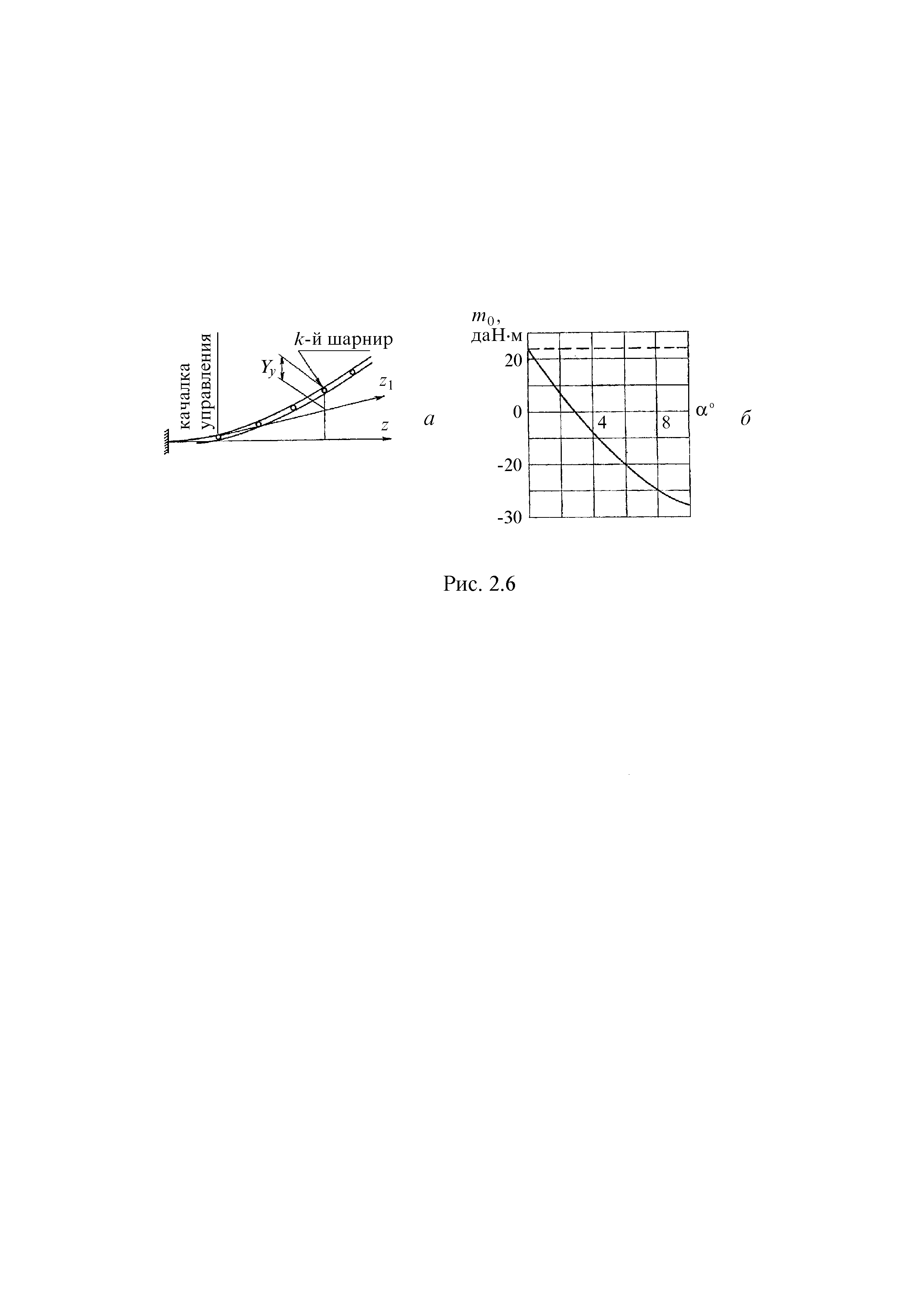
Рис. 1.1.5
Более точное определение шарнирного момента связано с решением геометрически нелинейной задачи, с решением по деформированной расчетной схеме. Действительно, горизонтальные составляющие реакций на перемещениях, связанных с прогибами оси шарниров в вертикальной плоскости, дадут дополнительные моменты относительно оси нулевого шарнира (рис. 1.1.5,а). Если сами являются функциями перемещений оперения, то их произведения на прогибы будут представлять нелинейные зависимости. В первом приближении можно уточнить значение шарнирного момента, зная реакции и прогибы оси шарниров из линейного решения, описанного в данном параграфе.
Полученные
таким образом добавки вносят существенные
коррективы в 
,
но окончательно оценить это можно, лишь
решив задачу в геометрически нелинейной
постановке. На рис. 1.1.5,б
сплошной линией изображено изменение
момента
,
вычисленного относительно оси нулевого
шарнира оперения Ту-104, в зависимости
от угла отклонения руля
.
Напряженно-деформированное состояние
принято известным, определенным по
расчетным нагрузкам в соответствии с
[2]. Искомый момент вычислялся по формуле:
(1.1.14)
первый член которой представляет собой шарнирный момент, вычисленный по недеформированной расчетной схеме (1.1.13), второй - учитывает перемещения точек приложения реакций под действием внешней нагрузки (деформируемость расчетной схемы). Пунктирная линия показывает шарнирный момент, вычисленный по (1.1.13) и не зависящий от . Шарнирный момент с учетом деформаций оперения, изображенный сплошной линией, существенно отличается от момента, определяемого по традиционной схеме.