Совершенствование метода расчета. Лобовые реакции.

Предлагаемый метод расчета многошарнирного оперения с учетом отклонения руля [2] по существу представляет собой метод сравнения перемещений [8], в котором приходится увязывать перемещения руля и стабилизатора не только в вертикальной, но и в горизонтальной плоскости.

Рассматривается оперение, руль которого навешен на (п+2) шарнирах (рис. 1.1.2), где n = 1, 2, 3, ..., и отклонен на угол .

Оперение может иметь переменную по длине жесткость и произвольную внешнюю нагрузку. Решение заключается в определении реакций и в шарнирах навески и строится в следующих предположениях:

1) руль и стабилизатор жестки на кручение;

2) лобовая изгибная жесткость стабилизатора велика;

3) кронштейны навески руля жестки в направлении и и податливы (все, кроме одного) в направлении оси z .

Для решения этой статически неопределимой задачи выбираем основную систему: руль предполагается навешенным только на крайние шарниры. При таком креплении точки i' руля и i стабилизатора под воздействием внешней нагрузки разойдутся (на рис. 1.1.2,б изображена i-я точка).

Рис. 1.1.2

Для выполнения условий их совместности необходимо в каждом шарнире к рулю и стабилизатору приложить усилия: к стабилизатору - и  , к рулю - и (на рис. 1.1.2,в изображены положительные направления векторов сил). Известно, что равнодействующие векторов и  , а также и , и представляют собой равные и противоположно направленные векторы, на основании чего

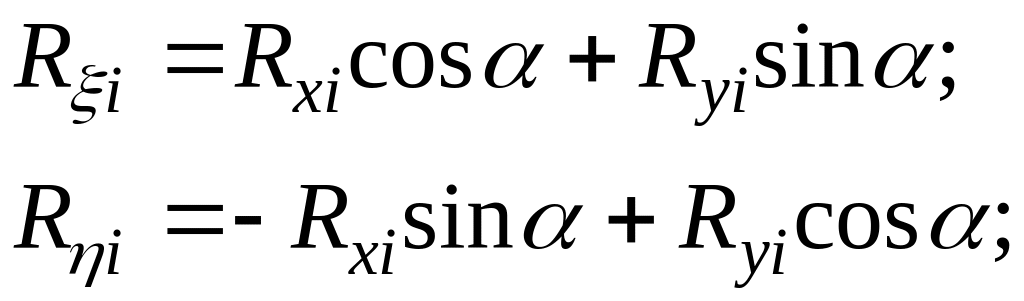(1.1.1)

Под действием этих, пока еще не известных, сил i'-я точка руля и i-я точка стабилизатора должны совместиться. Если предположить, что эти перемещения происходят лишь в плоскости сечения, то для каждой из n точек можно записать по два условия:

(1.1. 2)

Здесь и - перемещение i-й точки стабилизатора в направлениях x и y; и - перемещения i-й точки руля в направлениях x и y.

Условимся вычислять перемещения относительно оси z, считая, что она всегда проходит через точки 0 и n + 1. На основании высказанного предположения о большой жесткости стабилизатора в направлении оси x перемещение = 0 и первое условие (1.1.2) примет вид:

= 0. (1.1.3)

Такое перемещение руля выгодно представить в виде геометрической суммы (рис. 1.1.2,б) перемещений: - в плоскости хорд руля и - по нормали к плоскости хорд, т.е.

Тогда условия (1.1.2) с учетом (1.1.3) запишутся так:

(1.1.4)

Таких условий можно записать 2n для определения 2n неизвестных и .

Не зная пока и , найдем перемещения, входящие в (1.1.4), от единичного загружения. Будем последовательно прикладывать единичную нагрузку во всех шарнирах навески. Приложим ее в k-м шарнире в следующем виде: зададим и , они приложены к рулю и вызывают в i-й точке руля перемещения и . Отыскивать перемещения стабилизатора от нагрузки в направлении осей и неудобно. Лучше отыскивать перемещения в главных центральных осях от нагрузки, приложенной в направлении тех же осей.

Найдем, таким образом:  перемещение в i-м шарнире стабилизатора в направлении оси y от единичной силы, приложенной в k-м шарнире и направленной по оси  y. Аналогичные перемещения руля и стабилизатора в основной системе от внешнего загружения обозначим соответственно через , и тогда полные перемещения можно записать:

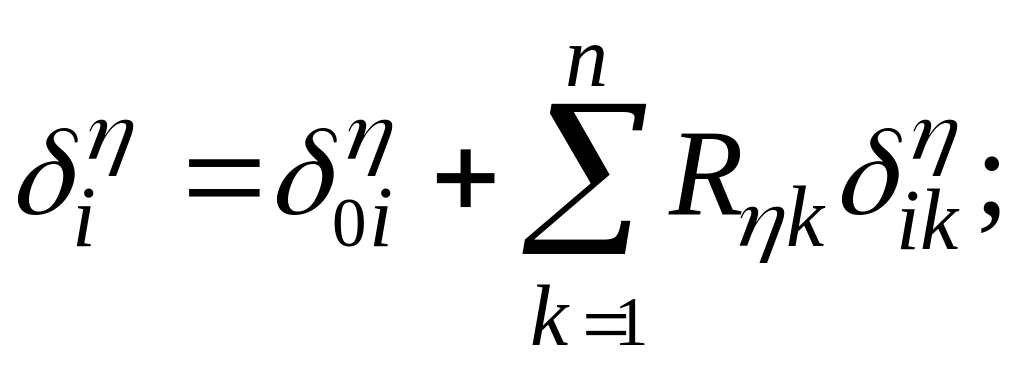(1.1.5)

Условия (1.1.4) выполнятся лишь в том случае, если в (1.1.5) примут истинные значения. Найдем реакции из уравнений (1.1.1) с учетом (1.1.5) и (1.1.1).

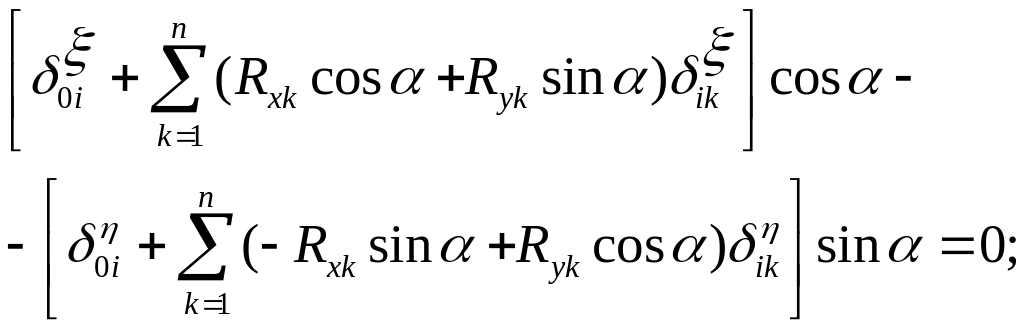
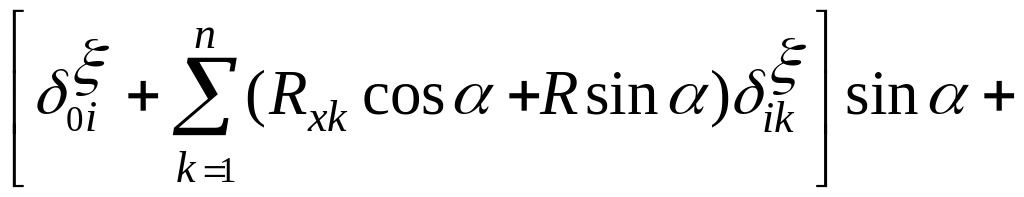(1.1.6)

Преобразуем уравнения (1.1.6) к каноническому виду относительно неизвестных реакций и запишем в виде совместных подсистем:

(1.1.7)

(1.1.8)

коэффициенты которых имеют вид:

(1.1.9)

Здесь , , , .

Выражения (1.1.9) справедливы и при i = k .

Совместное решение систем (1.1.7) и (1.1.8) дает реакции и во всех n промежуточных шарнирах. Реакции в крайних шарнирах определятся так:

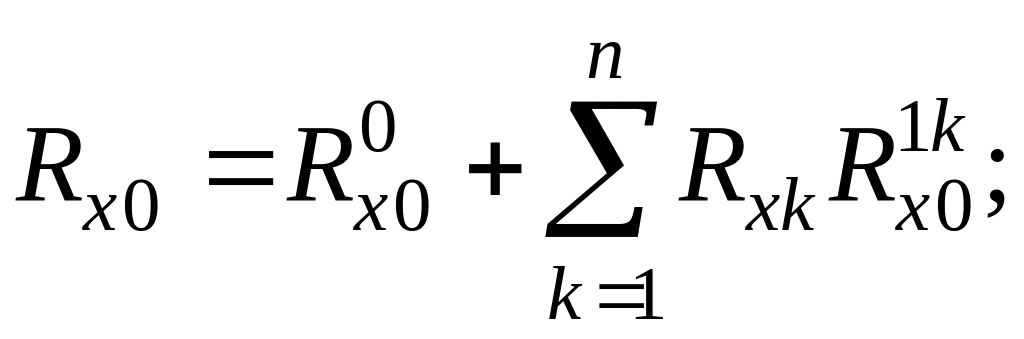
(1.1.10)

^{Здесь и} составляющие полных реакций в k-м шарнире, индекс 0 и n+1 внизу означает номер шарнира, а индексы 0 или 1k вверху определяют соответственно загружение  основное или единичное. Например: составляющая реакции в направлении оси y в (n+1)-м шарнире от основного загружения: составляющая реакции в направлении оси x в нулевом шарнире от единичной силы, приложенной в k-м шарнире.

Достоверность результатов, полученных в §1, подтверждена экспериментально, как на моделях, так и на реальных конструкциях. Приведены результаты эксперимента на модели трехопорного руля, отклоненного на некоторый угол, сечения которого практически не закручиваются в процессе деформации, что дает нам право рассчитывать его по методу [2]. Сравнение с результатами расчета модели, проведенного указанным методом, показывает на достаточную правоверность принятых при описании предложенной расчетной схемы гипотез. Приведены результаты эксперимента горизонтального оперения самолета Як-40, хорошо согласующиеся с расчетом по вышеуказанному методу.

Создана экспериментальная установка, внешний вид которой представлен на фотографии (рис. 1.1.3). Отклоненный руль моделируется трехопорной пластинкой из материала Д-16, длина которой 300 мм, сечение постоянно по длине и равно 4х9х25. Соотношение между максимальной и минимальной жесткостями изгиба пластинки равно 26. Отклоненная на некоторый угол пластинка загружается силой в средней опоре, которая может перемещаться лишь в вертикальной плоскости (на разрезе А-А пластинка изображена в деформированном состоянии). Такая загрузка пластинки соответствует деформированию жесткого на кручение руля, который навешен на стабилизаторе абсолютно жестком в своей плоскости, при этом руль не загружен собственной нагрузкой, а деформируется лишь за счет реакций и , являющихся результатом изгиба стабилизатора.

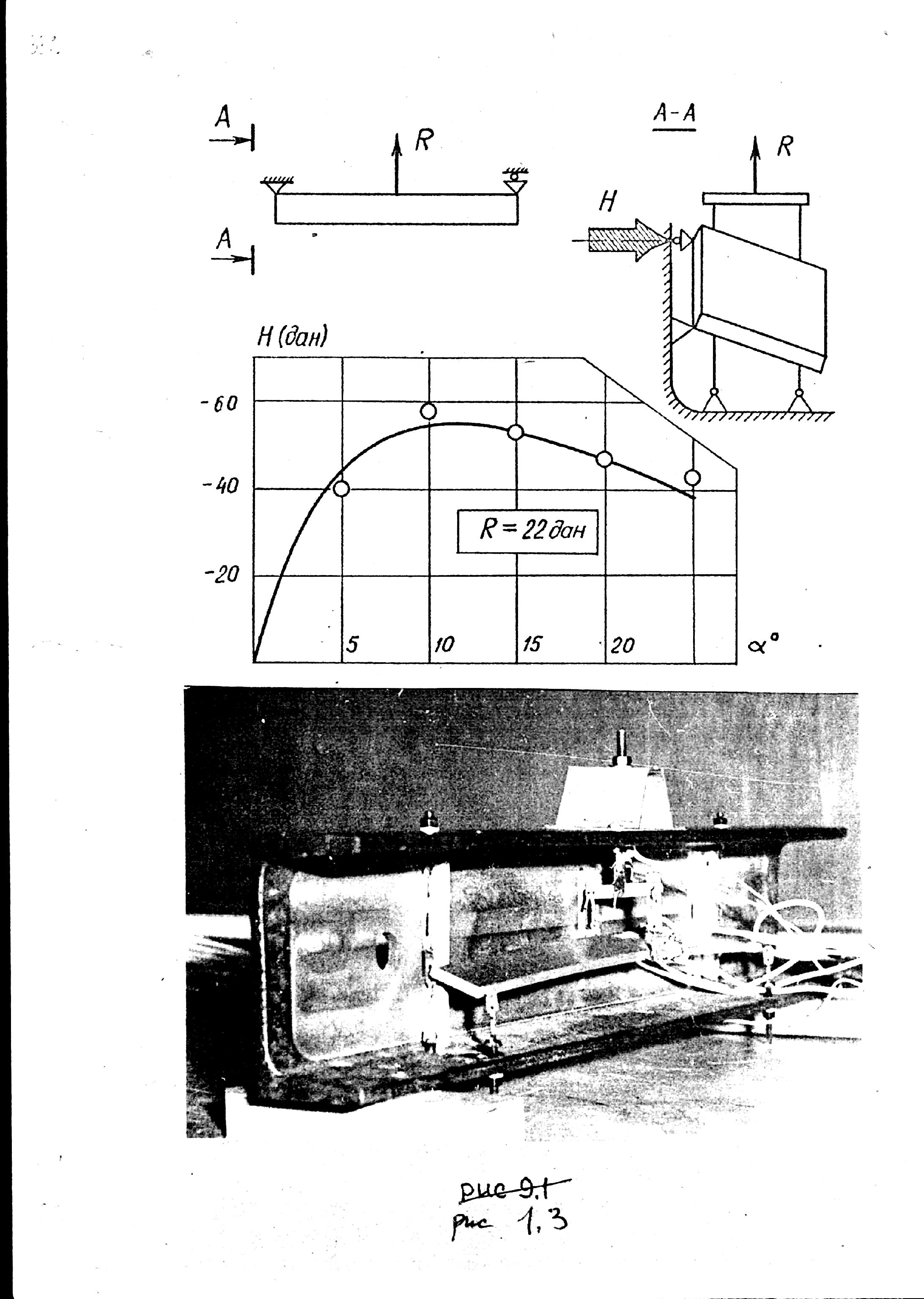
Рис . 1.1.3

Загружение и соответствующая ему в средней (подвижной) опоре осуществлялись тензометрическими тягами. Изменение по при постоянном дан , полученное экспериментально, изображено точками на графике рис. 1.1.3. Сравнение с теоретической кривой говорит о достоверности предложенной расчетной схемы.