§2.3.Колебания катастрофического изменения формы Вводные замечания

Детальное теоретическое и экспериментальное исследование катастрофического изменения в квазистатической постановке  “прощелкивания” на модели трехшарнирной симметричной составной конструкции представлено на рис. 2.2.6. График  ( ) подтверждает выводы о существовании несмежных форм равновесия в составных конструкциях с отклоненными рулями[4]. При увеличении нагрузки конструкция скачком переходит из точки А в точку В - происходит прощелкивание (катастрофа). При разгрузке обратное прощелкивание происходит уже при другой нагрузке скачком из точки С в Д.

На кривых  (р),  (p) (рис. 2.3.1) можно объяснить происходящее в потоке явление. Нагружение крыла, находящегося в равновесном состоянии 0-0 происходит за счет угла атаки крыла ₀ и угла отклонения рулевой поверхности на угол . Аэродинамические нагрузки, определяемые этими углами, приводят к деформированию крыла. Кривая (р) определяет изменение прогиба крыла, (р) - угла закручивания руля. Если ₀ и  таковы, что  и  достигнут точек 1 на соответствующих кривых, то начнется резкий, скачкообразный переход рассматриваемого сечения в точки 2 под действием упругих сил Р и аэродинамических сил P_a. Руль закрутится, угол отклонения руля, влияющий на величину подъемной силы, уменьшится, стремясь к нулю. Аэродинамическая нагрузка, с переходом к точке 2, уменьшится на величину  P₁. Далее, если P₁  P_кр, равное Р_в - Р_н , система остановится в равновесном состоянии на участке 2-3, в точке, соответствующей  P₁. Сечение крыла при этом перейдет из положения 1-1 в положение 2-2. Произойдет катастрофическое изменение формы (прощелкивание).

Если же P₁  P_кр, то система не останется в верхнем положении, а пройдя через точку 3 (положение 3-3), под действием упругих сил Р_у, устремится обратно к точке 4, к своему исходному положению. Восстанавливается форма руля, который увеличивает подъемную силу на величину P₂. Если P₂  P_кр, то произойдет остановка, соответствующая P₂ (обратная катастрофа в область исходного равновесного состояния). Если же P₂  P_кр , то система, переместившись к положению 1, совершит новую катастрофу к точке 2, то есть цикл повторится вновь. Начнутся последовательные переходы, из области одного равновесного состояния в другое и обратно - колебания катастрофического изменения формы крыла.

Теория движения составных стержней

Проблемам исследования движения конструкций, которые по своей расчетной схеме могут быть представлены стержнями, посвящена обширная литература. Это работы по колебаниям стержней в пустоте и в потоке жидкости или газа, колебания собственные и вынужденные, параметрические и аэроупругие и, наконец, линейные и нелинейные.

Свободные колебания, для исследования которых используются линейные дифференциальные уравнения, могут быть разложены по собственным формам и частотам. Проблема разложения собственных колебаний стержня на формы и частоты, начатая ещё Л.Эйлером в настоящее время хорошо разработана и считается классической.

Обращение к линеаризованным решения вынужденно, т. к. они неизмеримо проще линейных. Однако, практически, любое реальное движение упругой конструкции по своей природе нелинейно и линеаризация представляет собой, в той или иной степени, приближение. В каждом отдельном случае очень желательно знать насколько правомерна такая линеаризация.

Рис. 2.3.1

Для построения уравнений движения достаточно в уравнения (2.2.6) ввести инерционные(массовые) нагрузки. Для этого достаточно погонные нагрузки стабилизатора и , погонные нагрузки руля , и моменты , входящие в эти уравнения, считать суммой аэродинамических и инерционных сил, т.е.

, ,

, , (2.3.1)

, .

Аэродинамические нагрузки будем считать зависящими не только от перемещений стабилизатора x⁰ , y⁰ и φ^{0 , перемещений руля x, y и φ (2.2.2), но и от их производных. Запишем их в решении в соответствии с [16], понимая, что лучше было бы для этого использовать метод дискретных вихрей С.М. Белоцерковского. Следует заметить, что в 70-е годы, когда строилась приведенная теория, еще не было соответствующей вычислительной техники, а в последнее время в России предельно ослаб интерес не только к новым теориям, но и к авиационной технике вообще.}

^{Для построения инерционных характеристик в произвольном сечении стержня (рис.2.3.2) закоординируем положение центра масс (ц.м.) в подвижных осях ξη с началом в центре жесткости сечения вектором} .

Перемещения ц.м. связаны с перемещениями ц.ж.

(2.3.2)

и определяют его ускорение (ц.м. руля)

(2.3.3)

Д ля стабилизатора можно записать

Вторые члены этих выражений содержат расстояния между ц.ж. и ц.т., которыми, чаще всего, можно пренебречь в связи с большими перемещениями, свойственными обнаруженному явлению.

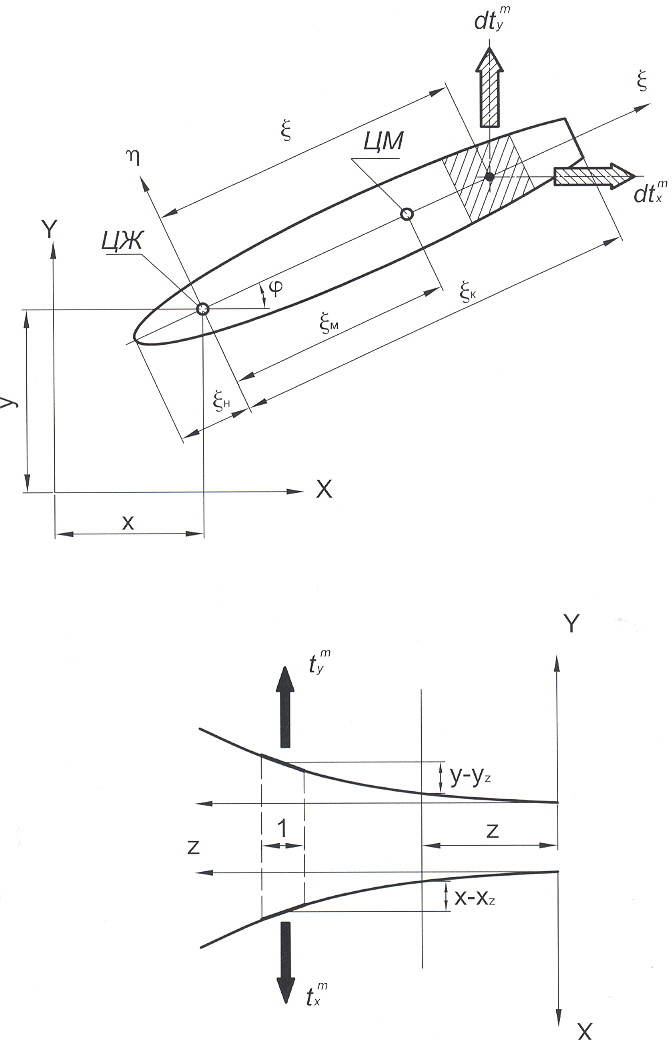
Рис. 2.3.2

Если и - погонные массы стержней (руля и стабилизатора), то погонная массовая нагрузка

, ,

, (2.3.4)

Здесь , ,

- масса единицы площади плоского стержня (руля, крыла)

и погонный массовый момент инерции стержня соответственно

, .

Запишем приближенные моменты и перерезывающие силы деформированных стержней на примере рулевой поверхности в соответствии с (2.2.3)

,

,

,

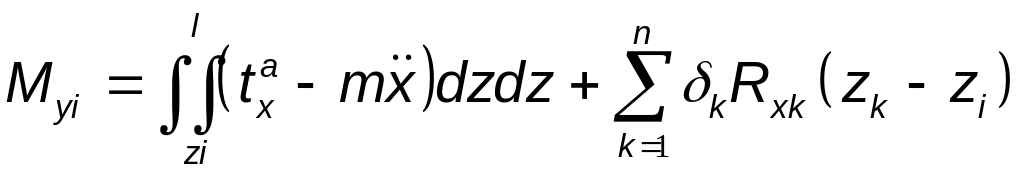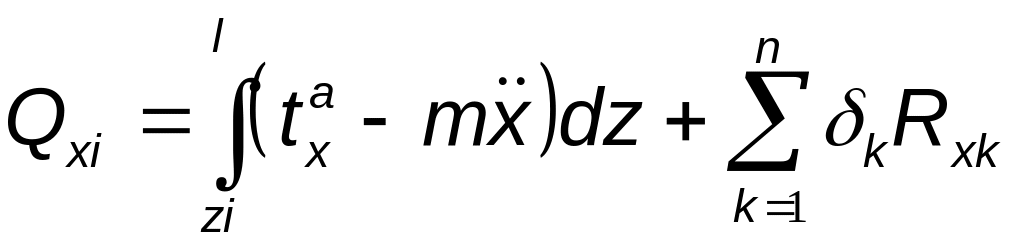(2.3.5)

к которым ещё добавятся константы.

Аналогичные уравнения записываются для стабилизатора.

Выражения (2.3.5), представляющие собой при нижнем пределе интегрирования уравнения равновесия, вместе с условиями совместности(2.2.5), физическими зависимостями Кирхгофа-Клебша (2.1.3), уравнениями связи угловых и линейных перемещений(2.1.7) и связи перемещений x, y ,z с деформациями æ_x ,æ_y,τ_z (2.1.5), записанными для руля и для стабилизатора, составляют разрешающие уравнения движения. Записанные через интегрирующие матрицы и приведенные к системе алгебраических эти уравнения могут быть представлены в виде вектор- функции

(2.3.6)

где .

При численной реализации задачи за исходное приближение неизвестных параметров можно принять их квазистатические значения. Инерционные составляющие при выбираются из физических соображений достаточно произвольно. На первом шаге для вычисления неизвестных можно воспользоваться методом последовательных нагружений, где в качестве шага берется приращение нагрузки при изменении времени .

Тогда, .

На текущих азимутах приближенное решение системы определяется путем использования экстраполяционных полиномов. В качестве примера приведем экстраполяционный полином Ньютона:

.

Для определения векторов и воспользуемся одношаговой процедурой Вильсона, согласно которой для искомых величин можно записать выражения:

;

.

Решение уточняется итерационным методом Ньютона-Канторовича. На рис. 2.3.3 представлен фрагмент решения. Приводится сравнение нормальной и лобовой кривизны руля во времени.

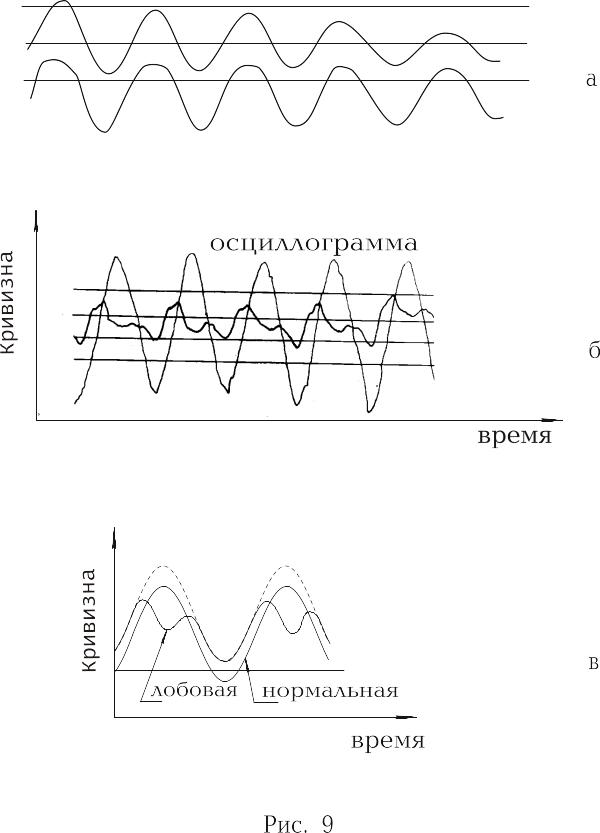
^{Рис 2.3.3}

Детальное обсуждение рис. 2.3.3. приведено ниже вместе с результатами эксперимента.