§ 2.2 Катастрофы составных стержней
Предложенная в §2.1 геометрически нелинейная теория расчета тонких стержней позволяет построить метод исследования силового взаимодействия двух сочлененных поверхностей, таких как руль (элерон) и стабилизатор (крыло) при больших перемещениях. Лишь геометрически нелинейное решение дает возможность найти действительные шарнирные моменты руля, исследовать явление потери его эффективности и катастрофического изменения формы (прощелкивания).
Постановка задачи
Отказ от традиционной расчетной схемы оперения, не учитывающей угол отклонения руля, приводит к новому представлению о взаимодействии двух статически неопределимо соединенных звеньев. На основе новой расчетной схемы выявлено перераспределение реакций , связанное с включением лобовой изгибной жесткости руля и, что самое главное, обнаружены новые силы реакции в плоскости стабилизатора . Эти лобовые реакции, величина которых соизмерима с , сильно изменяют шарнирные моменты руля. Количественно это можно оценить, если провести расчет по деформированной расчетной схеме, приводящей к нелинейным решениям. Более того, наличие сил в срединной плоскости руля может привести к потере устойчивости его "плоской формы" катастрофическому изменению формы (прощелкиванию) [3].
Получим
разрешающие уравнения для расчета
оперения с многошарнирным рулем
(количество шарниров п
более двух) в геометрически нелинейной
постановке. Представим стабилизатор и
руль стержнями переменного по длине,
не изменяемого в процессе деформации
сечения, загруженными произвольной
внешней нагрузкой, в общем случае
зависящей не только от углов отклонения
и установки руля и стабилизатора, но
и от их деформаций. Свяжем оси z
и
с линиями
центров жесткости недеформированных
руля и стабилизатора, оси y
и
направим по нормали к их срединным
плоскостям, а оси x
и
выберем так, чтобы полученные системы
координат были правыми (рис. 2.2.1,а).
Считаем соединения, т.е. кронштейны
навески, жесткими в направлении
, и
и податливыми в направлении оси
шарниров.
Неизвестную
реакцию в i-м
узле
,
считаем лежащей в плоскости деформированного
стабилизатора и направленной по нормали
к оси шарниров,
(если таковая имеется)
по оси шарниров от заделки стабилизатора,
по нормали к плоскости
так, чтобы полученная система
была правой.
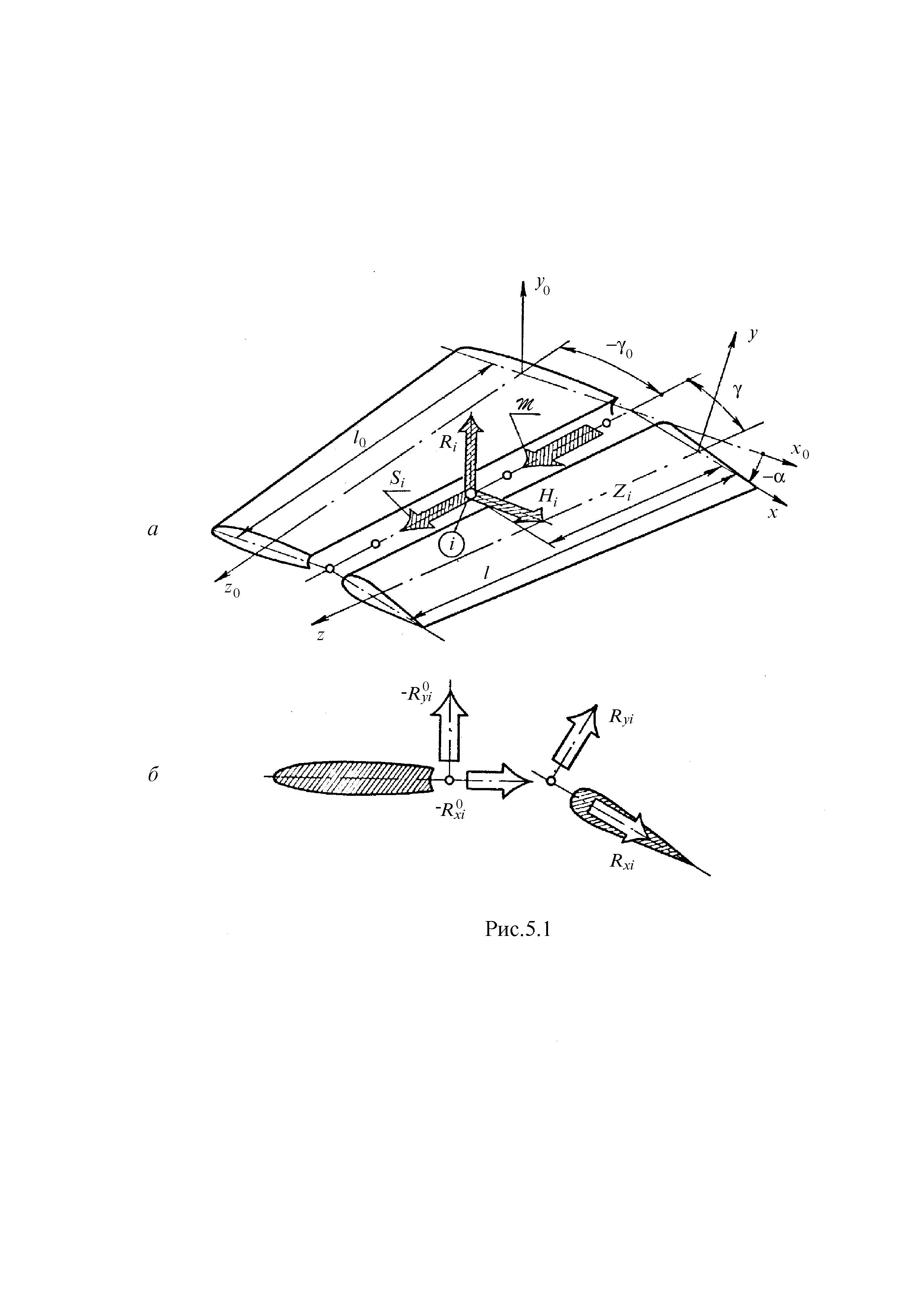
Рис. 2.2.1
Уравнения равновесия
Запишем
уравнения равновесия стабилизатора и
руля, обозначая ноликом, все величины,
относящиеся к стабилизатору. Для этого
необходимо реакции
,
и
,
привязанные к оси шарниров, привести к
осям соответствующего звена (руля и
стабилизатора). Полагаем
,
,
что соответствует экспериментальной
модели.
Для стабилизатора:
-
составляющая реакции в i-м
шарнире, параллельная оси
;
-
составляющая реакции в i-м
шарнире, параллельная оси
;
-
составляющая реакции в i-м
шарнире, параллельная оси
.
Составляющие
реакций стабилизатора можно записать,
используя матрицу Л(2.1.4),
т.е.
,
зависящую от
,
и
,
и матрицу руля Л,
зависящую
от
,
и
.
Эти
матрицы в каждой i-й
точке стабилизатора и руля имеют свои
значения
,
.
Они определяют компоненты реакций в местных осях соответствующих стержней (рис. 2.2.1).
,
(2.2.1)
Чтобы
привести их к одним осям, например, осям
стабилизатора, необходимо связать
реакции
и
через угол отклонения руля.
Запишем выражения погонных подъемных сил и моментов относительно передних кромок стабилизатора и руля [16], в которых нет членов, зависящих от производных перемещений по времени, так как решается квазистатическая задача:
(2.2.2)
Здесь
;
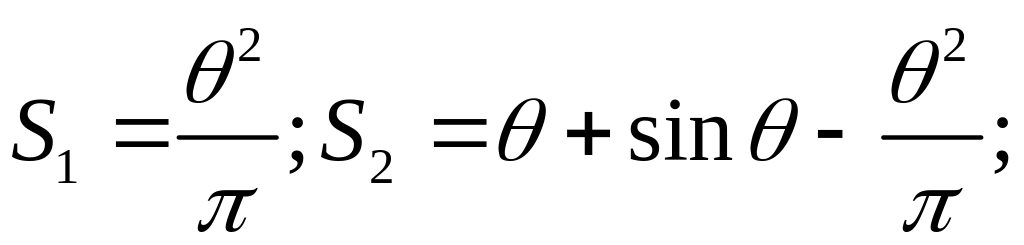
– определяется из соотношения
и
b
– хорды стабилизатора и руля;
+
–
расстояние от передней кромки стабилизатора
до оси вращения руля;
– скорость
набегающего потока,
– плотность
газа
Получим
выражения моментов
а также поперечных сил
в
любом i
-м
сечении для руля
и стабилизатора
по
деформированной расчетной схеме (рис.
2.2.2):
(2.2.3)
M
;
;
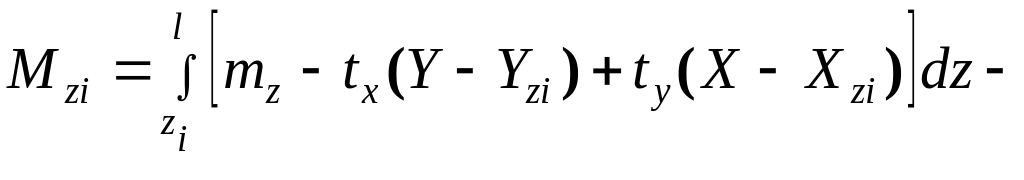
(2.2.3)
;
В уравнениях (2.2.3) опущены некоторые малые члены.
Здеcь обозначено: М – момент в качалке управления,
;
Приравнивая (2.2.1) и (2.2.3) получим уравнения равновесия.
Нумерация шарниров начинается от начала координат:
К = 1,2,3, ..., n ;
нумерация расчетных сечений также начинается от начала координат:
i=1,2,3,...,
;
Рис. 2.2.2
Для определения неизвестных реакций и управляющего момента М можно составить лишь шесть независимых уравнений равновесия руля.
Расчет статически неопределимых оперений требует привлечения условий совместности перемещений, для того чтобы порядок системы разрешающих алгебраических уравнений соответствовал количеству неизвестных.