Большие перемещения стержней

Рассмотрим недеформированное состояние стержня, определяемое на рис. 2.1.2,a точкой М - центром жесткости сечения стержня и ортами центра жесткости у которых имеют начало в центре жесткости, лежат в плоскости сечения стержня и направлены параллельно главным центральным осям сечения, а направлен по касательной к линии центров жесткости сечений в точке М. Триэдр центра жесткости построен по правилу образования правой системы координат.

Рис. 2.1.2

Воздействие произвольной внешней нагрузки превращает ось центров жесткости сечений стержня в некоторую кривую S. Точка М переходит в М^* на кривой S. Триэдр центра жесткости поворачивается, после чего орты, связанные с осями , переходят в положение ^*, ^*, а орт касательной к оси жесткости стержня превращается в ^*. Перемещение триэдра в деформированное состояние можно представить как поступательное из точки М в М^* и некоторый поворот вокруг мгновенной оси.

Поворот триэдра осей xyz в положение можно осуществить с помощью трех последовательных вращений. Это могут быть оси Эйлера, использованные Кирхгофом.

Поворот на угол  ( ) выполним относительно оси i. Новые орты триэдра , полученного после этого поворота, можно записать в виде векторов-строк (рис. 2.1.2б):

₁ = [1, 0, 0] ;

= [0, cоs , sin ] ;

₁ = [0, -sin , cоs ] .

Таким образом, матрицей перехода от ijk к будет матрица вращения:

осуществляющая преобразование координат:

[ ]^т = Л( ) [х, у, z]^т .

Поворот относительно оси j₁ на угол ( ) осуществляется матрицей:

что приводит к осям и формуле преобразований координат:

[ ]^т = Л ( ) Л ( ) [х, у, z]^т .

Третий поворот на угол ( ) относительно оси завершит совмещение триэдров и , определяемых осями, параллельными xyz и .

Матрица этого поворота:

Осуществляя последовательные повороты на углы и , получим матрицу преобразований координат

Л = Л( ) Л( ) Л( ) ,

которая имеет вид:

(2.1.4)

Предположим, что триэдр равномерно перемещается с единичной скоростью вдоль деформированной оси стержня S (рис. 2.1.2,a). Обозначим скорость поворота вектора ^*, связанного с сечением стержня, относительно оси через , скорость поворота ^* относительно - через и соответственно ^* и ^* относительно - через . Это кривизны стержня в двух плоскостях и относительный угол закручивания (предполагаем пока, что цт сечений совпадают с цж).

Выразим вектор угловой скорости через производные углов a, b и j. Рассмотрим два положения триэдра. Первое определяется значениями углов a, b и j, второе углами + d , b + db, j + dj. Можно осуществить переход из первого положения во второе с помощью трех бесконечно малых поворотов, векторы которых запишутся так:

Учитывая, что бесконечно малые повороты подчиняются законам сложения векторов, запишем результирующий вектор поворота

и вектор угловой скорости:

Здесь производная по времени заменена производной по дуге S, т.к. при движении с единичной скоростью dt = ds, и обозначена штрихом.

Проекции на оси, связанные с центром жесткости стержня (а это и будут æ_ξ, æ_η, τ_ζ), выразятся так:

æ_ξ ^*, æ_η ,

Используя матрицу (2.1.4), получим

æ_ξ = a' cos b cos j + b' sin j;

æ_η = - a' cos b sin j + b' cos j; (2.1.5)

= a' sin b - j'.

Положение точки на оси стержня определяется радиусом-вектором

(2.1.6)

Углы поворота можно связать с перемещениями Х , Y , Z , считая, что элемент дуги ds совпадает по направлению с ортом ^*:

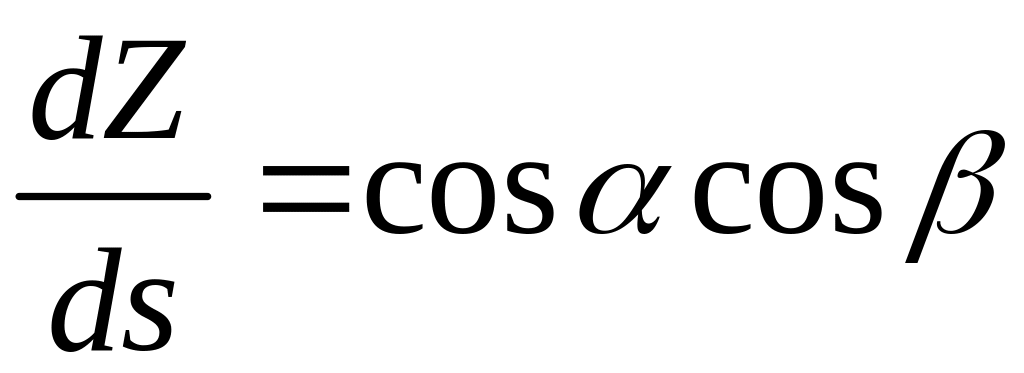. (2.1.7)

Неизвестные a, b и j, определяющие перемещения (2.1.7), можно найти из решения нелинейной системы (2.1.3), подставляя в нее (2.1.5) и выражая

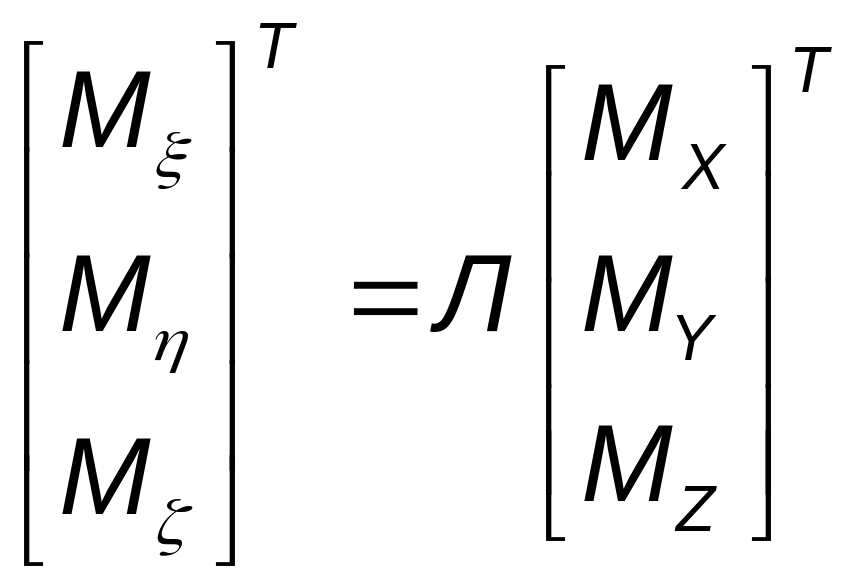(2.1.8)

Моменты М_x , М_y , М_z определяются с учетом упругих перемещений Х,Y,Z .

Таким образом, поставленную проблему можно считать разрешимой в больших перемещениях. Многие задачи авиационной техники, такие, как моностержни (крыло, стабилизатор, киль) могут быть с достаточной степенью достоверности решены при

sin a = a, sin b = b, sin j = j ,

cos a = cos b = cos j = 1.

В этом случаев матрица (2.1.4) примет вид:

Из (2.1.7)

,

на основе чего

В результате получим

Эта теория может быть названа теорией конечных перемещений, которая учитывает не только конечность перемещений, но и предполагает их малость.

Можно сказать, что основы теории конечных перемещений заложены в работах Прандтля. Тимошенко использовал ее при исследовании задач устойчивости плоской формы изгиба балок в варианте

От теории Кирхгофа, использующей углы Эйлера, не удается перейти к уравнениям Прандтля. Их можно получить, если при выводе выражений 2.1.4 и 2.1.5 использовать предположение о малости a, b и j, и следовательно, записать вектор поворота триэдра в виде:

Тогда

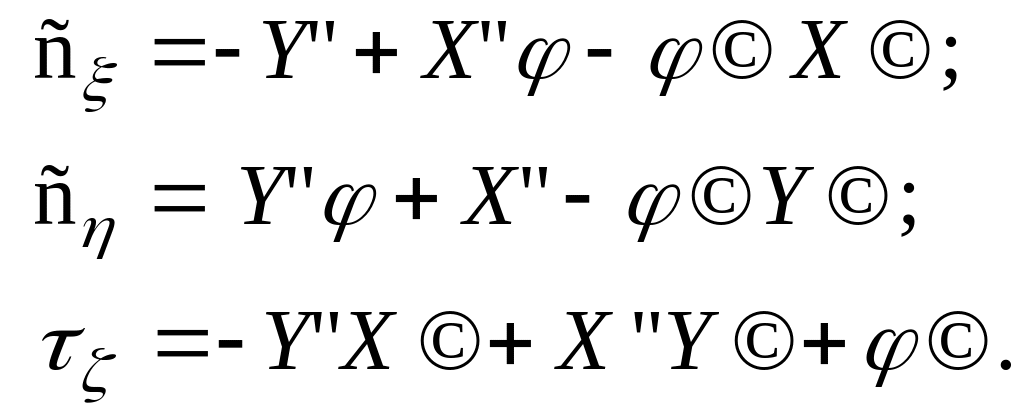
Уравнения Прандтля использовались В.П. Ветчинкиным для определения взаимосвязанных перемещений в геометрически нелинейной задаче расчета крыла. С.П. Тимошенко удалось привести исследуемую задачу "об устойчивости плоской формы при изгибе балки" к линейной и решить до конца. При решении задач устойчивости в малом это не привело к заметной ошибке. Решение задач на основе теории конечных перемещений может привести к значительным ошибкам, и тем большим, чем больше эти перемещения. И это в полной мере относится к катастрофам составных стержней типа оперения с рулем и крыла с элероном, где перемещения действительно большие.

Осталось записать , и - моменты в сечении z от внешних нагрузок и , вычисленные относительно осей, параллельных неподвижным xyz, в расчетном сечении. Для построения моментов по деформированной расчетной схеме на рис. 2.1.3 стержень изображен в трех проекциях. Прогибы линии ц.ж. стержня в неподвижных осях для сечения, где приложена внешняя нагрузка и обозначены через Х и Y , а для расчетного cечения - через и , углы закручивания соответственно - через и .

Рис. 2.1.3

Изгибающие моменты запишутся так же, как и при расчете по недеформированной расчетной схеме, т.е.

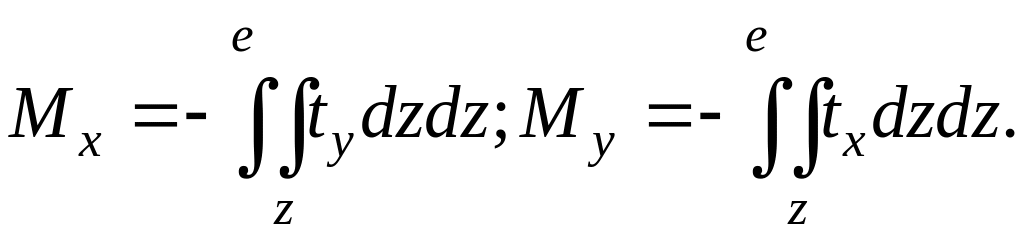(2.1.9)

Момент относительно оси z создается всей нагрузкой, перенесенной на ось z в пределах от z до l :

(2.1.10)

где - погонный момент внешней нагрузки, найденный без учета перемещений.

Перемещения X и Y находим интегрированием уравнений (2.1.7)

Перерезывающие силы и проходят через центр жесткости, и для их записи необходимо использовать матрицу

(2.1.11)

Нули в этом уравнении могут быть заменены растягивающими силами стержня и .

Выражения (2.1.3)-(2.1.10) представляют собой разрешающую систему уравнений стержня при больших перемещениях. Решаем её, превращая в алгебраическую, методом интегрирующих матриц[5].

Полученная система

(2.1.12)

имеет вектор неизвестных