§2.1. Геометрически нелинейная теория равновесия стержней. Постановка задачи
Авиационные конструкции, для расчета которых будет построена геометрически нелинейная теория, могут быть представлены прямолинейными до деформации стержнями, не имеющими предварительной закрученности. Это конструкции большого удлинения, имеющие довольно частый поперечный силовой набор (поэтому для них с достаточной степенью точности может быть принята гипотеза о неизменяемости формы поперечного сечения), конструкции монолитные или тонкостенные, все элементы которых работают в пределах закона Гука. При необходимости по предлагаемой теории можно рассчитать конструкцию и за пределами упругости, а также после потери устойчивости продольных элементов, например, методом редукционных коэффициентов, последовательными приближениями корректируя приведенные характеристики сечения стержня.
Перемещения стержня считаем большими, т.е. достигающими нескольких толщин, но большими не настолько, чтобы можно было усомниться в справедливости гипотезы о плоскостном распределении относительных удлинений при изгибе. Следовательно, для малого элемента деформированного (искривленного и закрученного) стержня, можем записать:
æ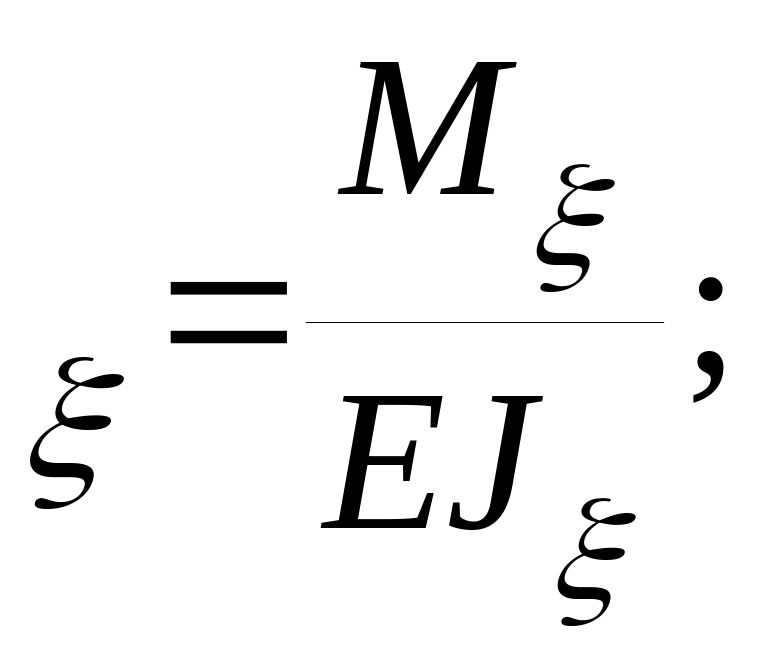
æ
(2.1.1 )
Эти
соотношения принято называть уравнениями
Кирхгофа-Клёбша. Здесь
,
-
кривизны линии центров тяжести сечений
в плоскостях h
и x
;
- относительный
угол закручивания оси
;
,
- изгибающие
моменты, вычисленные относительно осей
и
;
- крутящий
момент сечений;
- изгибные жесткости, вычисленные
относительно осей
и
;
- жесткость
на кручение.
На
рис. 2.1.1,а
изображены главные центральные оси
,
образующие
с осью
подвижный триэдр правой системы
координат, и оси
,
начало которых совпадает с центром
жесткости сечения, а ось
для крыльевого профиля - общая с главным
центральным триэдром
.
Будем называть систему
триэдром центра жесткости. Расстояние
между двумя охарактеризованными
триэдрами обозначим через
и будем
считать его положительным, если центр
тяжести (цт) расположен на положительной
координате осей триэдра жесткости, как
изображено на рисунке.
Р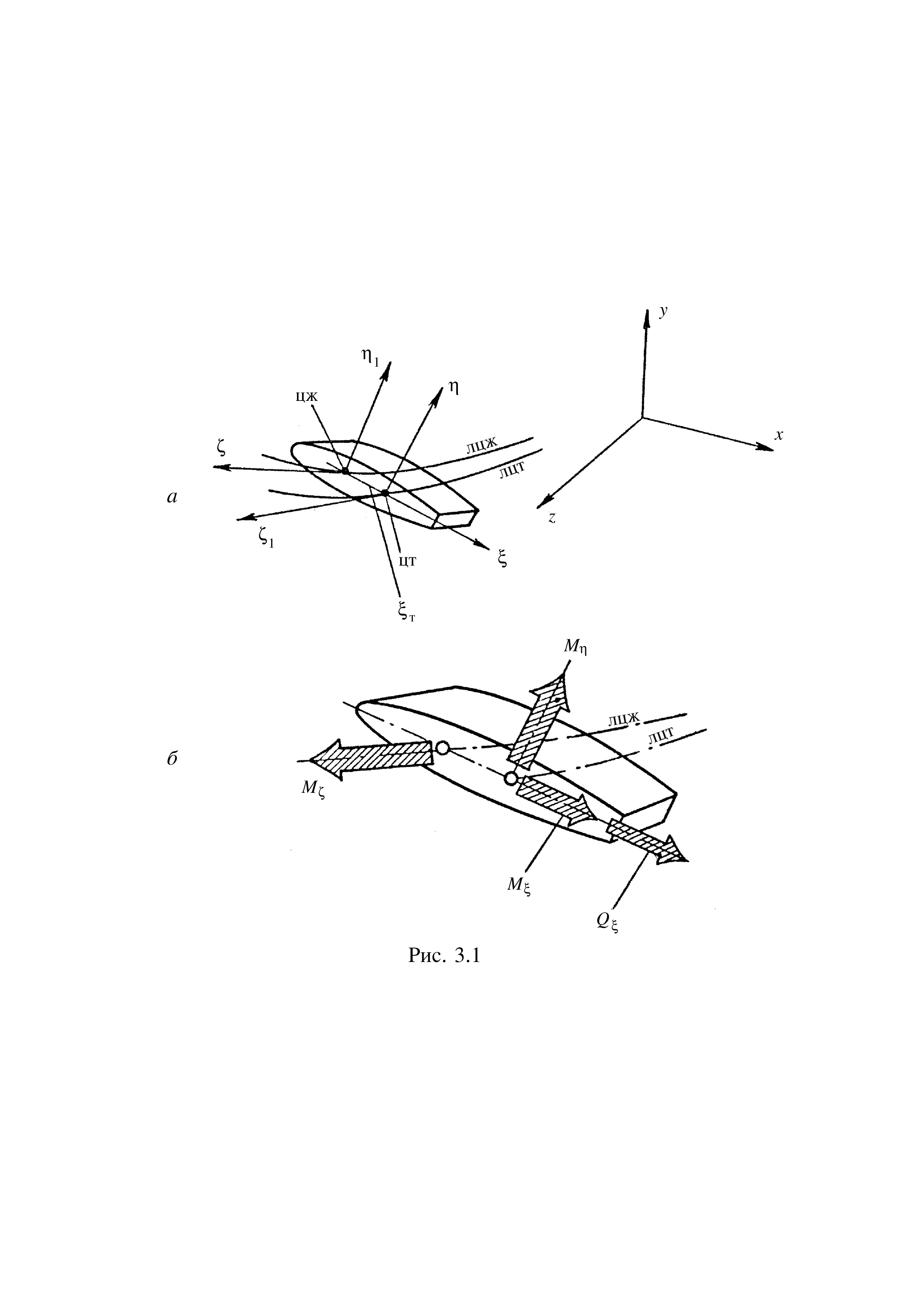
ис.
2.1.1
Два
первых соотношения (2.1.1) справедливы
для случая исследования тонких длинных
стержней. Стержни крыльевого профиля
в плоскости
не всегда можно считать таковыми, для
них значение
будет зависеть не только от
,
но и от перерезывающей силы
в плоскости
, т.е. следуя С.П. Тимошенко, запишем:
æ
(2.1.2)
где S - кривая, представляющая собой линию центров тяжести сечений стержня;
-
касательное
напряжение в районе
цт сечения,
вызванное
силой
;
G - модуль сдвига.
Третье
соотношение (2.1.1) развивалось работами
С.П. Тимошенко, В.В. Власова,
А.А. Уманского и др., но мы это будем
учитывать лишь введением эффективной
жесткости
[5].
Для малого элемента стержня мы будем использовать следующие соотношения между нагрузками и деформациями, основанные на гипотезе о неизменяемости формы сечения:
æ
æ
(2.1.3)
Такой подход не позволяет учитывать влияние вырезов, разъемов, неполных заделок, сосредоточенных сил и моментов на перемещение оси стержня. При наличии таковых в рассматриваемых нами конструкциях мы будем определять "эффективные" жесткости стержня в зонах возмущений напряженного состояния, как это описано в [5].
Далее,
для того чтобы связать малые элементы,
деформации и нагрузки которых записаны
в местных (для каждого элемента своих)
осях
и
,
необходимо все их привести к одной
системе координат. Для приведения к
неподвижной системе xyz
будем
использовать матрицу направляющих
косинусов углов между осями отдельного
элемента стержня и осями этой системы.