§ 4.5 Формула Больцмана

Это тоже некоторое распределение, только для частиц в силовом поле.

Рассмотрим вторую часть распределения Максвелла-Больцмана (3.17, а).

dW ( ) = · 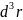или

F {U (x,y,z)} = – функция распределения.

Учитывая, что dW ( ) = для числа частиц в элементе объёма

dV = = dx·dy·dz запишем:

dN = · dx·dy·dz

Для частиц воздуха в приповерхностном слое земли U(x,y,z) = U(z)= mgz. Считая, что n_o = для концентрации n = имеем:

n (x,y,z) = n_o (3.24)

Последнее выражение называют формулой Больцмана. Для частиц Учитывая связь концентрации с давлением ( p =nkT - уравнение состояния), приходят к барометрической формуле

p (z) = n_o ,

определяющей изменение давления с высотой в столбе воздуха.

ψ → ω → dW δQ

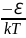
δ = ω_o² = 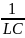cos Ω⁽ⁱ⁾

    α φ q φ_o β ω ω_о 2 π ψ

§ ℓ δ λ φ ε θ α π υ ν ω τ μ γ _x

ψ ρ ∙ § ΄ М_z

→ ∶ § π tg φ ψ → ω → ℏ

δ = ω_o² = cos(ωt + φ_o) sin (ωt + φ_o) const

е^{- δt} ω = ε_{m рез} pV = νRT = νkNT,