
- •§ 1.1 Основные положения ст.Ф.
- •§ 1.2 Флуктуации и средние значения
- •§ 1.3 Основной постулат статистической физики
- •§ 1.4 Статистический вес (1.4.1) и энтропия (1.4.2)
- •§ 2.1 Состояние макросистемы и процесс
- •§ 2.2 Первое начало термодинамики. Химический потенциал и внутренние параметры
- •§ 2.3 Второе и третье начала термодинамики. Теплоёмкость
- •§ 3.1 Распределение Гиббса
- •§ 3.2 Квантовые статистики Ферми-Дирака и Бозе-Эйнштейна
- •§ 3.2.2. Статистика Бозе-Эйнштейна
- •§ 3.3 Плотность состояний
- •§ 4.1 Переход от квантовых распределений к классическому
- •§ 4.2 Критерий вырождения для квазисвободных частиц
- •§ 4.3 Распределение Максвелла – Больцмана
- •§ 4.4 Распределение Максвелла (р.М.)
- •§ 4.5 Формула Больцмана
§ 4.1 Переход от квантовых распределений к классическому
Очевидно, что стирание различий между фермионами и бозонами эквивалентно отказу от квантового рассмотрения, т.е. откату на классические позиции. Формально это получается, если пренебречь 1 в знаменателе функций fF и fB . Получим:
fF
=
fB
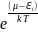 =
fкл.
= fБ
=
fкл.
= fБ
Это возможно, если экспонента в знаменателе много больше 1. Квазиклассическое (классическое) распределение носит имя Больцмана.
fБ = (3.15)
.
fБ
=
N
(ℇi
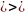 1 – среднее
число частиц в каждом i
состоянии мало.
1 – среднее
число частиц в каждом i
состоянии мало.
Выражение
(3.15) имеет вид, соответствующий
распределению Гиббса (3.2), если принять
C =
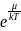 .
.
§ 4.2 Критерий вырождения для квазисвободных частиц
Традиционно в физике говорят о вырождении уровней энергии (состояний) и о вырождении самой системы.
Имеются определённые критерии в каждом случае.
Если энергия системы частиц (соответственно и каждой частицы) слабо зависит от температуры, то система является вырожденной.
Условие
fF = fB (*)
является критерием, что система частиц будет классической
( N (ℇi 1 ) . Это эквивалентно условию
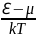 1 (**)
1 (**)
Что, в силу справедливости утверждения 0 ℇ , даёт дополнительные условия:
– μ / kT 1
μ 0
׀ μ ׀ kT
Выражение (3.8) позволяет при заданном числе частиц N определить значение химического потенциала невырожденного ансамбля и дать дополнительные критерии. Итак:
μ
=
k
T· ln
(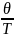 ),
),
где
θ =
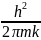 (γs
n)3/2
(γs
n)3/2
- параметр, имеющий размерность температуры.
При концентрации частиц равной критической n nc характеристическая темп-ра θ = θкр. и классическая статистика даёт весьма приближённые результаты.
Она применима при
n
nc
= γs
(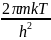 )3/2
)3/2
или θкр. Т.
Можно показать, что условием подобным концентрационному является соотношение
λ Б l,
где λ Б - длина волны де Бройля и l – расстояние между частицами. В противном случае система является вырожденной.
§ 4.3 Распределение Максвелла – Больцмана
Вернёмся к распределению Больцмана (3.15)
Ni
=
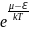 1
1
Для числа частиц находящихся в состояниях dΩ имеем:
dN = Ni ·g(ℇ)·dℇ = Ni · γs dΩ
Подставляя в экспоненту значение хим. потенциала
μ = k T· ln )3/2 ] (3.16)
получаем:
dN
=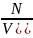 ·
·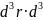 p
p
Если энергию частиц можно представить в виде суммы кинетической и потенциальной энергий
ℇ =
ℇк
+ U(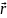 )
)
dN
=
·
|
Под U( ) можно понимать энергию частиц в каком-либо силовом поле.
Мы пришли к известному классическому распределению Максвелла – Больцмана.
Здесь
ℇк
=(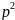 /2m)
=
/2m)
=
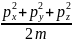 -
кинетическая
энергия.
-
кинетическая
энергия.
Выражение (3.17) фактически распадается на два независимых распределения:
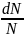 = dW
(
= dW
(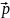 ,
)
= dW(
)
dW (
)
(3.17,а)
,
)
= dW(
)
dW (
)
(3.17,а)
§ 4.4 Распределение Максвелла (р.М.)
4.4.1 Р.М. по векторам импульса и скорости, и их проекциям
Имеем из (3.17, а)
dW(
)
=
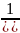 d
d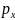 d
d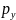 d
d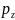 =
F(
)
=
F(
)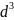 p
(3.18)
p
(3.18)
Оно определяет вероятность обнаружить частицу в заданном элементе импульсного пространства.
F(
) =
=
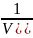 (3.18,a)
(3.18,a)
F(
)
=
F(
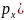 ·
F(
·
F(
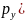 ·F(
·F(
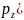 ,
,
причем каждое вида:
F( =
Зная связь импульса, скорости и энергии, получают целый ряд распределений (распределение Максвелла многолико!).
dW(
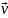 )
= F(
)·d3
)
= F(
)·d3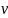 = F(
)·d
x
= F(
)·d
x
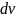 y
z
y
z
Распределение Максвелла по вектору скорости:
F( ) = (3.19)
F( ) = F( x)· F( y)· F( z)
Распределение Максвелла по проекции скорости:
F( x) = (3.20)
Его
называют одномерным. Причём возможна
замена x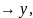 z
z
Трёхмерная
и одномерная функции нормируются на 1
при интегрировании в пределах изменения
переменной от -
до +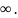 Вид F(
x)
для двух
температур приведен на рис.
Вид F(
x)
для двух
температур приведен на рис.
4.4.2 Р.М. по модулям импульса и скорости
Используя выражение dΩ в импульсном пространстве
dΩ
= V·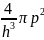 dp,
dp,
получают по схеме аналогичной для получения (3.18) и (3.18,а),
выражение для распределения по модулю импульса:
F(
p)
=
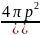 (3.21)
(3.21)
Переход от F( p) к F( ) с учётом, что p = m и dp =md даёт:
F(
)
=
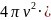 (3.22)
(3.22)
Вид последнего распределения показан на рис. для двух разных температур.
Используя F( ), находят среднеарифметическое и среднеквадратичное значения скорости:
υ
=
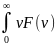
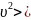 =
=
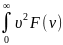
Для частиц (молекул) идеального газа
υ
=
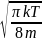 и
и
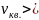 =
=
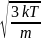 ,
,
причём
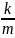 =
=
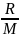 , где R
- газовая постоянная, М – масса моля.
, где R
- газовая постоянная, М – масса моля.
Наиболее вероятное значение скорости находится из условия экстремальности функции:
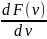 =0
откуда:
в
=
=0
откуда:
в
=
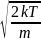 .
.
4.4.3 Р.М. по энергии частиц
Прямой путь получения ф.р. - из соотношения (3.17) для dN через вероятность dW с использованием распределения Больцмана - (3.15) и химического потенциала - (3.16).
При этом для dΩ используем (3.13).
g (ℇ)
dW
= F(ℇ)
dℇ
F(ℇ)
=
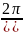 (3.23)
(3.23)
Вид распределения (3.23) приведен на рис. для двух разных температур.
Используя его, легко найти среднюю энергию частицы и её наиболее вероятное значение:
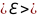 =
kT
и ℇв
=
kT
=
kT
и ℇв
=
kT
Здесь 3 = i - числу степеней свободы. Тогда очевидно, что энергия, приходящаяся на одну степень свободы, равна kT.

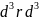 p
(3.17)
p
(3.17)