§ 2.3 Второе и третье начала термодинамики. Теплоёмкость

По Клаузиусу отношение 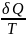определяет приращение энтропии dS.

S – функция состояния системы; 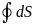= 0.

Условие δQ = 0 (адиабатический процесс) эквивалентно условию

S = const

Конечное изменение энтропии в равновесном, обратимом процессе

S = S₂ – S₁ = 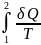(2.3′)

Соответственно для кругового процесса: 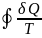= 0.

2.3.1Закон возрастания энтропии. Второй з-н термодинамики.

Если замкнутая система некоторое время находилась в неравновесном

состоянии, то вероятным ходом будет переход в состояние с большим статистическим весом, т.е. с большей энтропией.

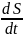
Энтропия замкнутой системы может либо оставаться неизменной, либо монотонно возрастать, достигая максимального равновесного значения (  0).

Символически так: S 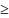0, (2.3)

где равенство для равновесной системы.

Для целой системы, состоящей из подсистем при наличии флуктуаций

δS₁ + δS₂ = δS  0

Роль (2.3) очень велика. Он показывает направленность поведения системы.

Втрое начало в термодинамике эквивалентно утверждению о невозможности вечного двигателя второго рода: Невозможно создать устройство совершающее положительную работу без изменений в окружающих телах. Или: невозможен самопроизвольный переход теплоты от менее нагретого тела к более нагретому телу.

2.3.2. Теплоемкость

Величину 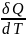= C называют теплоёмкостью. Она определяется как количество теплоты, которое необходимо сообщить системе, чтобы увеличить её температуру на один градус.

Различают:

( _v= C_v и ( _р= C_р и удельные теплоёмкости: с_р =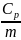 и с_v =

и молярные:

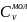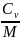= и 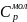= 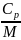, где М – масса моля.

Выражение (2.3′) можно записать

S = 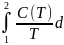Т

Теплоёмкость идеального газа

Для V = const

δA′ = pdV =0, dℇ =dQ

Для одноатомного газа

ℇ = 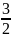kNT  ( _v= C_v kN = ν R  = R

+ R = - закон Майера. 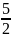 = R

Отношение

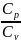= γ - постоянная адиабаты  pV ^γ = const

γ = 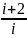, где i - число степеней свободы.

2.3.3. Объединённая форма первого и второго начал термодинамики.

Если система не успевает приходить в равновесие

dS = dS₁ + dS₂ (*)

dS₁ = и dS₂ – приращение за счёт перехода к равновесности (dS₂  0)

Тогда: S = S₂ - S₁

Подставляя dS из (*) в (2.2) получим:

dℇ 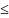Т dS - pdV + μdN (2.4)

Здесь знак = относится к обратимым, а знак к необратимым процессам.

2.3.4. Третье начало (теорема Нернста)

Энтропия может быть установлена только с точностью до постоянной.

S_Сист. = 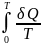+ S₀

Нернст и затем Планк, исходя из опыта, показали, что

S_Сист. → 0, когда T→ 0 (2.5)

Док-во основано на том, что в основном состоянии (с наименьшей энергией) Ω =1 и S =0.

2.3.5. Условия равновесия контактирующих систем

Пусть имеем две системы, которые рассматриваем как подсистемы равновесной системы. В силу аддитивности:

ℇ = ℇ₁ + ℇ₂ = const

V = V₁ + V₂ = const

N = N₁ + N₂ = const

Таже: S = S_max

Эти величины могут флуктуировать, но dℇ₁ = - dℇ₂

Анализ показывает, что условием теплового равновесия является

Т₁ = Т₂ (2.6)

для всех частей макросистемы.

В более общем случае термодинамического равновесия требуется, чтобы

р₁ = р₂ и μ₁ = μ₂

т.е. равенство давлений и термодинамических потенциалов контактирующих тел.

Гл. 3 ФУНКЦИИ РАСПРЕДЕЛЕНИЯ В РАВНОВЕСНЫХ СИСТЕМАХ

Нахождение таких функций - основная задача статистики.