4. ОСНОВЫ СТАТИСТИЧЕСКОЙ ФИЗИКИ И ФИЗИКИ ТВЁРДОГО

ТЕЛА

ВВЕДЕНИЕ

1. Предмет статистической физики.

Предмет нашего изучения: Раздел физики, цель которого выразить свойства макроскопических тел через свойства и взаимодействия частиц, образующих макросистему. Иначе – СТАТИСТИЧЕСКАЯ ФИЗИКА.

Чисто квантовое или чисто классическое описание систем большого числа частиц ( 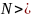10⁵ ) не проходит.

«Новая физика» - на базе статистического подхода.

Описание основано на использовании средних величин и связей между ними.

Достаточно небольшое число таких величин, называемых макропараметрами системы, определяемых с использованием функций распределения (Ф.Р.) - F(X).

Нахождение Ф.Р. – основная задача статфизики.

Математический аппарат – теория вероятностей.

Выводы феноменологической науки - термодинамики естественным образом вытекают из статфизики.

ЛИТЕРАТУРА:

1. Егорова Т.С., Жилинский А.П., Мискинова Н.А. “Основы статистической физики и физики твёрдого тела”, МТУСИ, М., 2008.

2. Савельев И.В. “Курс физики”, т.т. 1,3; М., Наука, стерео.

3. Трофимова Т. “Курс общей физики”, М., В.Ш., 1998.

Функция распределения плотности вероятности

F(X) =

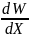
Смысл отношения: Это вероятность на единичном интервале изменения переменной.

Отсюда следует условие нормировки:

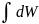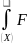= (X)dX = 1

Среднее физ. величины

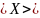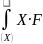= (X) dX

Для системы из N частиц вводится такая f(X) , что

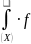(X)dX = N

Будем исходить из того, что:

1. наиболее последовательное описание – на базе квантовой физики;

2. связь между макропараметрами задаётся уравнением состояния (Клайперона – Менделева).

При этом различают внешние и внутренние макропараметры.

Одному макросостоянию обычно отвечает несколько (и очень много) доступных микросостояний. Изменение макросостояния называют процессом.

Гл.1 ЭЛЕМЕНТЫ СТАТФИЗИКИ РАВНОВЕСНЫХ СОСТОЯНИЙ

§ 1.1 Основные положения ст.Ф.

1.1.1 Фазовое пространство – многомерное пространство осями которого служат оси обычного евклидового пространства и оси проекций ипульсов частиц (возможны и другие переменные).

Состояние системы задаётся точкой в Ф.П.

Движению соответствует фазовая траектория.

Для одной частицы Ф.П. – 6 ^ти мерно; для N частиц 6 ^N мерно.

Элементарный объём в таком Ф.П.

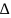Г = x z p_x p_{y 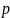z} = ³r · ³p

Мерность пространства γ = 2iN , где i- число степеней свободы.

Г = 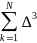r_k ³ p_k

Минимальный объём в Ф.П. квантовой системы для одной частицы равен 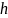³. Для N частиц ^3N.

Число возможных квантовых микросостояний в конечном элементе Г

= (*)

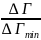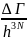Число доступных микросостояний системы, определяемых подобно (*) называют её статвесом Ω.

2. Вероятность и функции распределения

Если dt - часть полного времени наблюдения τ нахождения подсистемы в некотором Г, тогда

dW =

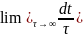
называют вероятностью нахождения подсистемы в одном из состояний из элемента Ф.П.

Коэффициент пропорциональности между dW и dГ, зависящий от координат и импульсов, и представляет функцию распределения.

Условие её нормировки

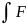(r_k, p_k) d³r_k d³p_k = 1

В равновесном состоянии ни вероятность, ни функция распределения не зависят от времени. Сложнее, когда система релаксирует, нет равновесия.

Усреднение по времени заменяют усреднением по статистическому ансамблю. Ст. ансамбль набор одинаковых подсистем, состояние каждой из которых в Ф.П. изображается всего одной точкой.

В случае, когда система состоит из двух подсистем и

dW₁ = F₁ (r_k1, p_k1) d³r_k1 d³p_k1

и вероятность

dW₂ записывается аналогично заменой индекса 1 на 2

Вероятность появления одновременного события

dW₁₂ = dW₁ ·dW₂

В случае N подсистем

dW₁₂ = dW₁· dW₂ …. dW_N

Это приводит к тому, что Ф.Р. всей системы равна произведению Ф.Р. для всех подсистем.

§ 1.2 Флуктуации и средние значения

Мгновенные и случайные отклонения (например, числа частиц N) от среднего называют флуктуациями. Может принимать как положительные,

так и отрицательные значения и N → 0 при t → .

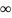Для аддитивной физ. величины среднее значение флуктуации равно нулю:

X = (X - X ) = 0

Заметим, что в качестве среднего X используют

X = 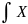·F(p,q)dp·dq =

= ·F₁· F₂ ·F₃ … F_n ·dq₁·dq₂·dq₃… dq_n·dp₁·dp₂·dp₃…·dp_n

Следует учесть, что для каждой F_i выполняется условие нормировки.

В качестве меры отклонения от среднего используют среднюю квадратичную флуктуацию α_Х = .

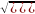В ходу относительная флуктуация

δ =

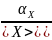
Причём оказывается, что δ = 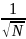, - число частиц системы.

§ 1.3 Основной постулат статистической физики

Смысл равновероятности событий позволяет утверждать, что результат будет тем же, если исследованию подвергать систему в течение некоторого времени или, наоборот, одновременно испытанию подвергать много её подсистем (статистический ансамбль).

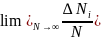= W_i

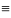= W_i W_ε(i)

Квантовая система с равной вероятностью пребывает в любом из доступных состояний (микросостояний) с заданной энергией ℇ (при равновесии).

Постулат утверждает:

Любые микросостояния, принадлежащие одной энергии – равновероятны.

Например: появление электрона в одном из s или p состояний равновероятно.

Следствия:

1. Если замкнутая система с равной вероятностью обнаруживается в любом из доступных микросостояний, то она находится в равновесии.

2. Замкнутая система при одном значении ℇ будет больше находится в том макросостоянии, которому соответствует большее число микросостояний.