1. Понятие об искусственном интеллекте и экспертных системах.

Логическое программирование базируется на логике и принципах искусственного интеллекта. Основным вопросом логики является выявление механизмов в человеческом мышлении, с помощью которых осуществляется вывод истинных знаний.

В качестве основного языка логического программирования применяют язык логики предикатов первого порядка. Современный этап развития логики связан с наличием следующих её ветвей, относящихся к математической логике: 1) логика высказываний, исчисление высказываний; 2) логика предикатов, исчисление предикатов; 3) теория алгоритмов.

Понятие искусственного интеллекта было введено Маккарти в 56 году.

Под искусственным интеллектом понимают научное направление, которое занимается имитацией (моделированием) мыслительной деятельности человека с помощью вычислительных средств, компьютера, робота.

Строгое понятие интеллектуальных задач дать затруднительно. К ним можно отнести задачи, решаемые в условиях неполноты данных, не чётко сформулированные или сформулированные в общих чертах, проектные задачи, задачи конструирования алгоритмов, доказательство теорем.

В настоящее время принципы искусственного интеллекта используются в областях:

1. автоматическое доказательство теорем;

2. робототехника;

3. автоматизация проектирования;

4. общение человека с ЭВМ на языке, близком к естественному;

5. распознание образов и изображений;

6. лингвистика;

7. теория построения формализованных языков;

8. диагностика;

9. теория игр;

10. прогноз погоды;

11. экспертные системы;

12. системы обработки и получения данных.

Одна из важнейших сфер применения – экспертные системы.

Экспертные системы – системы, сочетающие ЭВМ и специалистов в какой-то области. Это диалоговые компьютерные системы, оперирующие базой знаний в некоторой области и обеспечивающие ответы на запросы пользователя с помощью средств вывода. Знания, представленные в формализованном виде, могут пополняться. Основные компоненты типичной экспертной системы являются: базы знаний, средства логического вывода, интерфейс пользователя.

Центральным моментом любой системы искусственного интеллекта (экспертной системы) является база знаний – описывает предметную область.

2. Понятие о базах знаний. Средства описания и представления знаний.

База знаний – это совокупность сведений заданной предметной области, представленных в формализованном виде.

Человек получает знания различными способами: изображения, схемы, чертежи, таблицы, факты, методы, алгоритмы, законы, правила.

Можно отметить следующие типы знаний:

1. понятийные – в виде набора понятий;

2. структурные – знания о структуре объекта, компонентах и взаимосвязи;

3. процедурные – алгоритмы, программы, методы;

4. фактографические – таблицы, базы данных.

Все знания можно представить как декларативные – описывают предметную область и процедурные – описывают процессы предметной области. Деление носит условный характер, так как в декларативных описаниях могут быть элементы процесса, а в процедурных – элементы описания.

База данных не ориентирована на возможность вывода новых утверждений, это просто информация о свойствах. В базе знаний данные структурированы и взаимосвязаны. База знаний предполагает описание процессов вывода новых истинных утверждений. База знаний – это истинное утверждение, которое описывает свойства отношений в заданной предметной области. Средства базы знаний позволяют применять средства (правила) логического вывода, имеют содержательную интерпретацию некоторого предмета.

Отличительные характеристики базы знаний:

1. База знаний представляет свойства и отношения между объектами предметной области;

2. имеют содержательную интерпретацию в некоторой предметной области;

3. позволяет применять правила логического вывода;

4. языки приближаются к естественному;

5. Сведения баз знаний являются истинными утверждениями.

Средства описания и представления знаний:

• формализованные логические системы;

• языки программирования:

• процедурные (Си, Паскаль);

• объектно-ориентированные;

• декларативные

Декларативные языки – специально ориентированны на искусственный интеллект и являются языками логического программирования. Они предназначены не для описания процедурного решения задач, а свойств предметной области.

Под логическим программированием понимают конечное множество фактов и правил, задающих свойства и отношения между объектами и описывающими истинные утверждения. В фактах и правилах описывается логическая модель предметной области, отношения предметов и правила получения новых свойств.

Логическая программа задаёт множество следствий, которые являются результатом программы. Вычисление логической программы – вывод следствия из него. Это некоторое описание.

Сейчас существует множество языков декларативного программирования. Первыми языками были Lisp (1952) и РЕФАЛ - решение функций алгебры логики (МГУ). SNOBOL, QLISP, PLFNNER, QA-U, SMALLTALK, PROLOG и др. Ориентированные на фреймы: FRL, KRL, KRC.

3. Формы представления знаний. Логические модели. Логика высказываний. Интерпретации. Эквивалентные преобразования сложных высказываний. Правила преобразований.

Формы представления знаний:1) семантические сети; 2) фреймы; 3) логические модели;

4) системы продукции; 5) реляционные.

Основное назначение – формальное описание предметной области с целью возможности применения механизмов вывода из этих описаний новых сведений.

Выбор нужной системы определяют следующие требования:

1. простота и наглядность;

2. наличие средств эквивалентных преобразований;

3. возможность логического выбора;

4. возможность пополнения знаний;

5. универсальность средств;

6. обладание свойством полноты описания.

Требования противоречивы.

В общем виде логические модели можно представить в виде четвёрки LM=<T P A F>, где T – множество базовых элементов; P - множество синтаксических правил построения и выражения из Т; A - множество исходных истинных утверждений; F – множество правил вывода. В рамках этой модели существует разделение: логика высказываний, исчисление высказываний, логика предикатов, исчисление предикатов.

В логике высказываний рассматриваются простые и сложные высказывания. Простые высказывания являются неделимыми объектами, имеющие только 2 значения – истина или ложь. Они обозначаются прописными латинскими буквами. Сложные высказывания образуются из простых с помощью логических операций, и представляются формулами, называемые формулами алгебры-логики или пропозициональными формулами.

Пример: если станок закончил работу, робот грузит кассету с деталями на робокар, который перевозит их на склад, где штабеляр помещает кассету в ячейку.

F₁— станок закончил работу; F₂— робот помещает кассету с деталями на робокар;

F₃—робокар перевозит кассету на склад; F₄— штабелер помещает кассету в ячейку.

Если, то: F₁F₂F₃F₄.

Всевозможные наборы значений логических переменных, входящих в формулу, называется интерпретацией формулы = 2ⁿ, где n – число логических переменных, входящих в формулу. Формула, которая принимает значение истина на всех интерпретациях, называется тавтологией или тождественной единицей. Формула, имеющая значение ложь на всех интерпретациях, называется противоречием или тождественно ложная. Формула, имеющая значение истина хотя бы на 1 интерпретации, называется выполнимой. Формула, имеющая значение ложь хотя бы на одной интерпретации, называется опровержимой. Проверка, является ли эта формула тождественно истиной, ложной, выполнимой или опровержимой, осуществляется составлением таблицы истинностных значений. По существу, это проблема разрешимости в алгебре высказываний.

Логическое следствие A₁, A₂, A₃, A_n |- B.

Формула B является логическим следствием формул A₁, A₂, A₃,…,A_n, если она истина, когда все формулы A₁, A₂, A₃,…,A_n истины одновременно.

Теорема: формула B является логическим следствием формул A₁, A₂, A₃,…,A_n, если формула является тавтологией. (A₁A₂A₃…A_n B).

Эквивалентные преобразования формул: 1) АВВА 2) А(ВC)(AB)C

3) АААА; АААА 4) ¬(АВ)¬А¬В; ¬(АВ)¬А¬В 5) ААВА; А(АВ)А

6) АВА¬ВА; (АВ)(¬А¬В)А 7) А(ВС)АВАС; АВС(АВ)(АС)

8) АВ¬АВ 9) АВ(АВ)(ВА); АВ(¬АВ)(¬ВА)

10) А¬А0; А00; А1A; А¬А1; А0A; А11.

8. Логический вывод. Средства вывода в исчислении высказываний. Примеры вывода.

Под исчислением понимается некая формальная система, порождающая объект с заданными свойствами. В исчисление высказываний он порождается истинной формулой.

Любое исчисление строится из следующих компонентов:

1. система аксиом;

2. правило вывода истинных формул из исходных:

   1. правило подстановки;

   2. правило modus ponens.

Набор аксиом может быть различен. К ним предъявлены требования: 1) система аксиом должна быть полной и непротиворечивой; 2) каждая аксиома должна быть независима.

Аксиомы Новикова:

1. A(BA)

2. A(BC)((AB)(AC))

3. ABA

4. ABB

5. AAB

6. BAB

7. (AB)((AC)(ABC))

8. (BA)((CA)(BCA))

9. (AB)(¬В¬А)

10. A¬¬A

11. ¬¬AA

Правило MP: (А, АВ)/В

S_x/S_y – правило подстановки (если истина для х, то истина и для у).

Пример: |-KM((CD)KM)

A(BA)|A//KMKM((CD)KM)|B//CD

|-KM((CD)KM)

|-AA

1. Если A(BC)((AB)(AC)), вместо C подставить A, вместо B подставить (AA), то

(A((AA)A))((A(AA))(AA))

2. Если A(BA) и вместо B подставить (AA), то A((AA)A)

3. Из 1,2 по MP (A(AA))(AA)

4. Если A(BA) и вместо B подставить A, то A(AA)

5. Из 3,4 по MP AA

9. Логика предикатов. Язык логики предикатов. Эквивалентные преобразования предложений логики предикатов. Связь с предложениями Хорна логических программ.

Предикатом P(x₁,…,x_m), заданным на множестве M, называется функция, отображающая множество наборов значений переменных x₁,…,x_m в множестве {1, 0}. x₁,…,x_m - предметные переменные. Каждая из них может быть заданна на своём множестве. В отличии от высказывания предикат рассматривает свойства и отношения некоторой предметной области, то есть предикат позволяет проникнуть во внутрь высказывания. Можно сказать, предикат – переменная высказывания, высказывание – частный случай предиката. Число предметных переменных называется местностью предиката. P=2>3–высказывание, P(x)=x>3–одноместный предикат (свойство), P(x,y)=x>y–двуместный (отношение). Предметные переменные могут находиться под законом квантора – всеобщности () и существования (). Применение кванторов к предикатам называется операцией квантификации. Предикат не зависти от переменной под знаком квантора. Каждый квантор понижает местность предиката на 1. Основным средством формализации является понятие формулы. P(x,y)yR(y)zkQ(z,k,y).

Формула строится: 1) а, b— символы константы 2) x, y – предметные переменные

3. Pj,Qi – предикаты 4) () 5) ,,,,,, 6) f – функциональные символы

Формулы логики предикатов: 1) P,A – формула 2) P(x) – формула

3) Если P(x) и R(x) – формулы, то P(x) – формула, P(x)R(x) – формула и т.д.

Формула, принимающая значение истина хотя бы на 1 наборе значений переменных из исходного множества, называется выполнимой.

Формула, принимающая значение истина на всех наборах значений переменных, называется тавтологией. Формула, принимающая значение ложь на всевозможных наборах значений переменных, называется противоречием. Формула, принимающая значение истина на всевозможных наборах значений переменных, называется тождественной истинной в логике предикатов. P(x)=(sin²(x)+cos²(x)=1) на R, (x P(x,y))x P(x,y) – в логике предикатов.

Связанная переменная – находящаяся под знаком квантора. Свободная - не находящаяся.

Формулы, в которых нет одноименных свободных и связанных переменных, а также нет переменных, находящихся под знаком кванторов  и  одновременно называются формулами со свойством чистоты предметных переменных. Произвольную формулу логики предикатов можно привести к формуле со свойствами частоты предметных переменных операцией переименования предметных переменных. x P(x)R(x,y) x P(x)R(z,y)

Интерпретация формул логики предикатов – это последовательность действий:

• приписывание предметным константам конкретных значений из некоторого множества;

• приписывание предметных переменных некоторому множеству значений;

• приписывание функциональным символам конкретных функций;

• приписывание предикатным символам конкретных предикатов.

Эквивалентные формулы логики предикатов:

1. все эквивалентности логики высказываний имеют место в логике предикатов;

2. x (AB(x))Ax; x (AB(x))Ax, где A не зависит от x

3. x (AB(x))Ax; x (AB(x))Ax

4. x (A(x)B(x))x A(x)x B(x); x (A(x)B(x))x A(x)x B(x)

5. (xyz R(x,y,z))xyzR(x,y,z)

6. xyR(x,y)yxR(x,y); xyR(x,y)yxR(x,y) 7) x P(x)y P(y)

Формулы логики предикатов, не содержащие операций ,, групповых операций предикатов, находится в нормальной форме и не содержит отрицаний над кванторами.

Теорема: произвольную формулу логики предикатов можно привести к нормальной форме с помощью эквивалентных преобразований.

Пример:(xP(x)R(x,y)Q(x,y,z))((xP(x))R(x,y)Q(x,y,z))xP(x)(R(x,y)Q(x,y,z))

Формула, находящаяся в нормальной форме и имеющая вид Qx₁, Qx₂,…,Qx_n P(x), где Q(x_i) – кванторы  или , P(x) предикаты без кванторов, называется предварённой нормальной формой.

Клозы: father(misha,grisha). - факт; grandfather(X,Y):-father(X,Z), parent(Z,Y). – правило.

10. Исчисление предикатов. Средства вывода в исчислении предикатов.

Базируется на формулах логики предикатов и исчисления высказываний. Языком формализации является формула логики предикатов. Исчисление логики предикатов по аналогии с исчислением высказываний строится из систем аксиом и правил вывода.

Аксиомы: 1) A(BA) 2) A(BC)((AB)(AC)) 3) ABA 4) ABB

4. AAB 6) BAB 7) (AB)((AC)(ABC)) 8) (BA)((CA)(BCA))

9. (AB)(¬В¬А) 10) A¬¬A 11) ¬¬AA 12)x F(x)F(a) 13) F(a)x F(x).

Правила вывода: 1)(А,АВ)/В-MP;2)S_x/S_y–правило подстановки (если истина для х, то истина и для у); 3) (BA(x))/(Bx A(x)); 4) (A(x)B)/(x A(x)B).

11. Семантические сети. Явные и неявные зависимости в сетях. Пример применения семантических сетей для логических программ. Фреймы. Протофреймы и экзофреймы. Классы фреймов. Пример описания задач с помощью фреймов. Связь фреймов с клозами Хорна.

Семантическая сеть - это ориентированный граф с помеченными дугами и вершинами, отображающий объекты, свойства и отношения заданной предметной области.

Семантическая сеть может быть использована для графического представления знаний. В общем случае вершинами семантической сети могут быть: переменные, константы, функции, сети, фреймы. Формально сеть можно представить в виде тройки: S={V, R, F}, где V- множество вершин, R - множество связей между вершинами, F- множество отображений вершин друг в друга. Сеть даёт наглядное, но субъективное, а, следовательно, не однозначное представление о предметной области. В сети явно не рассматривается истиностно-ложностная интерпретация свойств объектов предметной области. Формализация знаний сетью не содержит правил эквивалентных преобразований. Сложное описание становится громоздким и необозримым. В этом случае целесообразно применять иерархическое многоуровневое описание. Существует гипотеза об универсальности семантической сети. Это означает возможность представления сетью любых связей о предметной области.

Пример формализации: слева от станка расположен приёмный бункер, расстояние до него 2 метра, справа от станка находится бункер готовой продукции, он находится рядом со станком. Робот перемещается параллельно станку и бункерам на расстоянии 1 метра.

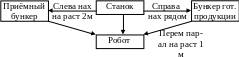
нах(пр. б., слева, станок) нах(пр. б., х, станок) роб(перем, пар, пр.б., станок, …)

father(petia, ania) sister(katia, tania) grandfather(petia, ira) :- father(petia, ania), mother(ania, ira)

grandfather(X, ira) – запрос. X=petia.

Фреймы - это структуры данных (некая формальная система), в которой в определенном порядке представлена информация о свойствах и отношениях объектов предметной области. Фреймы имеют более жёсткую унифицированную структуру и предикатную ориентацию. Фрейм можно представить в виде схемы, имеющей имя и список компонентов. Общий вид: имя фрагмента: <имя фрагмента >; <слот₁>=<значение₁>; <слот₂>=<значение₂>,…, <слот_n>=<значение_n>; <q₁, q₂, …,q_k> q_i- ссылки на другие фреймы. Фреймы могут быть с переменными (протофреймы) и со значениями (экзофреймы).

Пример: фрейм-резистор <резистор><тип-Х₁;точность-Х₂;жёсткость-Х₃>резистор>.

<Х₁=20кОм;…>. В общем случае в качестве слотов могут быть константы, переменные, функции, действия, процессы, другие фреймы. ИФР (Х₁, Х₂, Х₃)

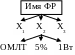
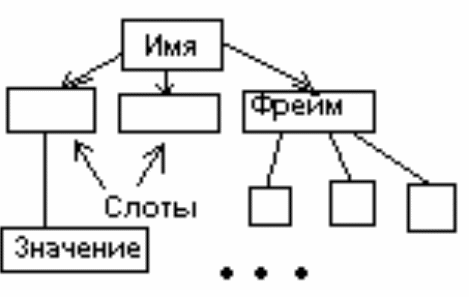
Пример: фрейм – взятие. Х₀ = робот , Х₁ = деталь, Х₂ = приёмный бункер, Х₃ = время, Х₄ = условие. Если в бункере есть деталь, то осуществлять действие.

domains k = integer s, n = real predicates summa( s, n, k )

clauses summa( S, N, K) :- K>0, K1 = K - 1, S1= S+N, summa( S1, N, K1).

summa( S, N, K) :- K=0, write( "сумма =", S).

Пусть n=5.6 , k=10. При запуске этой программы в окне ввода целей на запрос goal: вводится запрос summa(0, 5.6, 10) , где 0 -это начальное значение суммы, 5.6 -суммируемое число, а 10 - кратность суммирования. С помощью первого правила выполняется цикл суммирования, в результате которого вычисляется сумма. В конце цикла значение переменной К становится равной нулю, что делает истинным второе правило, с помощью которого выводится результат.