1.5. Застосування двійкових логічних елементів

Застосування двійкових ЛЕ.

В цифровій електроніці необхідно ЛЕ сформувати в схеми які носять назву комбінаційних логічних схем Ало комбінаційна логіка.

До комбінаційно-логічних схем відносять: шифратори, дешифратори, мультиплікатори, демультиплікатори та суматори. Є 3 основні способи вирішення значень символьної логіки:

• умовні позначення ЛЕ;

• таблиці істинності;

• Булеві вирази.

1. Конструювання схем на основі Булевих виразів

( або або рівні )

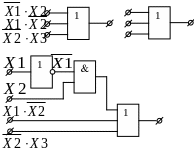
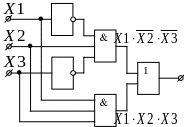
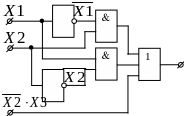
Булеві вирази зустрічаються в двох основних формах:

1. Сума добутків

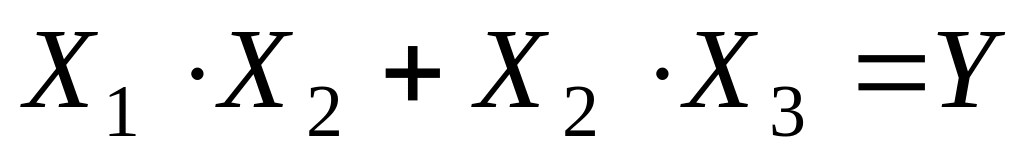
2. Добуток сум

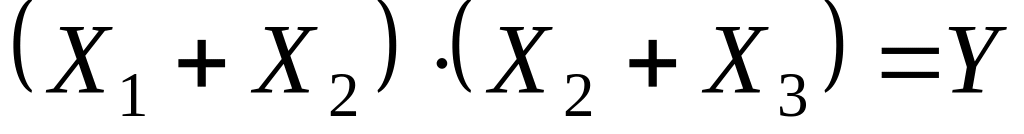
Друга форма називається кон’юктивною формою функції, а перша дизкон’юктивна форма.

Побудова схеми базового виразу на основі кон’юктивної форми функцій.

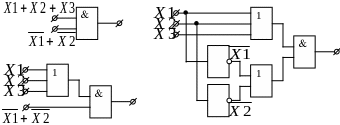
X1	X2	X3	Y
0	0	0	0
0	0	1	0
0	1	0	0
0	1	1	1
1	0	0	1
1	0	1	0
1	1	0	0
1	1	1	0

В першому випадку для дизкон’юктивної функції ми отримали “І-АБО”, а в другому випадку для кон’юктивної нормальної функції отримали «АБО-І».

Таблиці істинності для Булевих виразів.

І таблиці істинності і Булеві вирази є стислим описом (точний метод) роботи ЛЕ. Запишемо вирази для тих виразів в яких на вході має бути 1.

X1	X2	X3	Y
0	0	0	0
1	0	0	0
0	1	0	1
1	1	0	0
0	0	1	0
1	0	1	1
0	1	1	0
1	1	1	0

Зробимо з булевого виразу таблицю істиності

X1	X2	X3	Y
0	0	0	1
1	0	0	0
0	1	0	1
1	1	0	0
0	0	1	0
1	0	1	0
0	1	1	0
1	1	1	1

П

X1	X2	X3	Y
0	0	0	0
0	0	1	0
0	1	0	0
0	1	1	0
1	0	0	1
1	0	1	0
1	1	0	0
1	1	1	1

риклад вирішення логічної задачі