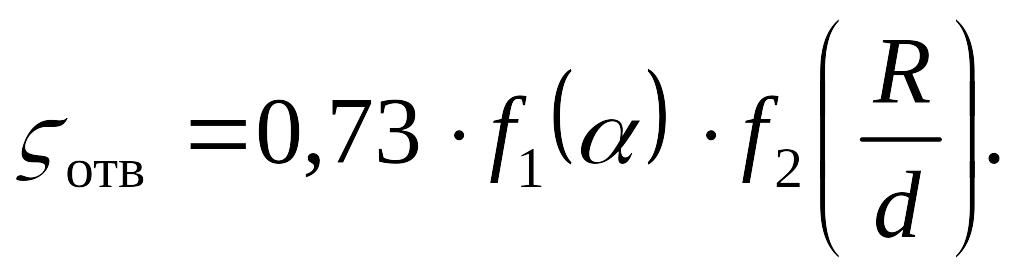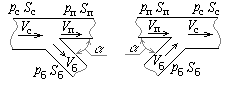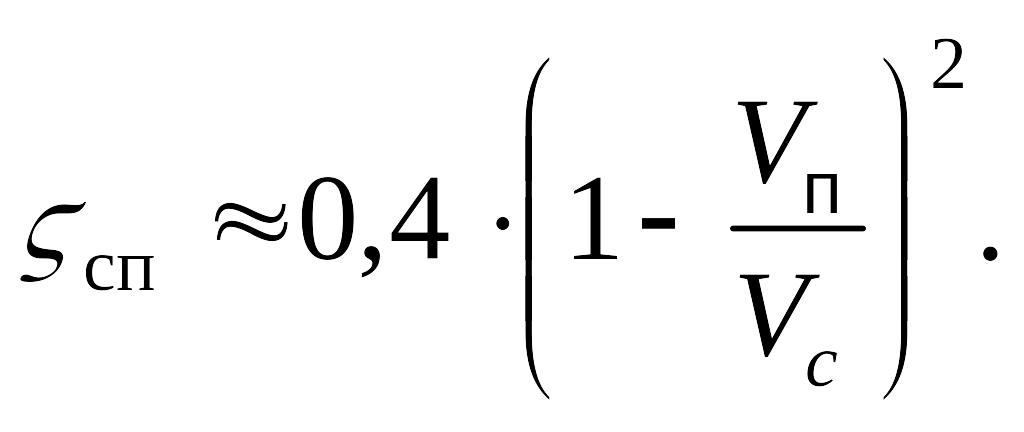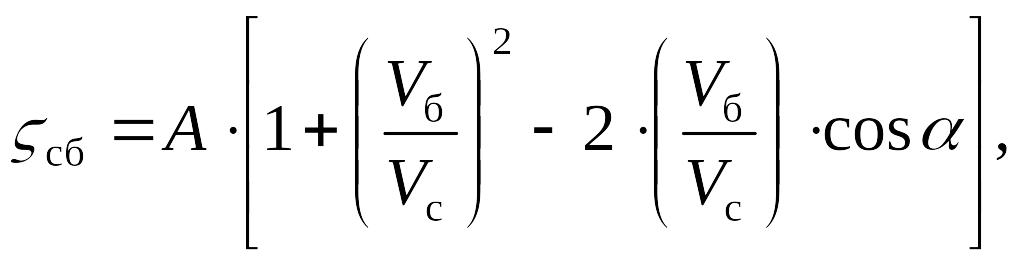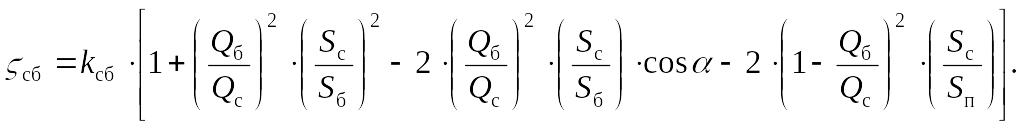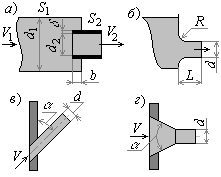
Вход потока в трубу

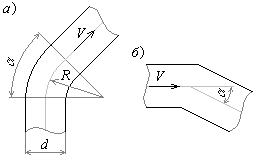
Рис. 1. Вход потока в трубу 1. Прямой вход при наличии сужения (рис. 1, а) без учета неравномерности профилей скорости: Коэффициент  определяют по приближенной формуле 2. Прямой вход при наличии коллектора радиусом R и торцевой стенки (рис.1, б) (Reавт = 104).   R/d 0 0,02 0,08 0,16 0,20  0,5 0,36 0,15 0,06 0,03   3. Косой вход в трубу без скругления (рис.  1, в) (Reавт = 104): 4. Прямой вход через конический коллектор (рис.  1, г). При  = 180˚ независимо от отношения h/D,  = 0,5. При  = 40–60˚ имеет наименьшее значение:   h/D 0,025 0,05 0,075 0,15 0,60 min 0,4 0,3 0,23 0,15 0,11

Изменение площади поперечного сечения потока без изменения направления течения

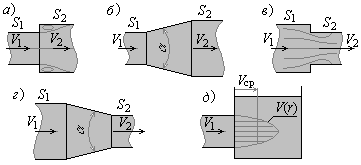
Рис. 2. Изменение площади сечения потока без изменения направления 1. Внезапное расширение (рис. 2, а). при Re > 104 а при Re < 104 2. Плавное расширение в диффузорах (рис. 2, б). Коэффициент потери давления в диффузоре   3. Внезапное сужение (рис. 2, в). 4. Плавное сужение (конфузор) (рис.  2, г). . Для углов сужения конических диффузоров (40–80)˚ с = 0,1–0,2. Ми­нимальными значениями коэффициента потери давления обладают кони­ческие конфузоры с углом при вершине 15–55˚; для них к = 0,04–0,05. 5. Выход потока из трубопровода (рис.  2, д):

Изменение направления потока

Изменение направления течения в трубопроводах осуществляется в отводах и коленах (рис. 3). Рис.  3. Изменение направления течения: а – отвод; б – колено   Для стандартных отводов постоянного сечения с углом  = 90˚ коэффициент потери давления можно принимать равным:   R/d 1 2 3 4 5 отв (гладкие) 0,29 0,23 0,23 0,26 0,29 отв (шероховатые) 0,54 0,38 0,34 0,36 0,38   Коэффициент потери давления в простом колене при Re > 2*105 (рис. 3, б) можно принимать равным нижеприведенным значениям в зависимости от угла поворота.   , о 15 30 45 60 90 кол 0,06 0,17 0,32 0,68 1,26

Узлы деления и слияния потоков
Рис.  4. Узлы деления и слияния потоков Коэффициент потери давления слияния сб оценивают по уравнению Коэффициент потери давления на ответвление сб оценивают по уравнению где А = 1,0 при Vб/Vс < 0,8 и А = 0,9 при Vб/Vс > 0,8. Коэффициент потерь давления на проход в магистральном канале при слиянии потоков определяют из выражения Коэффициент потерь давления потока, направленного из ответвления в магистральный канал, отнесенный к скорости в сечении после слияния, определяют по формуле Значения kсб находятся в пределах 0,6–1,0. Для прямых тройников ( = 90˚) kсб находят в зависимости от отношения площадей Sб/Sс.   Sб/Sс 0–0,2 0,3–0,4 0,6 0,8 1,0 kсб 1,0 0,75 0,70 0,65 0,60
Коэффициенты истечения из насадков Значения коэффициентов местных потерь давления для наиболее характерных групп элементов

Формула Шухова

Если на входе в газопровод температура газа Т₁ отличается от

наружной температуры Т_нар, то те­чение газа будет неизотермическим.

Полагая dx —> 0, получим

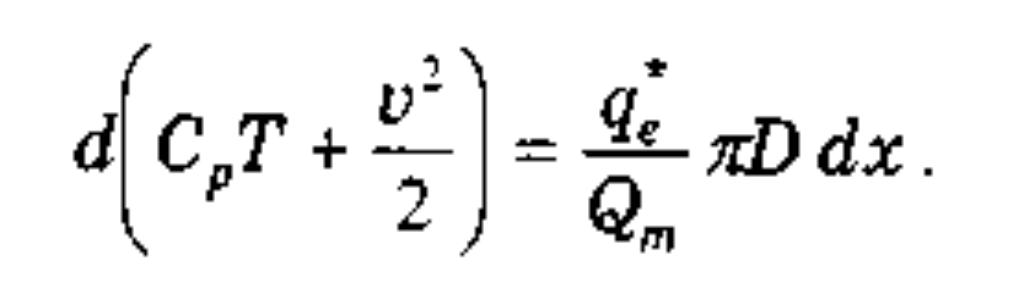
q*_e - тепло, подведенное в единицу времени через единицу площади поверхности - периметр газопровода можно представить в виде

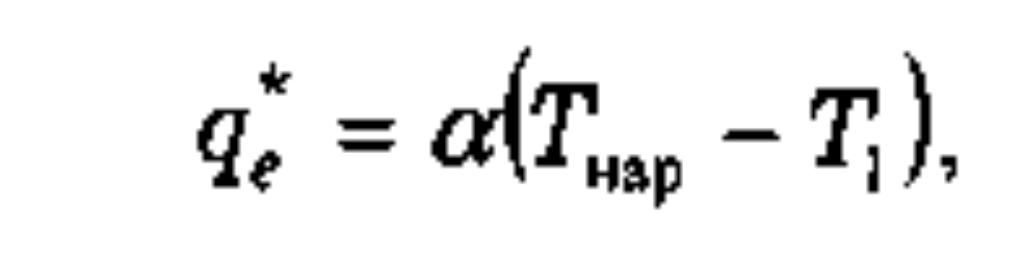
где а - коэффициент теплопередачи температура газа в газопроводе.

Пренебрегая изменением скоростного напора по длине газопровода имеем

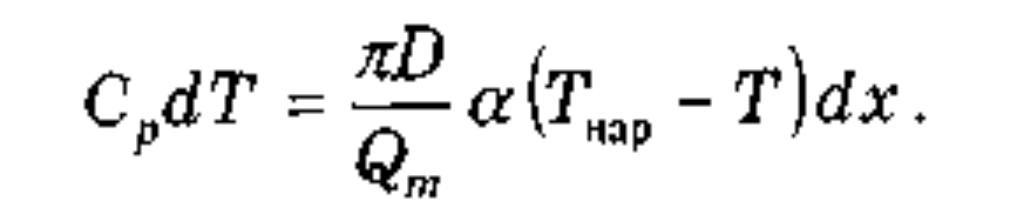
Интегрируя соотношение, при условии, что в начале трубо­провода при

х = 0 Т = Т₁ получим

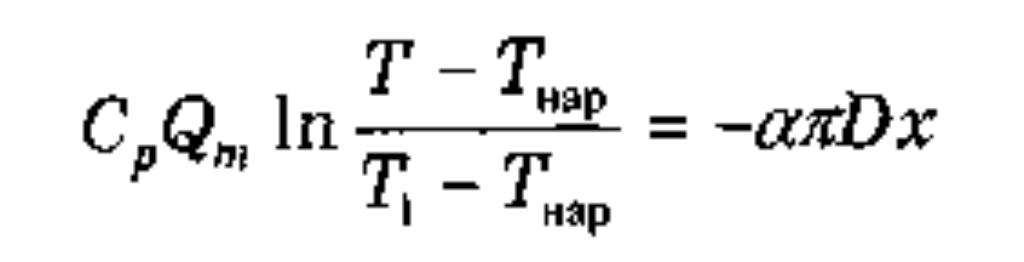
или

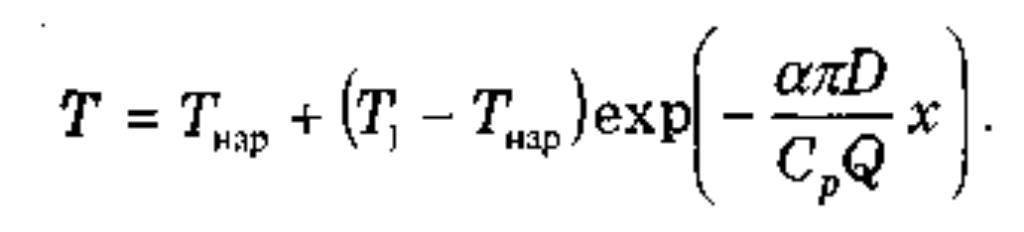
формула В.Г. Шу­хова оказыва­ется вполне точной для идеального газа, движущегося в трубе с дозвуко­вой скоростью.

Отсюда следует, что Т --> Т_нар при х --> ∞. Значение х = х₁, при котором температура газа в трубопроводе отличается от Т_нар меньше, чем на 1%, и определяется по формуле в виде

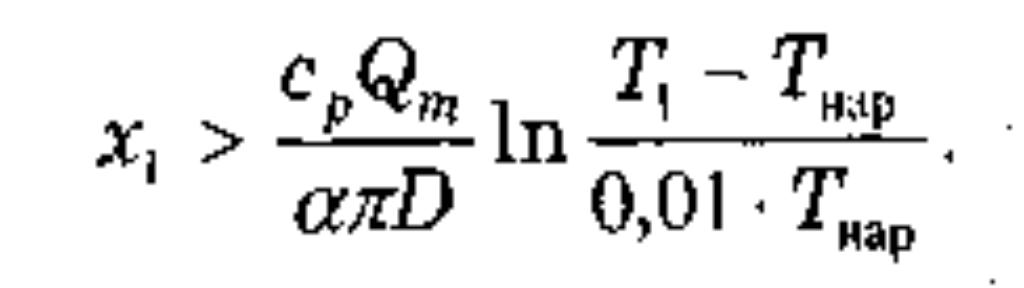
Оценки, выполненные по этой формуле, показывают, что величина x достаточно мала, то есть течение в магистральном газопроводе можно счи­тать изотермическим.

Законы сохранения массы и энергии при движении газа. Расчет газопровода

Уравнение состояния газа (уравнение Клайперона)

Массовый расход

Q_м = υ₁ ρ₁ s₁ = υ₂ ρ₂ s₂ = … …=υ_i ρ_i s_i = CONST

закон сохранения энергии (политропный процесс) для единицы веса газа:

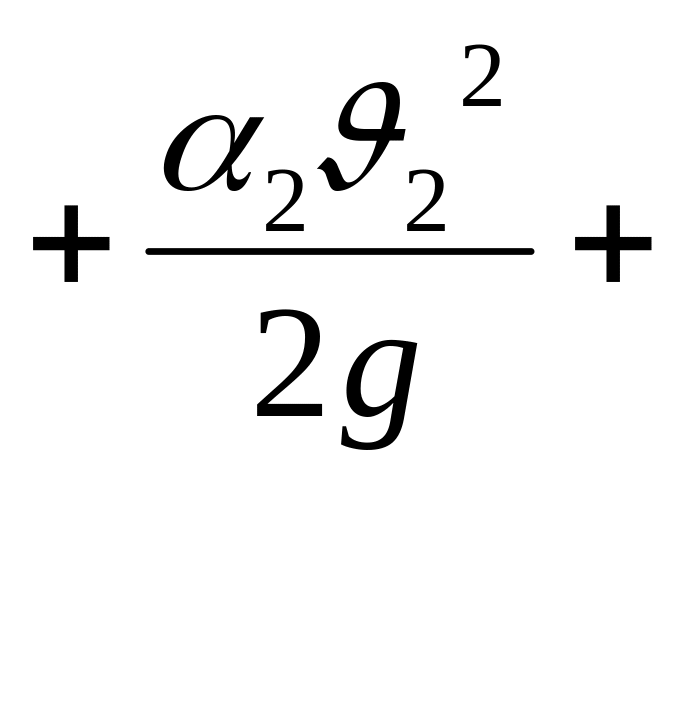Z₁ =Z₂ ^h_1-2

Z – удельная потенциальная энергия положения;

- удельная потенциальная энергия давления;

P / (ρg (n-1)) = RT / (g (n-1)) – внутренняя энергия;

- удельная кинетическая энергия;

ɑ - коэффициент Кориолиса (корректив кинетической энергии)

при ламинарном режиме ɑ = 2

при турбулентном режиме ɑ = 1,1 – 1,2, для практических расчетов при турбулентном режиме принимают ɑ = 1

h_1-2 = h_дл + h_м – суммарные потери энергии (потери по длине и местные

потери);

n – показатель политропы.

Уравнение Бернулли при изотермическом течении газа:

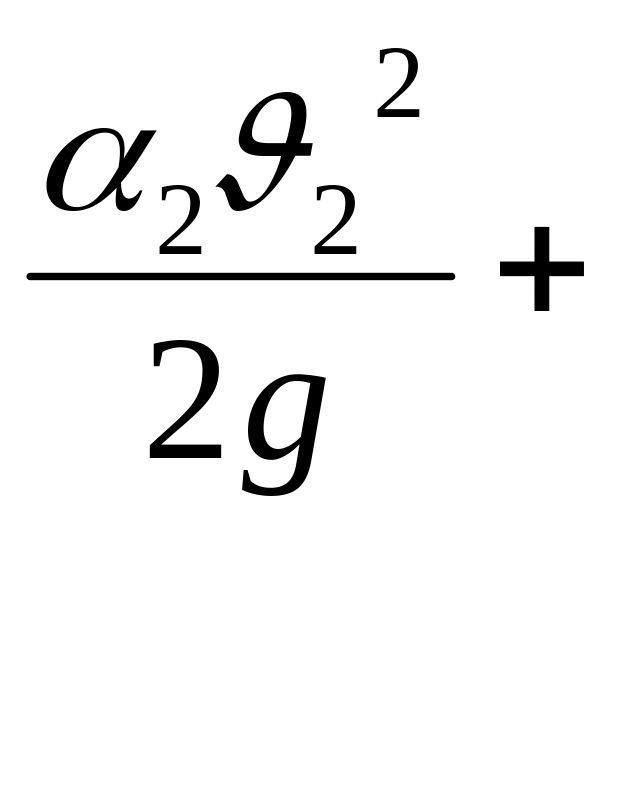Z₁ =Z₂ ^h_1-2

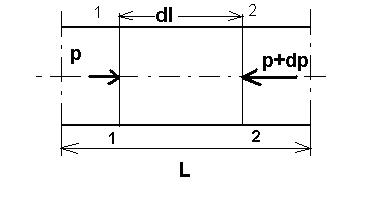
Схема к выводу расчетных зависимостей при движении газа

Уравнение Бернулли для выделенного элемента:

dh_дл

-dР = ρ g dh_дл = ρ λ (dl/d) υ²/2

Коэффициент трения

λ=ƒ(Re, ∆/d)

при ламинарном режиме

при турбулентном режиме

λ = 0,11 (68/Re+ ∆/d )^0.25

= 4 Qρ / d μ =4 Q_м/ π d µ= CONST

ρυ² =ρQ² _м /ρs² = Q² _м /s² = Q² _м Р₁ /ρ₁Р s²

Р /ρ = Р₁ /ρ₁ = RT = CONST

-dР = ρ λ (dl/d) υ²/2 = λ (dl/d) (Q²_мР₁ / 2 ρ₁Р s²)

Определение давления при известном расходе

Р₁ - Р₂ = λ (l/d⁵) (16 Q²_мР₁ / ρ₁π²)

Определение массового расхода при известных давлениях Р₁ и Р₂

Q_м = ((Р²₁ – Р²₂) ρ₁π² d⁵ / 16 λ l Р₁ )^0,5

Физические и теплофизические свойства природных газов.

Вязкость

Для расчета динамической вязкости природных газов m следует использовать соотношения Тодоса, которые в зависимости от величины приведённой плотности r_пр=r/r_кр имеют вид:

При r_пр> 2

При 0,3<r_пр£ 2

(в1)

При r_пр£ 0,3

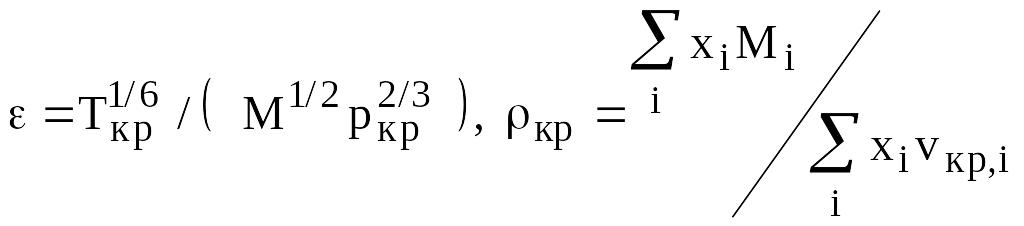
где

Коэффициент динамической вязкости m₀ при атмосферном давлении в зависимости от температуры рассчитывается по зависимостям:

при Т_пр³ 1,5

(в2)

при Т_пр< 1,5

В формулах (2), (3): р_кр - 0,1МПа, m - мкПа×с, Т - ^оК.

Для расчета вязкости в зависимости от температуры при атмосферном давлении можно использовать и следующие зависимости:

(в.3)

или

, (в3.1)

где t- ⁰С, h-м Па ^.с.

Погрешность расчетов по формулам (3.3), (3.3..1) при 12 £ М_см£100 и 283 £ Т£477 К не превышает 5%.

Порядок расчета m:

При содержании азота в природном газе более 5% следует учитывать его влияние на вязкость газа по правилу аддитивности:

, (в.4)

где у_а - молярная доля азота в составе смеси; m_а, m_у - коэффициенты динамической вязкости азота и углеводородной части, соответственно.

Коэффициент динамической вязкости углеводородного конденсата при различных давлениях и температурах приближенно можно рассчитать по эмпирической формуле Муталибова, Шубина и Абдурахманова:

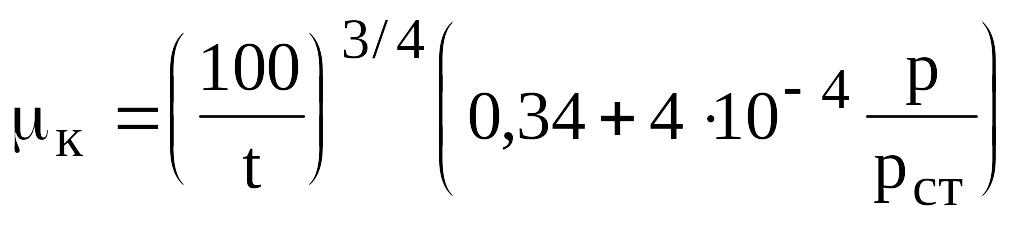, (в.5)

при 0,1 £ р£50,0 МПа и 30 £ t£200 ⁰C.

Теплоёмкость

При изобарическом процессе зависимость молярной теплоёмкости углеводородных компонентов природных газов при атмосферном давлении и различной температуре приближенно можно выразить следующим уравнением

, (в.6)

где t - температура, ⁰С;

M_i - молекулярная масса углеводорода, являющегося компонентом природного газа (от метана до гексана включительно).

Погрешность в интервале температур от -40 до +120⁰С: для СН₄ - С₅Н₁₂ – не более5%, для С₆Н₁₄-С₇Н₁₆ – не превышает 10%.

При изобарическом процессе молярная теплоёмкость неуглеводородных компонентов природных газов (азота, углекислого газа, сероводорода) равна примерно половине теплоёмкости углеводорода с одинаковой молекулярной массой при одной и той же температуре, которая рассчитывается по уравнению (7). Теплоёмкость смесей рассчитывается по правилу аддитивности

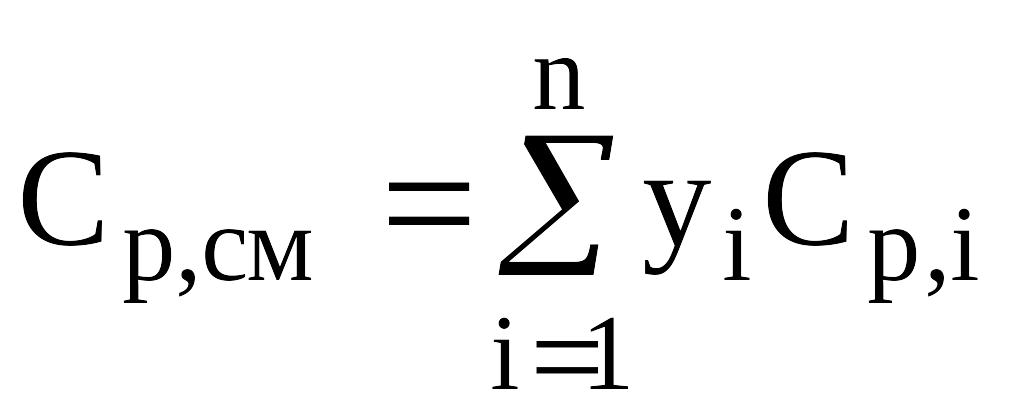, (в7)

где y_i - молярная доля i-го компонента в смеси;

С_р,i - молярная теплоёмкость i-го компонента.

Молярная теплоёмкость природных газов зависит от давления и температуры

, (в8)

где DС_р(р,t) - изотермическая поправка теплоёмкости на давление.

Поправка находится из графика по приведённым значениям давления и температуры или аналитически из уравнения состояния, например, Пенга-Робинсона

(в9)

Здесь:

(в10)

Для приближенных расчетов при 0,02 £ р_пр £ 4 и 1,3 £ Т_пр £ 2,5 поправку DС_р(р,t) можно рассчитать с погрешностью, не превышающей 10% по формуле

[кДж/(кмоль К)]. (в11)

При изобарическом процессе молярную теплоёмкость природного газа можно рассчитать и по формуле, предложенной Гухманом и Нагаревой

[кДж/(кмоль К)]. (в12)

Для расчета температуры и мощности в процессах адиабатного расширения и сжатия природных газов необходимо строго математически определить значения температурного К_Т и объёмного К_V коэффициентов адиабаты. Последнее возможно при определении частных производных коэффициента сверхсжимаемости соотношениями (1.30) и подстановкой их в зависимости:

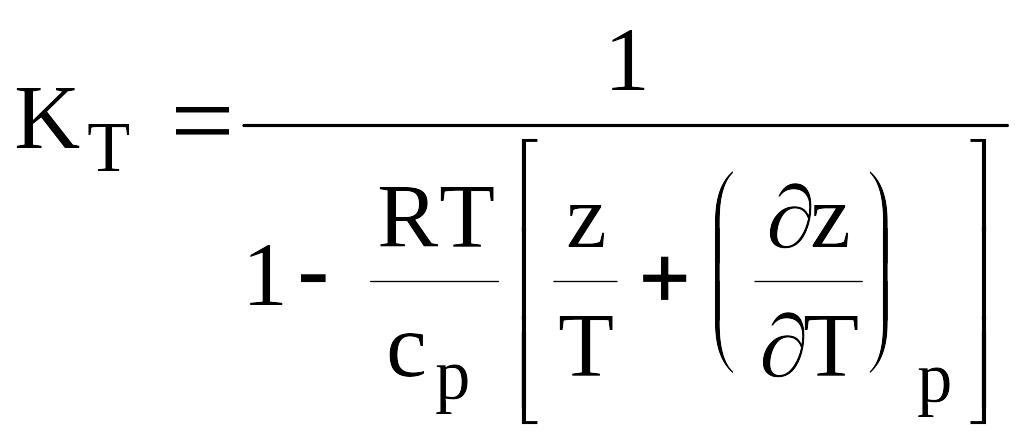, (в13)

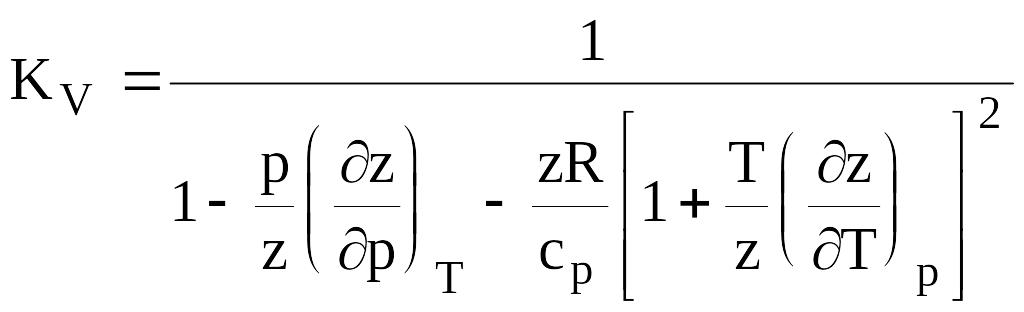, (в14)

Коэффициент адиабаты природного газа находится по формуле

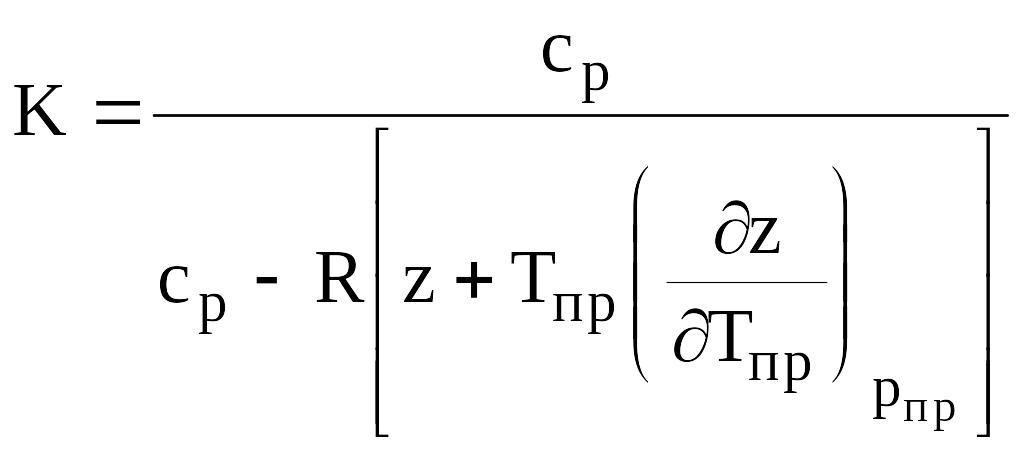(в15)

или используя аппроксимацию вычитаемого в знаменателе

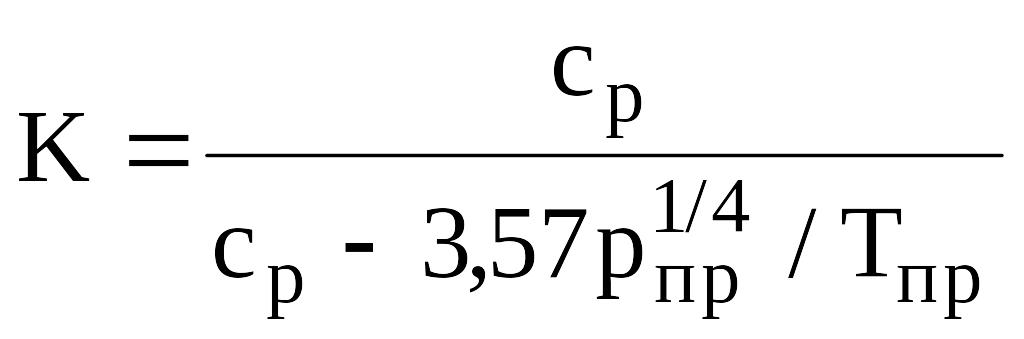(в16)

Если в расчетах необходимо иметь не молярную, а массовую теплоёмкость, то следует значение молярной теплоёмкости разделить на молекулярную массу газа М_i , т.е на массу киломоля i-го компонента, кг/моль.

Дросселирование газа. Коэффициент Джоуля-Томсона

Изменение температуры при снижении давления на 1 атм называется коэффициентом Джоуля - Томсона. Этот коэффициент изменяется в широких пределах и может быть положительным (охлаждение) или отрицательным (нагревание). Для природных газов коэффициент Джоуля - Томсона определяется из выражения

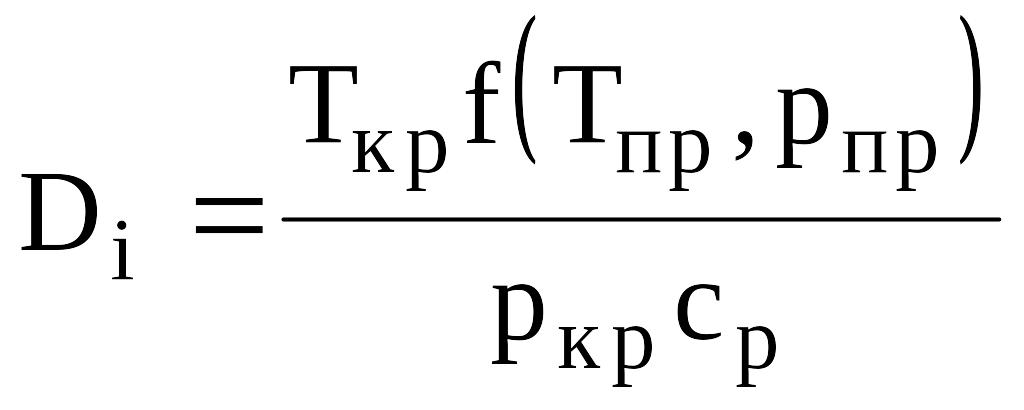, (в17)

где .

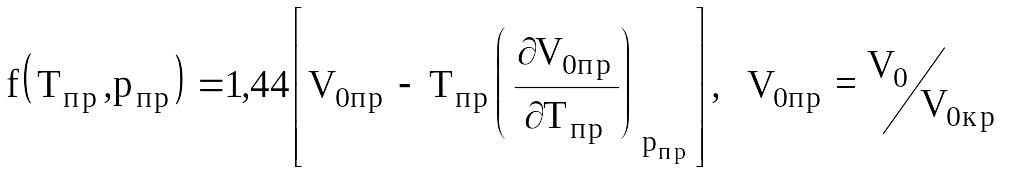Значение функции f можно определить по графику или рассчитать с погрешностью менее 7% по корреляции Гухмана и Нагарёвой

, (в18)

при 0,82 £ р_пр £ 3,5 и 1,6 £ Т_пр £ 2,1.

Для реальных природных газов коэффициент Джоуля-Томсона, кроме (в17) можно выразить через коэффициент сверхсжимаемости z:

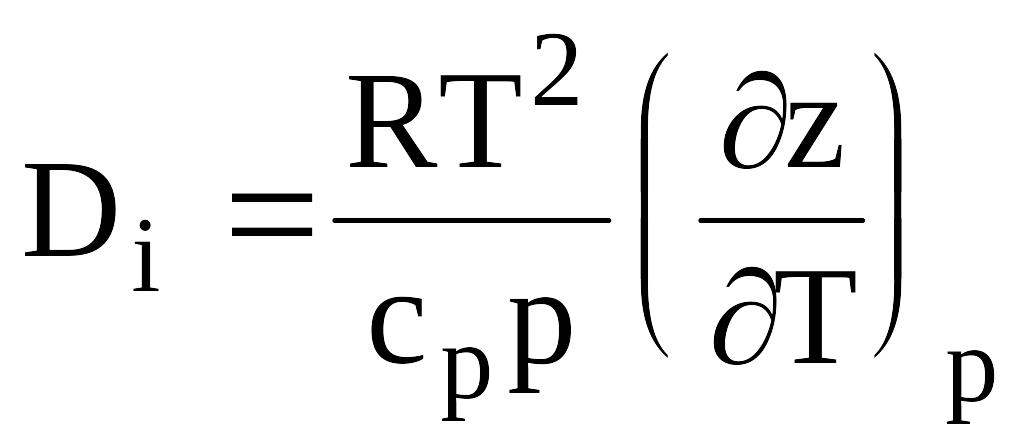. (в19)

Изменение температуры газа в процессе изоэнтальпийного расширения при значительном перепаде давления на дросселе называется интегральным дроссель-эффектом. Это изменение можно определить по соотношению

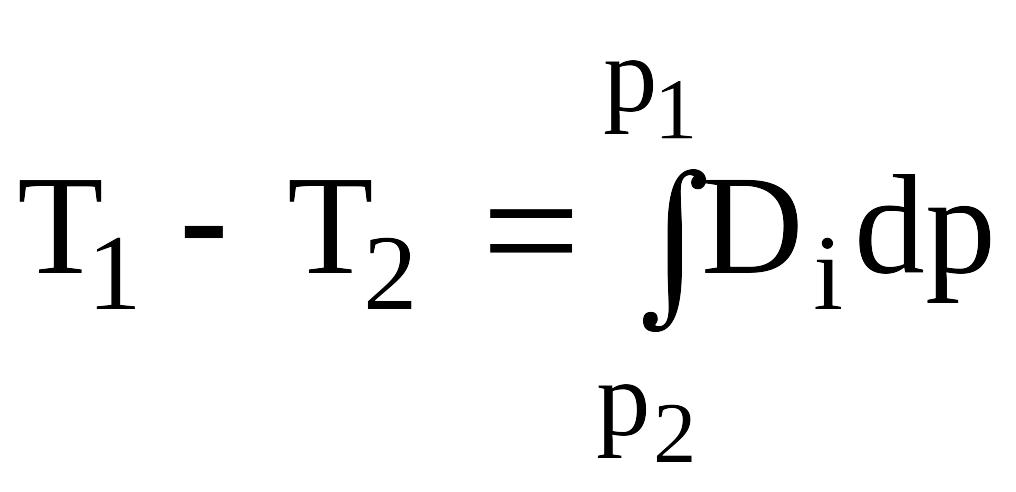(3.20)

или по энтальпийным диаграммам

Приближенно конечную температуру газа в процессе дросселирования находят по формуле

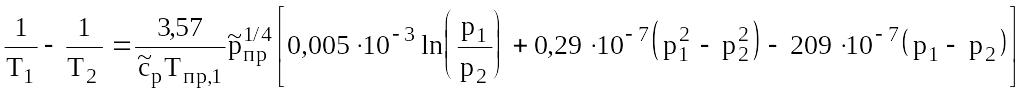, (в21)

где .

Интегральный коэффициент Джоуля-Томсона для природного газа изменяется от 2 до 4 К/МПа в зависимости от состава газа, падения давления и начальной температуры газа. Для приближенных расчетов среднее значение коэффициента Джоуля-Томсона можно принять равным 3 К/МПа.

Аналитические выражения частных производных от коэффициента сверхсжимаемости позволяют рассчитать изменение температур природных газов при изоэнтальпийном, изоэнтропийном и политропном процессах, т.е. изменение температур природных газов в процессе дросселирования, охлаждения и сжатия в идеальных детандере и компрессоре.

Дифференциальный коэффициент Джоуля-Томсона ( i =const)

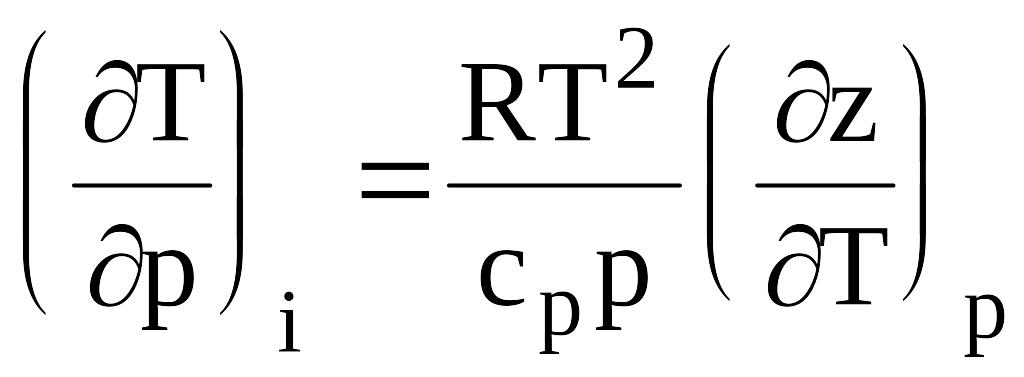. (в22)

Изменение температуры природного газа в идеальном детандере или компрессоре (S=const)

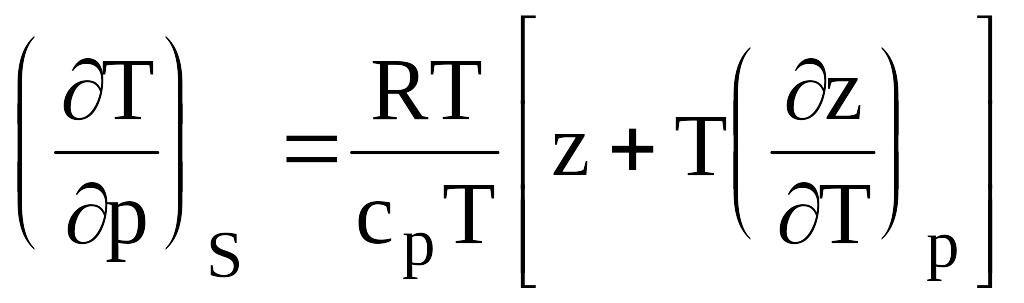. (в23)

Изменение температуры в политропном процессе (h=const)

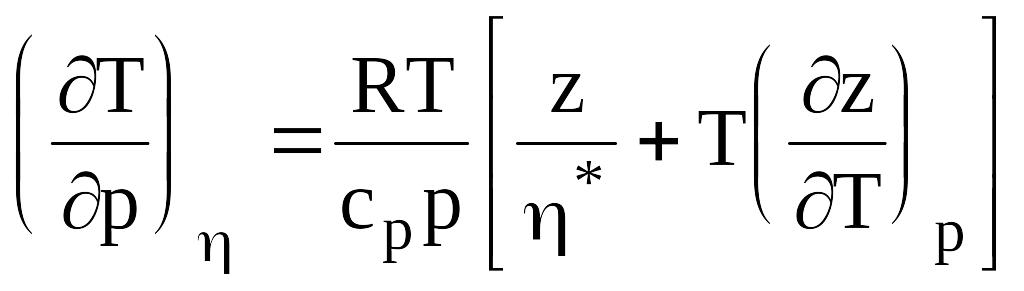, (в24)

где h^* - условный к.п.д. процесса (h^*<1 при сжатии газа в компрессоре и h^*>1 при расширении газа в детандере).

Эффективность использования свободного перепада давления для охлаждения газа в детандере по сравнению с дросселированием его в штуцере можно рассчитать по уравнению

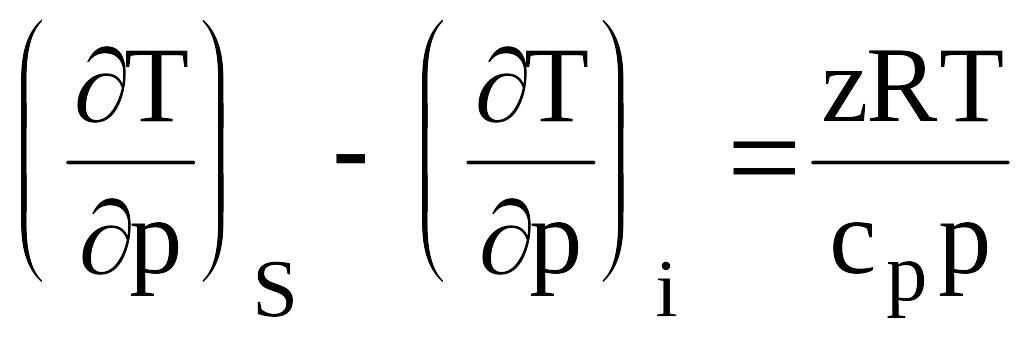. (в25)

Теплопроводность газов

Теплопроводность - физическое свойство вещества, определяющее скорость переноса теплоты и выражаемое уравнением Фурье

, (в26)

где dQ/dt - перенос теплоты посредством проводимости, Дж/с;

l - коэффициент теплопроводности вещества (теплопроводность) Вт/(м К);

А - площадь, перпендикулярная направлению потока тепла, м²;

х - расстояние, м;

Т - температура, К.

Теплопроводность природной газовой смеси можно определить по приведённой плотности r_пр=r/r_кр из зависимостей Стила -Тодоса и Тиракьяна.

Зависимости Стила-Тодоса:

а) r_пр> 2

b) 0,5<r_пр£ 2

(в.27)

3. r_пр£ 0,5

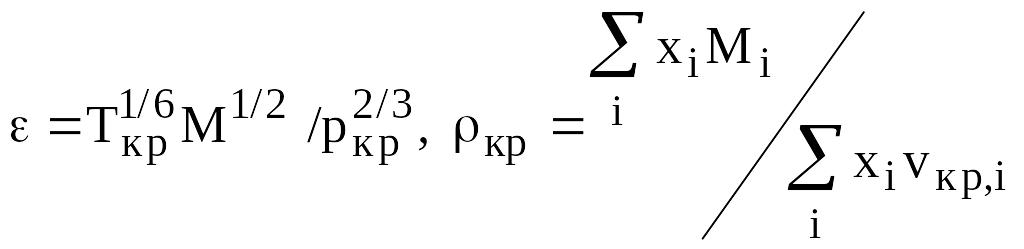
где l измеряется в 418.68 Вт/(м К).

Коэффициент теплопроводности l₀ при атмосферном давлении имеет следующую зависимость от температуры

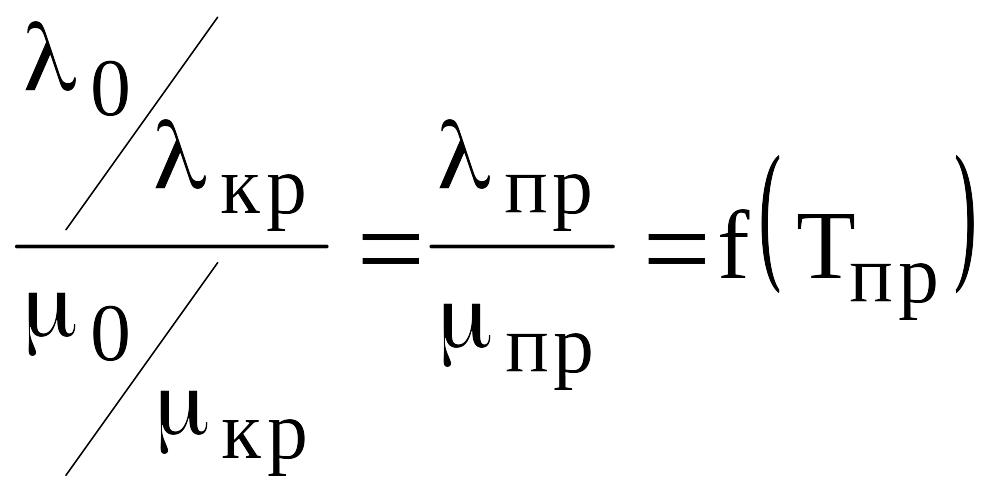, (в28)

где

Тпр	0,5	1,0	2,0	3,0	5,0	10,0	40,0
f	0,655	0,855	0,97	1,018	1,11	1,192	1,395

При Т_пр=0,8 - 8,0

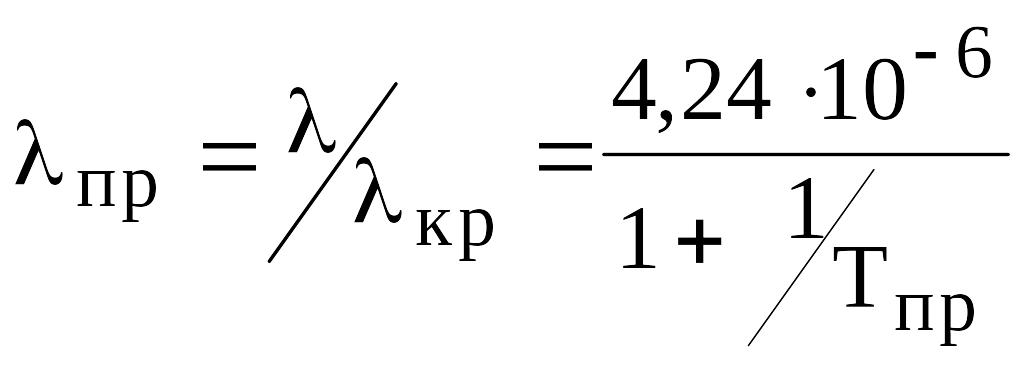. (в29)

Зависимость Тиракьяна

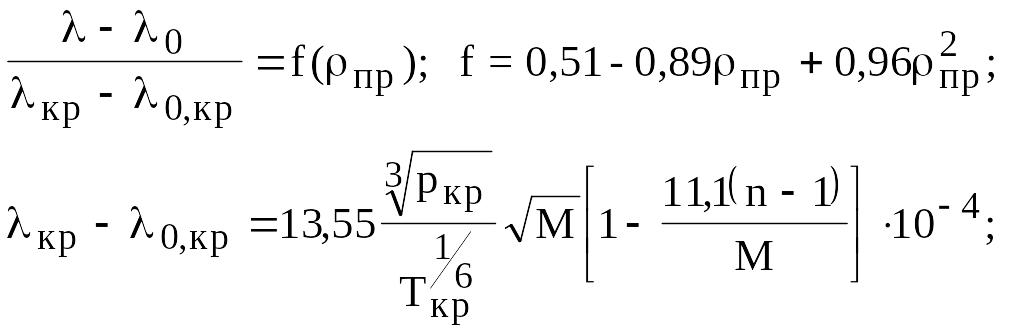(в30)

где n- число атомов углерода в молекулах; для смеси n=åx_in_i .
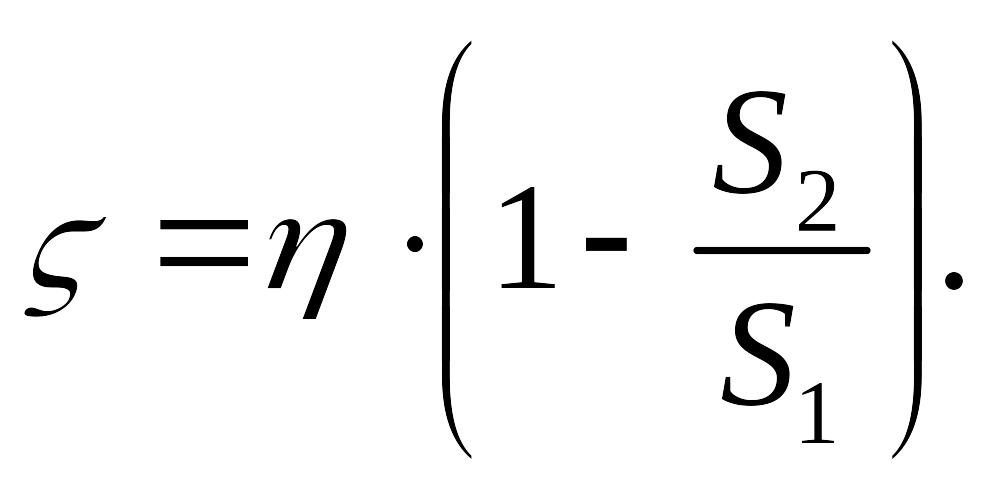
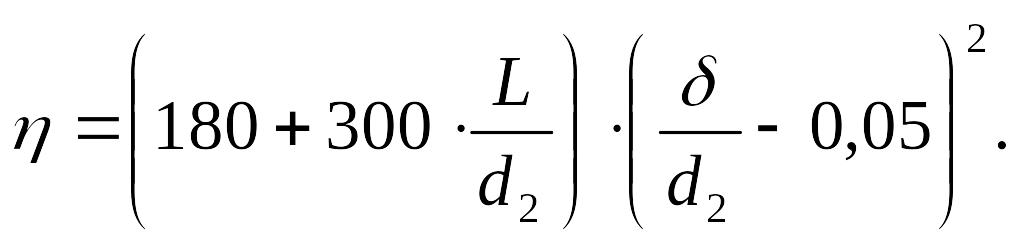
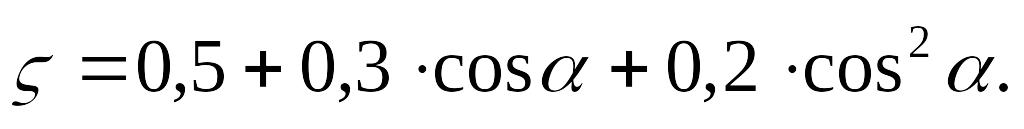
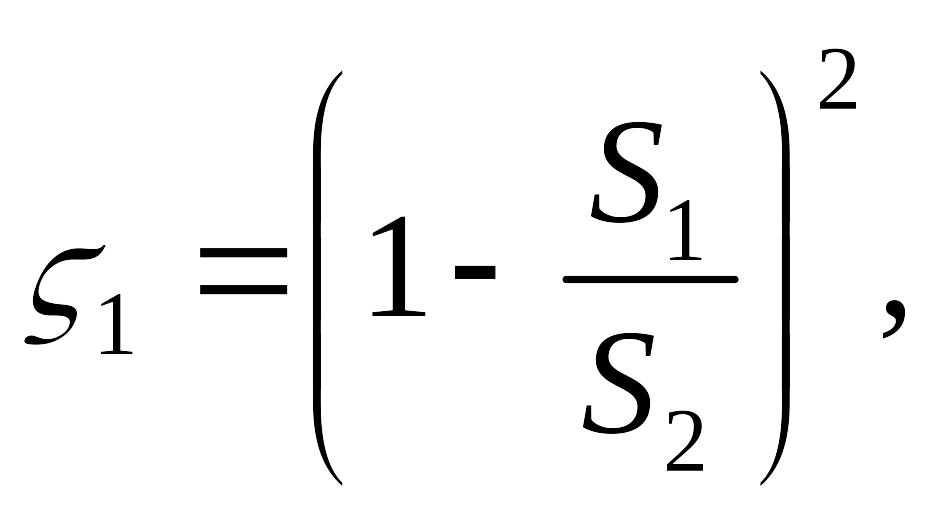
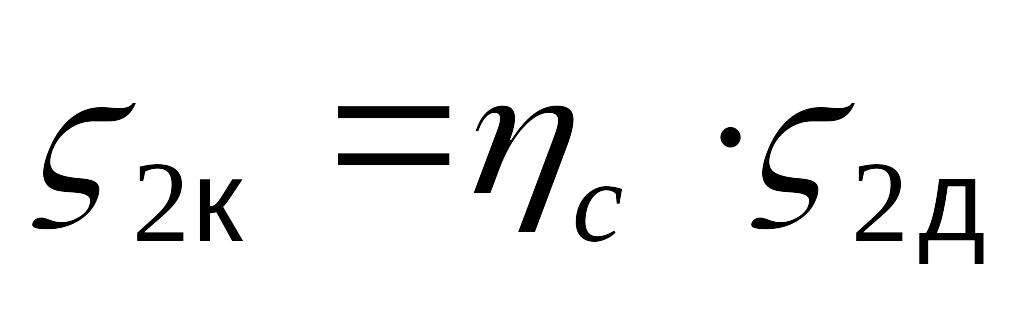