Лабораторная работа № 14

ОПРЕДЕЛЕНИЕ КОНЦЕНТРАЦИИ РАСТВОРА САХАРА С ПОМОЩЬЮ САХАРИМЕТРА СУ5 И ПОЛЯРИМЕТРА П161

Цель работы: Овладеть методикой определения концентрации сахара в растворах с помощью приборов, принцип работы которых основан на явлении вращения плоскости поляризации света.

Оборудование: 1. Сахариметр универсальный СУ-5.

2. Кювета КПС-30 (стеклянная).

3. Поляриметр П-161.

4. Две трубки с раствором сахара.

ТЕОРИЯ

В одноосном кристалле свет распространяется в направлении оптической оси так же, как и в изотропной среде, не давая двойного лучепреломления. Однако было замечено, что в кристаллах кварца распространение света вдоль оптической оси все же отличается от его распространения в изотропной среде. Оказалось, что в плоско-поляризованной волне, распространяющейся в кристалле кварца вдоль оптической оси, поворачивается плоскость поляризации. Впоследствии это явление было обнаружено в ряде других кристаллов и в некоторых жидкостях и получило название: вращение плоскости поляризации.

Вещества, вращающие плоскость поляризации, называются оптически активными.

Явление вращения плоскости поляризации (плоскости колебания вектора Е) в кварце было открыто Араго в 1811 г.

Параллельный пучок света, проходя через поляроид N₁ (поляризатор) и светофильтр F, (рис. 1), падал на пластинку кристаллического кварца Q, вырезанную перпендикулярно к оптической оси, так, что свет распространялся в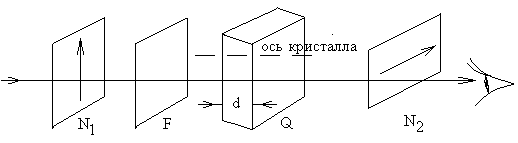 доль оси кварца.

Рис.1

Если второй поляроид N₂ (анализатор) был скрещен с первым, то свет все же проходил через эту систему. Только поворачивая ось анализатора N₂ на некоторый угол, можно добиться полного затемнения поля.

В этом опыте у линейно- (или плоско) поляризованного света после прохождения через кристалл кварца плоскость колебания вектора Е повернулась на некоторый угол, измеряемый углом поворота оси анализатора N₂. Меняя светофильтры, обнаружили, что угол поворота плоскости колебания вектора Е (плоскости поляризации) для разных длин волн различен, т.е. имеет место вращательная дисперсия.

Измерения, проведенные с разными фильтрами, показывают, что кварцевая пластинка толщиной 1 мм вращает плоскость поляризации на следующие углы:

для красного света  15;

для желтого света  21;

для зеленого света  27;

для синего света  33;

для фиолетового  51;

для ультрафиолетового  236.

Для каждой длины волны угол поворота плоскости поляризации пропорционален толщине пластинки.

Вращательную способность оптически активных твердых веществ характеризуют величиной угла , на который поворачивает плоскость поляризации пластинка толщиной 1 мм. Поэтому

 = d, (1)

где   угол поворота, d  толщина пластинки в мм,   коэффициент, зависящий от длины волны, природы вещества и температуры.

Наблюдения вращения плоскости поляризации в кварце показали, что существуют два сорта кварца: правовращающий, или положительный, дающий поворот плоскости поляризации вправо (по часовой стрелке), и левовращающий, или отрицательный (поворот против часовой стрелки). Величина угла вращения в обоих случаях одинакова (₊ = _).

В 1817 г. Френель показал, что явление вращения плоскости поляризации сводится к особому типу двойного лучепреломления. В основе рассуждений Френеля лежит гипотеза, согласно которой скорость распространения света в активных веществах различна для лучей, поляризованных по правому и левому кругу.

Правовращающее вещество. Левовращающее вещество.

υ_п > υ_л υ_п < υ_л

n_п < n_л n_п > n_л

(Индексы п  правый, л  левый).

Из механики известно, что плоское гармоническое колебательное движение можно разложить на два круговых, происходящих с той же частотой, но в противоположных направлениях.

П усть скорость линейно-поляризованного света направлена из-за листа на вас перпендикулярно листу в точке О (рис. 2). Тогда ОО^ представляет собой направление колебания вектора Е падающей на кристалл линейно-поляризованной волны.

Рис. 2

Возьмем произвольное значение вектора Е линейно поляризованной волны, падающей на кристалл, и разложим его на два вектора Е_п и Е_л , из которых первый вращается направо, а второй налево.

Если скорости распространения круговых колебаний одинаковые, то после того, как свет пройдет толщину кристалла d, круговые колебания Е_п и Е_л будут иметь одинаковые фазы и, следовательно, результирующее колебание будет совпадать в каждый момент с направлением ОО, т.е. поворота плоскости поляризации не произойдет (рис. 2 а).

Если скорости распространения круговых колебаний в кристалле разные, (пусть υ_п > υ_л ), то после того, как свет пройдет толщину кристалла d, круговые колебания Е_п и Е_л будут иметь разные фазы, длины волн «правых» и «левых» колебаний внутри кристалла будут разные.

и ;

Здесь _п и _л – длины волн в кристалле, соответствующие обоим видам колебания.

; , (2)

где   длина волны линейно-поляризованного света в вакууме.

Предположим, что толщина кварца d такова, что угол _п (см. рис. 2 б) кратен 2. Тогда вектор Е_п займет снова свое прежнее положение Е_п , вектор же Е_л, для которого _л  _п, займет некоторое новое положение Е_л. Новое положение вектора поляризации Е_л будет повернуто относительно старого на угол .

. (3)

Используя условие (2), получим:

. (4)

Найдем связь между углами  и .

Из рис. 2 б видно, что

_п   = _л +  , (5)

так как ОЕ  диагональ ромба ОЕ_л Е Е_п .

Из (5) видно, что _п  _л = 2 . (6)

С другой стороны,

 = _п  _{л .} (7)

Из (6) и (7) имеем, что  = 2 откуда

. (8)

Подставив в (8) выражение (4), получим:

. (9)

Таким образом, Френель показал, что угол поворота плоскости поляризации линейно-поляризованного света  возникает за счет разных коэффициентов преломления n_п и n_л волн, поляризованных по правому и левому кругу. Экспериментально величина этого угла  для оптически активных твердых веществ определяется по формуле (1).

Ф ренель проверил свою гипотезу, пропустив свет через сложную призму, склеенную из трех кусков кварца (рис. 3). Призмы 1 и 3 изготовлены из правовращающего, а призма 2 из левовращающего кварца. Все три призмы вырезаны так, что оптические оси параллельны их основаниям.

Рис. 3

При нормальном падении на систему призм плоско-поляризованного луча АВ этот луч войдет в первую призму без преломления. На границе же между первой и второй призмами он раздвоится, так как n_п  n_л. Еще более лучи разойдутся при преломлении на границе между второй и третьей призмами. В результате из призмы выйдут два луча D и D, причем оба будут поляризованы по кругу: один с правым, а другой с левым направлениями вращения. В действительности такие два поляризованные по кругу луча и были получены Френелем.

Наряду с кристаллами, существуют и жидкости, которые также обладают способностью вращать плоскость поляризации. К числу таких жидкостей принадлежат скипидар, водный раствор сахара, раствор виннокаменной кислоты. В 1831 г. Био опытным путем установил, что угол поворота плоскости поляризации  прямо пропорционален толщине d слоя раствора и прямо пропорционален концентрации С активного вещества:

 = dC (9)

Эта формула была получена на основании того, что для растворенных веществ величина вращения плоскости поляризации возрастает пропорционально числу молекул на пути луча света (пропорционально длине слоя и концентрации). Коэффициент пропорциональности  аналогично коэффициенту  для кристаллов, характеризует природу вещества и носит название постоянной вращения. Постоянная вращения зависит от длины волны и температуры, она может также меняться при изменении растворителя, и притом довольно сложным образом.

Наблюдается вращение плоскости поляризации и в аморфных телах, состоящих из тех же молекул (например, сахарные леденцы), и в парах соответствующих жидкостей (например, в парах скипидара). Опыт показывает, что постоянная вращения не зависит от агрегатного состояния. Так, для жидкой камфары (при 220К) найдено  = 7033 , а для парообразной (при 240К) =7031 .

Определив значение  для данного растворителя, определенной длины волны и температуры, можно использовать соотношение (9) для определения концентрации растворенного активного вещества.

Быстрота и надежность этого метода определения концентрации активных веществ сделали его основным методом количественных определений, практикуемых при производстве таких веществ как камфара, никотин и, особенно, сахаристые вещества (в медицине и сахарной промышленности). Измерения, выполняемые по определенным международным инструкциям, являются общепризнанными официальными контрольными приемами. В соответствии с этим, приборы, предназначенные для таких измерений и получившие название поляриметров или сахариметров (если они проградуированы в единицах концентрации сахара), доведены до высокой степени совершенства.