3.Средняя геометрическая

3.1 Средняя геометрическая простая применяется для характеристики средних темпов роста в рядах динамики с равноотстоящими уровнями и исчисляется по формуле:

где Х_i - цепной коэффициент роста уровня ряда динамики.

n – число цепных коэффициентов роста в ряду динамики.

3.2 Средняя геометрическая взвешенная применяется для характеристики средних темпов роста в рядах динамики с неравноотстоящими уровнями и исчисляется по формуле:

где f_i – промежуток времени между датами.

4. Средняя хронологическая

4.1 Средняя хронологическая простая

Средний уровень моментного ряда динамики с равноотстоящими уровнями характеризует средняя хронологическая простая, которая исчисляется по

формуле:

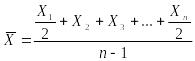
где X_i – значение уровня моментного ряда динамики;

n – число уровней моментного ряда динамики.

Например: По имеющимся данным определить средний товарный запас за первое полугодие

Дата	1 января	1 февраля	1 марта	1 апреля	1 мая	1 июня	1 июля
Товарный запас на указанную дату, тыс. руб.	984	1020	1003	998	1260	1254	1190
обозначение	X1	X2	X3	X4	X5	X6	X7

п=7

Средний товарный запас за полугодие составляет

4.2 Средняя хронологическая взвешенная

Средний уровень моментного ряда динамики с неравноотстоящими уровнями характеризует средняя хронологическая взвешенная, которая исчисляется по формуле:

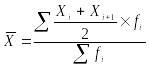
X_i и X_i+1 – значение уровня моментного ряда динамики и уровня, следующего за ним;.

где f_i – промежуток времени между датами.

Например: Известна списочная численность персонала организации на некоторые даты 2009 года. Определить среднесписочную численность персонала за год.

Дата	1.01.2009	1.03.2009	1.06.2009	1.09.2009	1.01.2010
Численность персонала по списку на указанную дату, чел.	1200	1100	1250	1500	1350

Среднесписочная численность персонала за 2009 год составляет

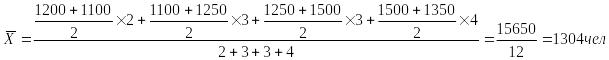
5. Средняя квадратическая

5.1 Средняя квадратическая простая применяется, когда возникает потребность расчета среднего размера признака, выраженного в квадратных единицах измерения, для несгруппированных данных. Она исчисляется как квадратный корнень из частного от деления суммы квадратов отдельных значений признака на их число по формуле:

.

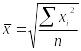где f_i – частота ряда распределения или удельный вес в совокупности.

5.2. Средняя квадратическая взвешенная применяется, когда возникает потребность расчета среднего размера признака, выраженного в квадратных единицах измерения, для сгруппированных данных. Исчисляется по формуле:

,

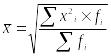где f_i – частота ряда распределения или удельный вес в совокупности.

6. Средняя кубическая

6.1 Средняя кубическая простая применяется, когда возникает потребность расчета среднего размера признака, выраженного в кубических единицах измерения, для несгруппированных данных. Исчисляется по формуле:

6.2 Средняя кубическая взвешенная применяется, когда возникает потребность расчета среднего размера признака, выраженного в кубических единицах измерения, для сгруппированных данных. Исчисляется по формуле:

.
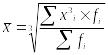