ПРАКТИЧЕСКОЕ ЗАНЯТИЕ №3.

Расчёт степенных средних величин.

Студент должен:

знать:

• область применения и методику расчёта степенных средних величин;

уметь:

• исчислять степенные средние величины;

• формулировать вывод по полученным результатам.

Методические указания

Средней величиной называется обобщающая величина статистической совокупности, выражающая типический уровень изучаемого признака. Она выражает величину признака, отнесённую к единице совокупности.

К степенным средним относятся средняя арифметическая, средняя гармоническая, средняя хронологическая, средняя геометрическая, средняя квадратическая, средняя кубическая.

Средняя величина всегда обобщает количественную вариацию признака, т. е. в средних величинах погашаются индивидуальные различия признака у отдельных единиц совокупности, обусловленные случайными обстоятельствами. Средняя величина позволяет сравнивать значения признака у единиц, относящихся к разным совокупностям.

Принципы применения средних величин:

1. Необходим обоснованный выбор признака у единиц совокупности, для которого рассчитывается средняя.

2. При определении средней величины в каждом конкретном случае следует исходить из качественного содержания осредняемого признака, учитывать взаимосвязь изучаемых признаков и особенность имеющихся исходных данных;

3. Средняя величина должна, прежде всего, рассчитываться по однородной совокупности. Однородную совокупность позволяет получить метод группировки.

4. Общие средние должны подкрепляться групповыми средними.

5. Средняя величина не может быть меньше минимального значения и больше максимального значения признака в совокупности.

Область применения и методика расчёта степенных средних величин:

1. Средняя арифметическая

1.1 Средняя арифметическая простая.

При небольшом объёме исходной информации, когда исходные данные не сгруппированы, применяется средняя арифметическая простая, которая рассчитывается по формуле:

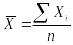
где ΣX_i - сумма значений;

n- число значений.

Например: В бригаде четверо рабочих в возрасте 21, 22, 23 и 24 года. Средний возраст рабочего бригады составляет

1.2 Средняя арифметическая взвешенная.

Когда исходные данные сгруппированы, то расчёт средней производится по

формуле средней арифметической взвешенной:

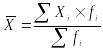
где f_i – частота ряда распределения, с которой отдельные варианты встречаются в совокупности (или удельный вес отдельных значений во всей совокупности).

Например: Рабочие бригады по возрасту распределились следующим образом:

Возраст рабочих, лет (X)	21	22	23	24
Численность рабочих, чел. (fi)	2	3	4	1

Средний возраст рабочего бригады составляет

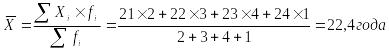
Если исходная информация представлена в виде интервального ряда распределения, то средняя арифметическая взвешенная определяется по формуле:

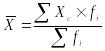
где X_c - центральное (серединное) значение признака в интервале.

Например: По имеющимся данным определить средний стаж рабочего бригады:

Стаж работы, лет	0 - 2	2 - 4	4 - 6	6 - 8	8 - 10
Численность рабочих, чел. (fi)	3	4	7	10	6

Для расчёта средней арифметической взвешенной интервального ряда распределения определим центральное (серединное) значение признака в каждом интервале. Среднее значение интервала находится как полусумма нижней границы данного интервала и нижней границы следующего интервала:

Стаж работы, лет	0 - 2	2 - 4	4 - 6	6 - 8	8 - 10
(Xc )

Оформим исходные данные а следующем виде:

Стаж работы, лет	0 - 2	2 - 4	4 - 6	6 - 8	8 - 10
(Xc )	1	3	5	7	9
Численность рабочих, чел. (fi)	3	4	7	10	6

Средний стаж рабочего бригады составляет

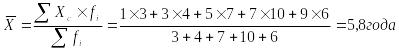
Если в интервальном ряду распределения имеются «открытые» интервалы, то для установления центральных (серединных) значений «открытых» интервалов на каждый из них условно распространяется величина смежного «закрытого» интервала.

Например: Работники организации по величине заработной платы за январь 2010 года распределились следующим образом:

Группы работающих по величине заработной платы за январь 2010 года, тыс.руб.	Численность работников, в % к итогу (fi)
До 9	10
9 - 12	24
12 - 15	40
15 - 20	20
20 и выше	6
Итого:	100

Определить по имеющимся данным среднюю зарплату работников организации.

Для расчёта средней арифметической взвешенной интервального ряда распределения определим центральное (серединное) значение признака в каждом интервале. На каждый открытый интервал условно распространим величину смежного закрытого интервала:

Группы работающих по величине заработной платы за январь 2010 года, тыс.руб.	Численность работников, в % к итогу (fi)	Центральное (серединное) значение интервала (Xc), руб
До 9	10
9 - 12	24
12 - 15	40
15 - 20	20
20 и выше	6
Итого:	100

Частоты при расчете средних арифметических могут быть выражены не только абсолютными величинами, но и относительными величинами – частостями Результаты применительно к одинаковым вариантам будут совпадать. В данном примере численность работников выражена не частотами, а частостями – удельными весами численности отдельных групп во всей совокупности, что не влияет на порядок расчёта средней.

Средняя зарплата работников организации составляет:

Необходимо небольшое пояснение применительно к расчету средней в интервальных рядах распределения. В действительности распределение отдельных вариантов в пределах интервала может оказаться неравномерным. В этом случае середина интервала будет в той или иной степени отличаться от фактической средней по интервалу. Это в свою очередь может повлиять на правильность общей средней, исчисленной по данным интервального ряда. Степень расхождения зависит от ряда причин. Во-первых, от числа вариант, чем больше число вариант, тем вероятнее, что середина интервала будет мало отличаться от групповой средней. Во-вторых, от величины интервала. Если интервал невелик, то ошибка будет незначительной, т.к. групповая средняя будет мало отличаться от середины интервала. В-третьих, от характера распределения. Чем симметричнее распределение, тем ошибка меньше. В-четвертых, размер ошибки зависит от принципа построения интервального ряда. При равных интервалах середина интервала будет ближе к средней по данной группе. При наличии открытых интервалов расхождение, как правило, взрастает из-за условного обозначения неизвестных границ. Общая средняя равна средней из частных (групповых) средних, взвешенных по численности соответствующих частей совокупности. Это правило имеет большое значение для всей статистики – организации сбора и обработки данных, их анализа.